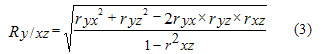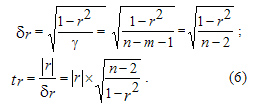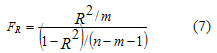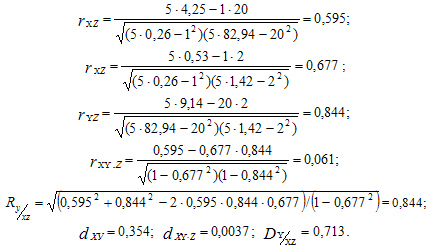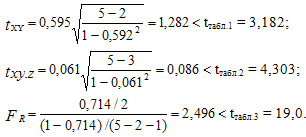Раздел 8. Корреляционно-регрессионный анализ

Общее представление о корреляционно-регрессивном анализе

Существующие между явлениями формы и виды связей весьма разнообразны по своей классификации. Предметом статистики являются только такие из них, которые имеют количественный характер и изучаются с помощью количественных методов. Рассмотрим метод корреляционно-регрессионного анализа, который является основным в изучении взаимосвязей явлений.

Данный метод содержит две свои составляющие части — корреляционный анализ и регрессионный анализ.Корреляционный анализ — это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами. Регрессионный анализ — это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами.

Для оценки силы связи в теории корреляции применяется шкала английского статистика Чеддока: слабая — от 0,1 до 0,3; умеренная — от 0,3 до 0,5; заметная — от 0,5 до 0,7; высокая — от 0,7 до 0,9; весьма высокая (сильная) — от 0,9 до 1,0. Она используется далее в примерах по теме.

 Данная корреляция характеризует линейную взаимосвязь в вариациях переменных. Она может быть парной (две коррелирующие переменные) или множественной (более двух переменных), прямой или обратной — положительной или отрицательной, когда переменные варьируют соответственно в одинаковых или разных направлениях.

Если переменные — количественные и равноценные в своих независимых наблюдениях  при их общем количестве , то важнейшими эмпирическими мерами тесноты их линейной взаимосвязи являются коэффициент прямой корреляции знаков австрийского психолога Г.Т.Фехнера (1801-1887) и коэффициенты парной, чистой (частной) и множественной (совокупной) корреляции английского статистика-биометрика К.Пирсона (1857-1936).

Коэффициент парной корреляции знаков Фехнера определяет согласованность направлений в индивидуальных отклонениях переменных  и  от своих средних  и . Он равен отношению разности сумм совпадающих () и несовпадающих () пар знаков в отклонениях  и  к сумме этих сумм:

Величина Кф изменяется от -1 до +1. Суммирование в (1) производится по наблюдениям, которые не указаны в суммах ради упрощения. Если какое-то одно отклонение  или , то оно не входит в расчет. Если же сразу оба отклонения нулевые: , то такой случай считается совпадающим по знакам и входит в состав . В таблице 12.1. показана подготовка данных для расчета (1).

Таблица 12.1 Данные для расчета коэффициента Фехнера.

По (1) имеем К_ф = (3 — 2)/(3 + 2) = 0,20. Направление взаимосвязи в вариациях !!Средняя численность работников|численности работников]] и объема товарооборота — положительное (прямолинейное): знаки в отклонениях и  и  в своем большинстве (в 3 случаях из 5) совпадают между собой. Теснота взаимосвязи переменных по шкале Чеддока — слабая.

Коэффициенты парной, чистой (частной) и множественной (совокупной) линейной корреляции Пирсона, в отличие от коэффициента Фехнера, учитывают не только знаки, но и величины отклонений переменных. Для их расчета используют разные методы. Так, согласно методу прямого счета по несгруппированным данным, коэффициент парной корреляции Пирсона имеет вид:

Этот коэффициент также изменяется от -1 до +1. При наличии нескольких переменных рассчитывается коэффициент множественной (совокупной) линейной корреляции Пирсона. Для трех переменных x, y, z он имеет вид

Этот коэффициент изменяется от 0 до 1. Если элиминировать (совсем исключить или зафиксировать на постоянном уровне) влияние  на  и , то их "общая" связь превратится в "чистую", образуя чистый (частный) коэффициент линейной корреляции Пирсона:

Этот коэффициент изменяется от -1 до +1. Квадраты коэффициентов корреляции (2)-(4) называются коэффициентами (индексами) детерминации — соответственно парной, чистой (частной), множественной (совокупной):

Каждый из коэффициентов детерминации изменяется от 0 до 1 и оценивает степень вариационной определенности в линейной взаимосвязи переменных, показывая долю вариации одной переменной (y), обусловленную вариацией другой (других) — x и y. Многомерный случай наличия более трех переменных здесь не рассматривается.

Согласно разработкам английского статистика Р.Э. Фишера (1890-1962), статистическая значимость парного и чистого (частного) коэффициентов корреляции Пирсона проверяется в случае нормальности их распределения, на основании -распределения английского статистика В.С. Госсета (псевдоним "Стьюдент"; 1876-1937) с заданным уровнем вероятностной значимости  и имеющейся степени свободы , где  — число связей (факторных переменных). Для парного коэффициента  имеем его среднеквадратическую ошибку  и фактическое значение -критерия Стьюдента:

Для чистого коэффициента корреляции  при расчете его  вместо (n-2) надо брать , т.к. в этом случае имеется m=2 (две факторные переменные x и z). При большом числе n>100 вместо (n-2) или (n-3) в (6) можно брать n, пренебрегая точностью расчета.

Если t_r > t_табл. , то коэффициент парной корреляции — общий или чистый является статистически значимым, а при t_r≤ t_табл. — незначимым.

Значимость коэффициента множественной корреляции R проверяется по F — критерию Фишера путем расчета его фактического значения

При F_R > F_табл. коэффициент R считается значимым с заданным уровнем значимости a и имеющихся степенях свободы  и , а при F_r≤ F_табл — незначимым.

В совокупностях большого объема n > 100 для оценки значимости всех коэффициентов Пирсона вместо критериев t и F применяется непосредственно нормальный закон распределения (табулированная функция Лапласа-Шеппарда).

Наконец, если коэффициенты Пирсона не подчиняются нормальному закону, то в качестве критерия их значимости используется Z — критерий Фишера, который здесь не рассматривается.

Условный пример расчета (2) — (7) дан в табл. 12.2, где взяты исходные данные табл.12.1 с добавлением к ним третьей переменной z — размера общей площади магазина (в 100 кв. м).

Таблица 12.2. Подготовка данных для расчета коэффициентов корреляции Пирсона

Согласно (2) — (5), коэффициенты линейной корреляции Пирсона равны:

Взаимосвязь переменных x и y является положительной, но не тесной, составляя по их парному коэффициенту корреляции величину  и по чистому — величину  и оценивалась по шкале Чеддока соответственно как "заметная" и "слабая".

Коэффициенты детерминации d_xy =0,354 и d_xy.z = 0,0037 свидетельствуют, что вариация у (товарооборота) обусловлена линейной вариацией x (численности работников) на 35,4% в их общей взаимосвязи и в чистой взаимосвязи — только на 0,37%. Такое положение обусловлено значительным влиянием на x и y третьей переменной z — занимаемой магазинами общей площади. Теснота ее взаимосвязи с ними составляет соответственно r_xz=0,677 и r_yz=0,844.

Коэффициент множественной (совокупной) корреляции трех переменных показывает, что теснота линейной взаимосвязиx и z c y составляет величину R = 0,844, оцениваясь по шкале Чеддока как "высокая", а коэффициент множественный детерминации — величину D=0,713, свидетельствуя, что 71,3 % всей вариации у (товарооборота) обусловлены совокупным воздействием на нее переменных x и z. Остальные 28,7% обусловлены воздействием на y других факторов или же криволинейной связью переменных y, x, z.

Для оценки значимости коэффициентов корреляции возьмем уровень значимости . По исходным данным имеем степени свободы  для  и  для . По теоретической таблице находим соответственно t_табл.1. = 3,182 и t_табл.2. = 4,303. Для F-критерия имеем и  и по таблице находим F_табл. = 19,0. Фактические значения каждого критерия по (6) и (7) равны:

Все расчетные критерии меньше своих табличных значений: все коэффициенты корреляции Пирсона статистически незначимы.