|
Математическая модель описывается (представляется) математическими структурами, математическим аппаратом (числа,
буквы, геометрические образы, отношения, алгебраические
структуры и т.д.).
У математических моделей есть и дидактические аспекты - развитие
модельного и математического стиля мышления, позволяющего вникать в структуру и
внутреннюю логику моделируемой системы.
Отметим основные операции (процедуры) математического моделирования.
1. Линеаризация. Пусть дана математическая модель М=М(X, Y, A), где X - множество входов, Y - множество выходов,
А - множество состояний системы. Схематически можно это
изобразить так: X->A->Y. Если X, Y, A - линейные пространства (множества), а 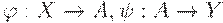 - линейные операторы (т.е. любые линейные комбинации ax+by
аргументов - линейные операторы (т.е. любые линейные комбинации ax+by
аргументов 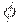 и и 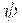 преобразуют в соответствующие линейные
комбинации преобразуют в соответствующие линейные
комбинации 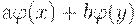 и и 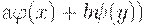 , то система (модель) называется линейной. Все другие системы (модели) - нелинейные. Они труднее поддаются
исследованию, хотя и более актуальны. Нелинейные модели
менее изучены, поэтому их часто линеаризуют - сводят к линейным
моделям каким-то образом, какой-то корректной линеаризующей процедурой. , то система (модель) называется линейной. Все другие системы (модели) - нелинейные. Они труднее поддаются
исследованию, хотя и более актуальны. Нелинейные модели
менее изучены, поэтому их часто линеаризуют - сводят к линейным
моделям каким-то образом, какой-то корректной линеаризующей процедурой.
Пример. Применим операцию линеаризации к
модели (какой физической системы, явления?) у=at2/2,
0<=t<=4, которая является нелинейной (квадратичной). Для этого заменим
один из множителей t на его среднее значение для
рассматриваемого промежутка, т.е. на t=2. Такая (пусть простят меня знакомые с линеаризацией читатели, - хоть и очень наглядная, но очень грубая!)
процедура линеаризации дает уже линейную
модель вида y=2at. Более точную линеаризацию можно
провести следующим образом: заменим множитель t не на
среднее, а на значение в некоторой точке (это точка -
неизвестная!); тогда, как следует из теоремы о среднем из курса высшей
математики, такая замена будет достаточно точна, но при этом необходимо оценить
значение неизвестной точки. На практике используются
достаточно точные и тонкие процедуры линеаризации.
2. Идентификация. Пусть М=М(X, Y, A), A={ai}, ai=(ai1, ai2, ..., aik) - вектор состояния объекта
(системы). Если вектор ai
зависит от некоторых неизвестных параметров, то задача идентификации
(модели, параметров модели) состоит в определении по
некоторым дополнительным условиям, например, экспериментальным данным,
характеризующим состояние, системы в некоторых случаях. Идентификация
- задача построения по результатам наблюдений
математических моделей некоторого типа, адекватно описывающих поведение
системы. Если S={s1, s2, ..., sn} -
некоторая последовательность сообщений, получаемых от источника информации о
системе, М={m1, m2, ..., mz} - последовательность
моделей, описывающих S, среди которых, возможно, содержится оптимальная (в
каком-то смысле) модель, то идентификация модели М
означает, что последовательность S позволяет различать (по
рассматриваемому критерию адекватности) две разные модели в М.
Последовательность сообщений (данных) S назовем информативной, если она
позволяет различать разные модели в М. Цель идентификации
- построение надежной, адекватной, эффективно функционирующей гибкой модели на
основе минимального объема информативной последовательности сообщений. Наиболее
часто используемые методы идентификации систем
(параметров систем): метод наименьших квадратов, метод
максимального правдоподобия, метод байесовских оценок, метод марковских цепных оценок, метод эвристик,
экспертное оценивание и другие.
Пример. Применим операцию идентификации
параметра a в модели предыдущего примера. Для этого необходимо задать
дополнительно значение y для
некоторого t, например, y=6 при t=3. Тогда из модели получаем: 6=9a/2,
a=12/9=4/3. Идентифицированный параметр
а определяет следующую модель y=2t2/3. Методы идентификации
моделей могут быть несоизмеримо сложнее, чем приведенный прием.
3. Оценка адекватности (точности) модели.
Пример. Оценим адекватность (точность) модели у=at2/2, 0<=t<=4, полученной в
результате линеаризации выше. В качестве меры (критерия)
адекватности рассмотрим привычную меру - абсолютное значение
разности между точным (если оно известно) значением и значением, полученным по модели (почему берется по модулю?).
Отклонение точной модели от линеаризованной
будет в рамках этого критерия равно |at2/2-2at|, 0<=t<=4. Если a>0,
то, как несложно оценить с помощью производной, эта погрешность
будет экстремальна при t=2a. Например, если a=1, то эта величина не превосходит
2. Это достаточно большое отклонение, и можно заключить, что наша
линеаризованная модель в данном случае не является адекватной (как исходной
системе, так и нелинеаризованной модели).
4. Оценка чувствительности модели (чувствительности к изменениям
входных параметров).
Пример. Из предыдущего примера следует, что чувствительность
модели у=at2/2, 0<=t<=4 такова, что изменение входного параметра t на 1%
приводит к изменению выходного параметра y на более,
чем 2%, т.е. эта модель является чувствительной.
5. Вычислительный
эксперимент по модели. Это эксперимент,
осуществляемый с помощью модели на ЭВМ с целью определения, прогноза тех или
иных состояний системы, реакции на те или иные входные
сигналы. Прибором эксперимента здесь является компьютер (и модель!). Это
процедура часто отождествляется с компьютерным моделированием.
Отметим основные причины, несколько тормозящие выход
математического моделирования на новые информационные
технологии:
·
традиционное описание модели
системами математических уравнений, соотношений; в то же время, большинство
плохо структурированных и плохо формализуемых систем описываются с помощью
экспертных данных, эвристических и имитационных процедур, интегрированных пакетов
программ, графических образов и т.д.;
·
существующие средства описания и
представление моделей на ЭВМ не учитывают специфику моделирования, нет единого
представления моделей, генерации новых моделей по банку моделей;
·
недооценка возможностей
компьютера, который может делать больше, чем простая реализация алгоритма, как
правило, структурируемого и/или реализуемого хорошо, отсутствие доступа к опыту
моделирования на ЭВМ.
В базовой пятерке: "система (исследуемая среда) - модель
(описание среды) - алгоритм (программа)
- компьютер (компьютерная технология) - пользователь (выработка решения)" при компьютерном
моделировании главную роль играют уже алгоритм (программа), компьютер и технология,
точнее, инструментальные системы для компьютера, компьютерные технологии.
Пример. При имитационном моделировании (при отсутствии строгого и
формально записанного алгоритма) главную роль играют технология и средства
моделирования; аналогичная ситуация наблюдается в когнитивной графике.
Модель не эквивалентна программе, а моделирование не сводится к программированию.
Специфические операции математического
моделирования, например, идентификация, линеаризация не сводятся в ЭВМ к преобразованию в ней
программ. Расширяется и область применения компьютера и компьютерных
моделей.
Основные функции компьютера при моделировании систем:
·
исполнение роли вспомогательного
средства для решения задач, доступных и для обычных вычислительных средств,
алгоритмам, технологиям;
·
исполнение роли средства постановки
и решения новых задач, не решаемых традиционными средствами, алгоритмами,
технологиями;
·
исполнение роли
средства конструирования компьютерных обучающих и моделирующих сред типа:
"обучаемый - компьютер - обучающий", "обучающий - компьютер -
обучаемый", "обучающий - компьютер - группа обучаемых",
"группа обучаемых - компьютер - обучающий", "компьютер -
обучаемый - компьютер";
·
исполнение роли средства
моделирования для получения новых знаний;
·
исполнение роли
"обучения" новых моделей (самообучение модели).
Компьютерное моделирование - основа представления знаний в ЭВМ
(построения различных баз знаний). Компьютерное
моделирование для рождения новой информации использует любую информацию,
которую можно актуализировать с помощью ЭВМ. Прогресс моделирования связан с
разработкой систем компьютерного моделирования, которые поддерживает весь жизненный цикл модели, а прогресс в информационной
технологии - с актуализацией опыта моделирования на компьютере, с созданием
банков моделей, методов и программных систем, позволяющих собирать новые модели
из моделей банка. Автономные подмодели модели обмениваются информацией друг с
другом через единую информационную шину - банк моделей, через базу знаний по компьютерному моделированию. Особенность компьютерных
систем моделирования - их высокая интеграция и интерактивность. Часто эти компьютерные среды функционируют
в режиме реального времени.
Вычислительный эксперимент - разновидность компьютерного моделирования.
Можно говорить сейчас и о специальных пакетах прикладных программ,
текстовых, графических и табличных процессоров, визуальных и когнитивных средах
(особенно, работающих в режиме реального времени), позволяющих осуществлять компьютерное моделирование.
Компьютерное моделирование и вычислительный
эксперимент становятся новым инструментом, методом научного познания, новой
технологией из-за возрастающей необходимости перехода от исследования линейных математических моделей систем
(для которых достаточно хорошо известны или разработаны методы исследования,
теория) к исследованию сложных и нелинейных математических моделей систем (анализ которых гораздо сложнее); грубо, но образно, говоря:
"наши знания об окружающем мире - линейны и детерминированы, а процессы в
окружающем мире - нелинейны и стохастичны".
Информация (абстракция), реализуясь
сообщениями реального мира, овеществляется в разных предметных процессах, а
реализация на компьютере вызывает необходимость использования в компьютерах
специальных формализованных описаний, представлений этих процессов.
Компьютерное моделирование, от постановки задачи до получения
результатов, проходит следующие этапы компьютерного
моделирования.
1) Постановка задачи.
a.
Формулировка задачи.
b.
Определение цели и приоритетов
моделирования.
c.
Сбор информации о системе,
объекте моделирования.
d.
Описание данных (их структуры,
диапазона, источника и т.д.).
2) Предмодельный анализ.
a.
Анализ существующих аналогов и
подсистем.
b.
Анализ технических средств
моделирования (ЭВМ, периферия).
c.
Анализ программного обеспечения
(языки программирования, пакеты прикладных программ,
инструментальные среды).
d.
Анализ математического
обеспечения (модели, методы, алгоритмы).
3)
Анализ задачи (модели).
a.
Разработка структур данных.
b.
Разработка входных и выходных
спецификаций, форм представления данных.
c.
Проектирование структуры и состава
модели (подмоделей).
4)
Исследование модели.
a.
Выбор методов исследования
подмоделей.
b.
Выбор, адаптация или разработка
алгоритмов, их псевдокодов.
c.
Сборка модели в целом из
подмоделей.
d. Идентификация модели, если в этом есть необходимость.
e.
Формулировка используемых
критериев адекватности, устойчивости и чувствительности модели.
5) Программирование
(проектирование программы).
a.
Выбор метода тестирования и
тестов (контрольных примеров).
b.
Кодирование на языке
программирования (написание команд).
c.
Комментирование программы.
6) Тестирование и отладка.
a.
Синтаксическая отладка.
b.
Семантическая отладка (отладка
логической структуры).
c.
Тестовые расчеты, анализ
результатов тестирования.
d. Оптимизация программы.
7) Оценка моделирования.
a. Оценка средств моделирования.
b. Оценка адекватности моделирования.
c.
Оценка чувствительности модели.
d.
Оценка устойчивости модели.
8) Документирование.
a.
Описание задачи, целей.
b.
Описание модели, метода,
алгоритма.
c.
Описание среды реализации.
d.
Описание возможностей и
ограничений.
e.
Описание входных и выходных форматов,
спецификаций.
f.
Описание тестирования.
g.
Создание инструкций для
пользователя.
9) Сопровождение.
a.
Анализ применения, периодичности
использования, количества пользователей, типа использования (диалоговый,
автономный и др.), анализ отказов во время использования модели.
b.
Обслуживание модели, алгоритма,
программы и их эксплуатация.
c.
Расширение возможностей:
включение новых функций или изменение режимов моделирования, в том числе и под
модифицированную среду.
d.
Нахождение, исправление скрытых
ошибок в программе, если таковые найдутся.
10) Использование модели.
Пример. Математическое и компьютерное
моделирование подробно, поэтапно, мы рассмотрим на примере следующей простой
модели производства. Итак, возьмем укрупненные этапы моделирования
производства.
Этап 1. Содержательная
постановка задачи
Современное производство характерно тем, что часть производимой
продукции (в стоимостном выражении) возвращается в виде инвестиций (т.е. части
конечной продукции, используемой для создания основных фондов производства) в
производство. При этом время возврата, ввода в оборот новых фондов может быть
различным для различного рода производства. Необходимо промоделировать эту
ситуацию и выявить динамику изменения величины основных фондов производства
(капитала).
Сложность и многообразие, слабая структурированность и плохая формализуемость основных экономических
механизмов, определяющих работу предприятий, не позволяют преобразовать процедуры принятия решений в экономической системе в
полностью эффективные математические модели и алгоритмы прогнозирования.
Поэтому целесообразно использование простых, но гибких и надежных процедур
принятия решения.
Рассмотрим одну такую простую модель социально-экономического процесса.
Этап
2. Формулировка гипотез, построение, исследование модели
Динамика изменения величины капитала определяется в нашей модели, в
основном, простыми процессами производства и описывается так называемыми
обобщенными коэффициентами амортизации (расхода фондов) и потока инвестиций
(часть конечного продукта, используемого в единицу времени для создания
основных фондов). Эти коэффициенты - относительные величины (оцениваются за
единицу времени). Необходимо разработать и исследовать модель динамики основных
фондов. Считаем при этом допустимость определенных гипотез, определяющих
систему производства.
Пусть x(t) - величина основных фондов (капитала) в момент времени t, где
0<=t<=N. Через промежуток времени 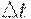 она будет равна она будет равна 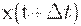 . Абсолютный прирост равен . Абсолютный прирост равен 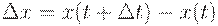 . Относительный
прирост будет равен . Относительный
прирост будет равен ![Описание: \delta x=[x(t+\Delta t)-x(t)]/\Delta t](l7p01.files/image018.gif) . .
Примем следующие гипотезы:
1.
социально-экономические условия
производства достаточно хорошие и способствуют росту производства, а поток
инвестиций задается в виде известной функции y(t) ;
2.
коэффициент амортизации фондов
считается неизменным и равным m, и при достаточно малом значении 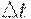 , изменение основных фондов прямо пропорционально текущей величине
капитала, т.е. dx=y(t) - mx(t). , изменение основных фондов прямо пропорционально текущей величине
капитала, т.е. dx=y(t) - mx(t).
Считая  , а также учитывая определение производной, получим из предыдущего
соотношения следующее математическое выражение закона изменения величины
капитала - математическую модель (дифференциальное уравнение) динамики
капитала: , а также учитывая определение производной, получим из предыдущего
соотношения следующее математическое выражение закона изменения величины
капитала - математическую модель (дифференциальное уравнение) динамики
капитала:
x`(t) = y(t) - mx(t), x(0)=х0,
где х(0) - начальное значение капитала в момент времени t=0.
Эта простейшая модель не отражает важного факта: социально-экономические
ресурсы производства таковы, что между выделением инвестиций и их введением и
использованием в выпуске новой продукции проходит время (лаг). Учитывая это,
можно записать модель в виде
x`(t) = y(t-T)-mx(t), x(0)=х0
Этой непрерывной, дифференциальной, динамической
модели можно поставить в соответствие простую дискретную
модель:
хi+1=хi +yj - mхi , x0=с, i=0, 1, 2, :, n, 0<j<n,
где n - предельное значение момента времени при моделировании.
Дискретная модель следует из
непрерывной при 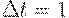 , при замене производной x`(t) на относительное
приращение (из определения производной, это справедливо при малых значениях , при замене производной x`(t) на относительное
приращение (из определения производной, это справедливо при малых значениях 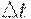 ). ).
Этап
3. Построение алгоритма и программы моделирования
Возьмем для простоты режим моделирования, когда m, c - известны и
постоянны, y - увеличивается на каждый следующий момент времени на 1%, а также
рассмотрим наиболее простой алгоритм моделирования в укрупненных шагах.
1.
Ввод входных данных для
моделирования: с=х(0) - начальный капитал; n - конечное время моделирования; m -
коэффициент амортизации; s - единица измерения времени; y - инвестиции.
2.
Вычисление xi
от i=1 до i=n по рекуррентной формуле, приведенной выше.
3.
Поиск стационарного состояния -
такого момента времени j, 0<=j<=n, начиная с которого все хj, хj +1, :,
хn постоянны или изменяются на малую допустимую
величину 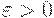 . .
4.
Выдача результатов моделирования
и, по желанию пользователя, графика.
Этап 4. Проведение
вычислительных экспериментов
Эксперимент 1. Поток инвестиций - постоянный и в каждый момент времени
равен 10000. В начальный момент капитал - 1000000 руб. Коэффициент амортизации
- 0,0025. Найти величину основных фондов через 20 суток, если лаг равен 5
суток.
Эксперимент 2. Основные фонды в момент времени t=0 была равны 5000.
Через какое время общая их сумма превысит 120000 руб., если поток инвестиций
постоянный и равен 200, а m=0,02, T=3?
Эксперимент 3. Какую стратегию инвестиций лучше использовать, если
величина инвестиций постоянная, в начальный момент капитал равен 100000,
величина амортизации постоянная?
Этап
5. Модификация (развитие) модели
Модификация 1. Коэффициент амортизации можно взять в форме m=r-sx(t),
где r - коэфициент обновления фондов, s - коэффициент
устаревания фондов, причем 0<=r, s<=1. При этом модель примет вид
x`(t)=y(t-T)-rx(t)+sx2(t), x(0)=х0
Этой непрерывной, дифференциальной, динамической
модели можно поставить в соответствие простую дискретную
модель:
хi+1=хi +yj - rхi+sxi 2 ,
x0=с, i=0, 1, 2, :, n, 0<j<n,
где n - предельное значение момента времени при моделировании. Поставить
цели и исследовать непрерывную и дискретную модели.
Модификация 2. Одна из моделей математической экономики задается уравнением: dz/dt=((1-c)*z(t)+k(t-w)+a)l, где
z(t ) - функция, которая характеризует выпуск
продукции, k - коэффициент капиталовложений, a - независимые расходы
производства, l - скорость реакции выпуска на капиталовложения, c - постоянная
спроса, w - запаздывание (лаг). Поставить цели и
исследовать непрерывную и дискретную модели.
Модификация 3. Для модели динамики фондов с переменным законом потока инвестиций: а)
построить гипотезы, модель и алгоритм для моделирования; б) сформулировать
планы вычислительных экспериментов по этой модели; в)
реализовать алгоритм и планы экспериментов на ЭВМ.
Математическое моделирование только в
последнее время становится на технологическую основу, в связи с этим необходимо
отметить особую роль обычно технологичного имитационного моделирования, которое
позволяет нам проигрывать реальные ситуации, происходящие в системах, на их
моделях. Компьютерное моделирование (получение,
накопление, переработка, хранение, использование, актуализация знаний с помощью
ЭВМ), в отличие от математического, используется сравнительно недавно, хотя эти
технологии моделирования тесно связаны. Компьютерное
моделирование, как правило, применяется тогда, когда не удается построить
математической аналитической модели или же такая модель трудоемка для
исследования.
Пример.
Компьютерной (физической) моделью может служить простая модель броуновского
движения, получаемая генерацией компьютером нового случайного положения точки
на экране и траектории ее движения; при этом отметим, что сам "датчик
случайных чисел компьютера (или языка)" - это компьютерная
модель, соответствующая математической модели распределения случайной величины
(обычно нормального распределения) или так называемой
функции распределения. Это распределение - псевдослучайное, получаемое по
вполне детерминированному алгоритму.
|