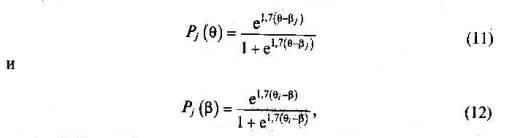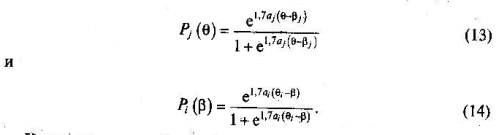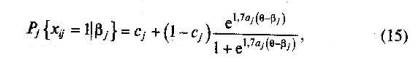Лекция 13. Современная теория конструирования тестов.

 

1.      Основные положения современной теории

2.      Математические модели современной теории тестов.

3.      Оценивание параметров подготовленности учащихся и трудности заданий теста в IRT.

4.      Информационные функции тестовых заданий и теста

5.      Современные программные средства для разработки педагогических тестов.

 

1. Основные положения современной теории

 

Item Response Theory (IRT) и область ее применения. В 80-х гг. XX в в педагогических измерениях получили широкое развитие методы современной теории тестов Item Response Theory, сокра­щенно IRT [60; 65; 75; 83]. Прямой перевод на русский язык исторически сложившегося названия этой теории ничего не го­ворит о ее сути, поэтому в русскоязычной литературе широко используется название «теория IRT». В целом IRT предназначена для оценивания латентных параметров испытуемых и заданий тестов на основе математико -статистических моделей измерения и является частью более общей теории латентно-структурного анализа (LSA), хотя каждое из этих направлений имеет свои ха­рактерные особенности и свою сферу применения. В частности область использования LSA - социально-психологические ис­следования, в то время как IRT применяется в основном для конструирования и интерпретации результатов выполнения пе­дагогических тестов.                                                            

IRT намного эффективнее традиционной теории тестов, по­скольку обеспечивает более высокие точность, уровень измере­ний и качество тестов. Это осуществляется благодаря математико-статистическому аппарату теории, требующему привлечения дорогостоящих программных продуктов, тщательной стратифи­кации выборок испытуемых при разработке тестов и значитель­ным трудозатратам на согласование данных измерения с требо­ваниями математических моделей измерения. Эти трудности раз­работчикам необходимо учитывать при выборе основополагаю­щей теории конструирования тестов.

Латентные параметры и их связь с наблюдаемыми результатами тестирования. Построение теории IRT основано на предположе­нии о существовании функциональной связи между латентными параметрами испытуемых и наблюдаемыми результатами выпол­нения теста. Первопричиной являются латентные параметры ис­пытуемых, взаимодействие которых с заданиями в процессе тес­тирования порождает наблюдаемые результаты выполнения теста. На практике всегда ставится обратная задача: по ответам испытуемых на задания теста оценки значения латентного параметра θ_i, (i = 1, 2, ..., N), определяющие уровень подготовки N испытуемых, и латентного параметра β_j (j = 1, 2, ,.., n), равные оценкам  трудности n заданий теста.                

Для решения этой задачи датский математик Г. Раш предло­жил математическую модель связи между латентными параметра­ми и наблюдаемыми результатами тестирования, содержащую со­отношение между латентными параметрами θ и β в виде разности θ - β при условии, что параметры θ и β оцениваются в одной и той же шкале. В качестве такой единой шкалы Г. Раш ввел интер­вальную шкалу логитов.

Если рассматривать значение параметра θ_i- как положение i-го испытуемого на шкале логитов, а значение β_j — как положение j-го задания на той же шкале, то разность параметров получает инте­ресную геометрическую интерпретацию. Абсолютная величина раз­ности |θ_i - β_j| — это расстояние, на котором находится испытуе­мый с уровнем подготовки θ_i от задания с трудностью βj. Если эта разность велика по модулю и отрицательна, то задание бесполезно для измерения уровня подготовленности i-го ученика, поскольку он наверняка не сможет выполнить такое трудное задание верно. Большие положительные значения этой, разности тоже не пред­ставляют интереса ни для процесса контроля, ни для обучения i-го испытуемого, поскольку они говорят о том, что задания такой: труд­ности давно освоены учащимся и он справится с ними успешно при выполнении теста. С точки зрения подхода, предлагаемого в IRT, такие задания неэффективны для оценивания данного значе­ния θ. Наименьшую ошибку измерения обеспечивают задания, труд­ность которых приблизительно равна уровню подготовленности испытуемого, т.е. задания, подобранные по критерию θ = β.

 

2. Математические модели современной теории тестов

 

Условная вероятность правильного выполнения обучаемыми за­даний теста как функция одной переменной. В качестве математиче­ской модели взаимосвязи между значениями латентных перемен­ных θ, β и наблюдаемыми результатами выполнения теста в IRT выбрана условная вероятность правильного выполнения обучаемыми заданий теста. В частности можно рассматривать условную вероят­ность Pj правильного выполнения /-м испытуемым с уровнем под­готовки θ_i, различных по трудности заданий теста, считая θi, пара­метром i-го ученика β — независимой переменной.

Аналогично вводится Рj для обозначения вероятности правильного выполнения i-го задания трудностью βj; различными испыту­емыми группы. Здесь θ — независимая переменная, а βj; — пара­метр, определяющий трудность j-го задания теста:

 

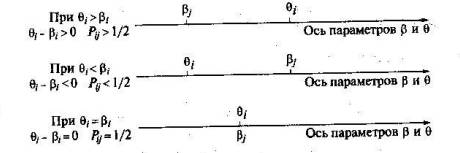
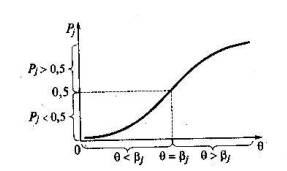
f и  φ — символы функциональной зависимости; N — число испы­туемых; n — количество заданий в тесте.

Если подставить в функцию Pj(θ) значение переменной θ=θ_i, или в функцию P_i(β) значение  β = β_j ;, то получится выражение для вероятности Р_ij значения которой можно охарактеризовать сле­дующим образом:

Р_ij ->1, когда θ_i- βj, намного больше 0;

Р_ij -> 0, когда θ_i - βj - намного меньше нуля;

Р_ij =1/2 при θ_i – βj.

Геометрическая интерпретация связи между разностью латент­ных параметров и вероятностью правильного ответа на задания те­ста. Связь между значениями разности θi - βj и вероятностью пра­вильного ответа i-го испытуемого на j-е задание теста показана на рис.26.

В теории IRT график функции Рj получил название характери­стической кривой j-го задания (ICC), а график функции Pi — индивидуальной кривой i-го испытуемого (РСС).

При выборе вида функций Pj и Рi, учитываются обстоятельства как эмпирического, так и математического характера. В предполо­жении нормального распределения значений латентных перемен­ных θ и β предлагаются две такие функции. Одна из них, обычно обозначаемая символом ψ(х), относится к семейству логистичес­ких кривых, другая — Ф(х) — является интегральной функцией нормированного нормального распределения. Поскольку для одних и тех же значений х ординаты точек графиков функций Ф(х) и ψ (1,7х) отличаются друг от друга незначительно, то в том, что их две, нет ни ошибки, ни противоречия. Наиболее убедительный аргумент в пользу логистической функции связан не с качеством измерений, а с относительной простотой ее аналитического зада­ния, облегчающей оценивание параметров θ и β Поэтому в практи­ческих приложениях предпочтение обычно отдают функции ψ (1,7х)

Рис. 26. Соотношение между значениями разности  θ_i – βj и вероятностью

правильного ответа

 

Классы логистических функций. Число параметров, входящих в аналитическое задание функций,  является основанием для под­разделения семейств логических функций на классы. Среди логи­стических функций различают:

1)      однопараметрическую модель Г. Раша —

 

гдеθ и β  — независимые переменные для первой и второй функ­ций соответственно;

2)      двухпараметрическую модель А. Бирнбаума —

Кроме прежних обозначений в формулах (13) и (14) появля ются параметры а_i и a_j,. Параметр a_j - был введен А. Бирнбаумом для характеристики дифференцирующей способности задания при измерении различных значений θ. Параметр a_i- указывает на меру структурированности знаний i-го ученика;

3)      трехпараметрическую модель А. Бирнбаума

где Cj является третьим параметром модели, характеризующим вероятность правильного ответа на  j-е задание в том случае, если этот ответ угадан, а не основан на знаниях

В каждой из представленных моделей параметры  θ и β выража­ются как шкалированные показатели единой для всех моделей шкалы логатов. Введение единой шкалы для элементов двух различных множеств позволяет подобрать оптимальные значения, % дающие возможность измерить искомое θ с минимальной ошиб­кой измерения. Перевод значений вире общую шкалу логитов с помощью специальных преобразований был предложен Б.Д.Рай­том и М. Г.Стоуном [83]. Подробно он рассмотрен в книге М.Б.Челышковой «Теория и практика конструирования педагогических тестов» [60].

Однопараметрическая модель Г.Раша. Аналитическое задание однопараметрической модели Г.Раша представлено формулами (16) и (12). В первом случае вероятность правильного выполнения j-го задания теста является возрастающей функцией от перемен­ной θ. Это свойство функции согласуется с практическим опытом педагога, Естественно ожидать, что чем больше уровень подготов­ки испытуемого, тем больше вероятность правильного выполне­ния им j-го задания теста..

На рис. 27 изображена характеристическая кривая j-го задания теста, показывающая взаимосвязь между значениями независи­мой переменной θ и величиной Pj . Точке перегиба характеристи­ческой кривой соответствует значение θ = β_j, а P_j- в этой точке равно 0,5.         

 

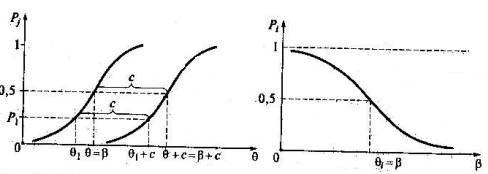
Рис.27. Характеристическая кривая j-го задания теста

                                .

Свойство инвариантности оценок параметра испытуемых от труд­ности заданий теста. Модель Раша обладает интересным свойством, позволяющим на репрезентативной выборке испытуемых реали­зовать идею инвариантности оценок параметров θ и β, которая не характерна для двух и трех параметрических моделей. Не останав­ливаясь на математическом доказательстве, можно привести не­сложную геометрическую интерпретацию свойства инвариантно­сти (см. рис. 28).

Пусть испытуемый с уровнем подготовки θ₁ ответит на задание j с вероятностью P_1. Увеличение трудности j-го задания теста на константу с (с > 0) вызовет смещение характеристической кри ой вправо. C прежней вероятностью на это более трудное зада­ние будет отвечать испытуемый с уровнем подготовки θ₁ + с. Так как θ – β_j = (θ + с) - (β_j + с), то значение вероятности правильного ответа Р₁ не изменится, что дает основание для вывода об относительной инвариантности уровня подготовки испытуемых от труд­ности заданий теста.

Рис. 28. Иллюстрация инвариантности

         оценок уровня подготовки испытуемых от

трудности заданий теста

                                                                       Рис. 29 Индивидуальная кривая i-го испытуемого

 

Вероятность правильного выполнения i-м испытуемым различ­ных по трудности заданий Pi является убывающей функцией пе­ременной β. Это означает, что с ростом трудности заданий значения вероятности P_i (β) будут уменьшаться. График функции Рi(β) представлен на рис. 29.                  

В точке перегиба кривой, соответствующей значению независи­мой переменной θ_i = β, функция P_i (β) принимает значение P_i = 0,5. В процессе обучения по мере накопления знаний индивидуальная кривая испытуемого смещается вправо.

Поскольку вдоль кривой откладываются доли правильных от­ветов на задания, которые не зависят от характера распределения группы тестируемых учеников, форма характеристической кри­вой задания и ее положение при построении кривой на выборках в цервой слабой и во второй сильной группах получатся одними и теми же (рис. 30). Конечно, практика свидетельствует о том, что эффект инвариантности наблюдается далеко не всегда, а только в тех случаях, когда реальная статистика — доли правильных отве­тов учащихся на задания — лежит достаточно близко к теорети­ческой кривой. Причем чем ближе подходят точки распределения долей к кривой. — графику функции P_j тем ярче проявляется инвариантность.

 

Рис. 30. Иллюстрация инвариантности формы характеристической кри­вой задания от уровня подготовленности тестируемой выборки

 

3. Оценивание параметров подготовленности учащихся и трудности заданий теста в ИНГ

Начальные оценки параметра испытуемых и параметра трудно­сти заданий теста. Начальные оценки параметра подготовки уча­щихся в логитах находят по формуле

 

 где θ_i⁰ — уровень подготовленности i-го ученика; p_i и q_i — доли правильных и неправильных ответов соответственно, подсчитан­ные по матрице наблюдаемых результатов выполнения теста; In — символ натурального логарифма.

Начальные оценки параметра трудности заданий β получают по формуле

где p₁  и q₁  -  доли правильных и неправильных ответов на j-е задание теста, соответственно; In — символ натурального логарифма. Как следует из формул для подсчета, оценки параметров вир могут меняться в интервале (-∞, +∞), но практически при θ_i,- -β < -5 значения Р_ij близки к нулю. Аналогичная пограничная ситуация наблюдается, когда θ_i — β_j> 5. В этом случае значения вероятности P_ij  будут почти равны 1. Поэтому значения разностей параметров, выходящие за указанные пределы, не рассматриваются в практи­ке педагогических измерений.

Свести оценки логатов подготовленности испытуемых и логитов трудности заданий в единую шкалу позволяют специальные преобразования, выполняемые после завершения подсчетов на­чальных оценок θ и β. Вслед за преобразованиями оценки каждого из параметров выражаются в интервальной шкале с одним значе­нием среднего и стандартного отклонения.

Метод наибольшего правдоподобия. Хотя теория IRT обеспечи­вает инвариантность оценок параметров θ и β, на практике в силу действия различных случайных факторов свойство инвариантно­сти не выполняется в полной мере. Если объем выборки испытуе­мых достаточно велик, то можно, ставить вопрос вычислении устойчивых значений параметров θ и β, которые будут наиболее эффективными оценками и могут быть приняты в качестве объек­тивных значений этих параметров.

Существуют различные методы вычисления эффективных оце­нок параметров распределения. Одним из них является метод наи­большего правдоподобия, предложенный Р. Фишером [63] и реа­лизуемый итерационными процедурами с помощью специальных программных продуктов на ПК. Применение Метода наибольшего правдоподобия требует введения предположения о локальной не­зависимости заданий теста, которое означает, что при данном зна­чении 6 вероятность правильного ответа на конкретное задание те­ста не зависит от результатов выполнения остальных его заданий. Для вычисления эффективных оценок параметров составляет­ся вероятностная модель выполнения заданий теста группой ис­пытуемых, которая называется функцией правдоподобия. Значе­ния параметра θ, при которых функция правдоподобия достигает максимума, принимается в качестве объективных оценок пара­метра подготовленности испытуемых. Таким же образом вычисля­ются оценки наибольшего правдоподобия для параметра трудно­сти заданий теста. Согласно теории оценки наибольшего правдо­подобия являются наиболее эффективными и могут быть приня­ть за истинные значения латентных переменных θ и β.

 

4. Информационные функции тестовых заданий и теста

 

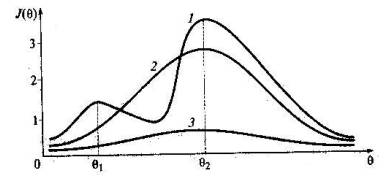
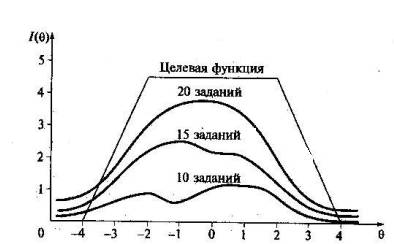
Понятие «информационная функция». В отличие от классичес­кой теории тестов, не позволяющей прогнозировать надежность измерений, в IRT можно априорно получать дифференцирован­ные оценки точности, обеспечиваемой j-м заданием теста в раз­личных точках оси θ. Эти оценки основаны на подсчете значений информационной функции, введенной А. Бирнбаумом. По одно­му из определений, предложенных этим исследователем, количе­ство информации, обеспеченное j-м заданием теста в данной точ­ке θ — это величина, обратно пропорциональная стандартной ошибке измерения данного значения θ с помощью задания j.

Соответствие количества информации, получаемой при оце­нивании параметра θ с помощью задания j, и различных точек оси в отражается с помощью специальной функции, получившей на­звание информационной. Значения этой функции являются свое­образной характеристикой эффективности j-го задания в каждой  точке оси латентной переменной θ. Чем больше количество информации, тем лучше, образно говоря, работает задание на рас­сматриваемом интервале оси θ .

Информационная кривая теста. Благодаря свойству аддитивно­сти информация, полученная при измерении данного θ с помо­щью всего теста, складывается из отдельных значений ординат информационных функций, построенных для каждого задания теста. На рис. 31 приведены графики трех информационных функ­ций, одна из которых (кривая 1) имеет две точки максимума θ₁ и θ₂, что недопустимо в правильно сконструированном тесте.

Кривая 2 на том же рисунке принадлежит менее информатив­ному тесту, проигрывающему в точности измерений тесту, пред­ставленному кривой /, при оценке подготовленности учащихся в окрестности точки θ₂. Однако у кривой 2 есть явное преимущество по сравнению с кривой 1, поскольку она имеет один четко выра­женный максимум, что позволяет отдать ей предпочтение при срав­нительном анализе качества первого и второго тестов. Пологая кривая 3 отображает неудачный тест, который является малоин­формативным на всем протяжении оси θ.

Моделирование теста. В тех случаях, когда есть банк калибро­ванных заданий, тест можно моделировать с помощью информа­ционных функций, построенных на том участке оси θ, где по предварительным данным (экспресс-диагностика или опыт пред­варительного контроля учащихся) будут в основном расположе­ны оценки подготовленности испытуемых. За счет специального подбора заданий на основе графика целевой информационной функ­ции теста появляется возможность оптимизировать подбор труд­ности теста и минимизировать стандартную ошибку измерения на нужном интервале оси θ.

В целом процесс моделирования теста, представленный, на рис. 32, включает следующие этапы:

- построение целевой информационной кривой теста, обеспе­чивающей заданную стандартную ошибку измерения в нужном интервале оси θ;

-выбор заданий из банка с информационными кривыми, удов­летворительно заполняющими пространство под целевой инфор­мационной кривой теста;

- сложение ординат информационных кривых тестовых зада­ний в каждой точке оси латентной переменной в и пошаговое построение информационной кривой получаемого теста;

- продолжение процесса выбора заданий до тех пор, пока пло­щадь под целевой кривой не будет заполнена с заданной степе­нью точности;

- проверка абсолютного значения разности между максималь­ной суммой ординат информационных кривых заданий и плани­руемым максимумом на целевой кривой в разных точках оси θ.

 

Рис. 31. Информационные кривые трех тестов

 

 

Рис. 32. Информационные кривые моделируемого теста

 

Имея информационные функции, можно сравнить эффективность различных моделируемых тестов с исходным эталонным без предва­рительного сбора эмпирических данных. Для этого используют функ­цию сравнительной эффективности, представляющую собой отно­шение двух информационных функций: эталонной функции и функ­ции моделируемого теста. Вычисление значений функции сравнительной эффективности позволяет оценить эффект при удалении из теста заданий определенной трудности, при замене заданий средней трудности на легкие или более трудные задания, а также решить ряд других вопросов, возникающих у создателя тестов.

 

5. Современные программные средства для разработки педагогических тестов

Программные средства для конструирования тестов: общая ха­рактеристика. Интенсивное развитие программных средств, реа­лизующих алгоритмы IRT, и классической теории для конструи­рования новых тестов началось в конце 80-х гг. XX в. и продолжается в настоящее время. Программные продукты для конструиро­вания тестов нередко путают с инструментальными средствами для компьютерного тестирования, хотя они имеют разное назна­чение. Первые создаются для анализа эмпирических данных тес­тирования в целях коррекции характеристик тестов, обеспечения высокого качества педагогических измерений, калибровки зада­ний при наполнении банков, шкалирования и выравнивания для построения стандартных шкал по данным педагогических изме­рений. Вторые выполняют исключительно функцию поддержки при проведении компьютерного тестирования и обеспечивают фор­мирование вариантов тестов, их предъявление, накопление баз данных по результатам тестирования и оценку результатов уча­щихся для выдачи им тестового балла. При правильном Положе­нии вещей оба блока программных продуктов должны работать совместно, поскольку информацию о результатах тестирования, накапливаемую в инструментальной оболочке, необходимо пере­давать дальше для совершенствования характеристик теста.

Часть разрабатываемых в мире программ для конструирования тестов носит закрытый характер и используется исключительно для собственных нужд, как, например, в ETS. Другая часть попа­дает на рынок благодаря каталогам и Интернету. Материалы, раз­мещенные в Интернете крупнейшими разработчиками и распро­странителями программного обеспечения для конструирования те­стов, включают описания технологий, перечень возможностей программ, демонстрационные версии и т.д.

Виды программных продуктов для конструирования тестов. К числу наиболее интересных программ, созданных мировым лидером в компьютерном тестировании Assessment Systems Corporation (ASC), можно отнести RASCH, RASCAL, Quest, ConQuest, а также XCALIBRE, ASCAL, LOGIMO, MSP, PARELLA и многие другие [91]. Некоторые из разработок корпорации ASC, например, MieroCAT, CAT, позволяют реализовывать адаптивные варьиру­ющие алгоритмы с переменным шагом и осуществлять процессы генерации адаптивных тестов. В настоящий момент наибольший интерес для разработчика и пользователя тестов представляют следующие программы:

- AGREE, предназначенная для расчета согласованности оце­нок в номинальных шкалах данных в случае, когда два и более экспертов классифицируют объекты по некоторым категориям но­минальной шкалы;

-  ASC Item and Test Analysis Package — пакет программ ASC для анализа качества тестов и шкалирования результатов их вы­полнения. Программы пакета позволяют осуществить простейший анализ качества заданий по классической теории тестов, в том числе и углубленный дистракторный анализ (ITEMAN), получить оценки параметров подготовленности испытуемых и трудности заданий по однопараметрической модели теории IRT (RASCAL), провести калибровку заданий (XCALIBRE), получить данные входного тестирования для эвалюации (Test PreEvaluation), оценить валидность теста (Test Validation), провести автоматизированную оценку результатов выполнения заданий и получить шкалирован­ные баллы учащихся (Test Scoring) и т.д.;

-  BILOG^NEW, позволяющая получить, оценки параметров тес­товых заданий на Основе.теории IRT использованием одно-, двух-  и трехпараметрических логистических моделей и перейти к наи­более эффективным оценкам параметров по методу максималь­ного подобия с помощью реализации итерационных процессов (только для дихотомических оценок по отдельным заданиям теста);

- ConQuest — универсальная программа, включающая различ­ные модели IRT, в том числе для полигамических оценок по за­даниям в случае одномерных и многомерных измерений;

- FastTEST^NEW — 32-bit Windows система для поддержки банка калиброванных тестовых заданий и моделирования различных тес­тов, поддерживающая режимы бланкового и компьютерного предъявления параллельных вариантов тестов и оценки их качества с помощью моделей IRT для дихотомических данных по заданиям;

-  FastTEST Professional^EW — система для адаптивного тести­рования с использованием теории 1RT. Считается наиболее про­двинутой системой компьютерного адаптивного тестирования в мире;

-  1TEMAN — статистика заданий и тестов с использованием классической теории тестов и данных опросов (по типу Лайкёрта). Наиболее популярный в мире программный продукт для анализа тестов;

- MicroCAT — полная оболочка для создания тестов и прове­дения тестирования (как компьютерного, так и бланкового) и последующего анализа результатов;

- PARSCALE^NEW — предназначена для шкалирования резуль­татов учащихся на основе теории IRT, позволяет проводить ана­лиз качества заданий и построение рейтинговых шкал;

-  XCALIBRE, позволяющая получить оценки наибольшего правдоподобия на основе алгоритмов ЕМ для небольших выборок испытуемых или коротких тестов для двух- и трехпараметриче­ских моделей IRT.