|
Лекция 16. Шкалирование результатов тестирования.
1. Задачи шкалирования. 2. Построение шкал. 3. Виды шкал в образовании. 4. Шкалирование результатов тестирования на основе теории IRT. 5. Шкалирование в критериально-ориентированном тестировании. 6. Рейтинговые шкалы.
1. Задачи шкалирования.
Для чего и когда следует использовать процедуру шкалирования. Для обоснованного сопоставления результатов учащихся между собой тестовые баллы в соответствии с рядом критериев и норм (число правильно выпаженных заданий при дихотомической оценке результатов выполнения каждого задания, сумма оценок по отдельным заданиям при политомической, или взвешенной, оценке) переводятся в производные показатели при помощи процедуры, которая получила название шкалирования. Таким образом, процесс шкалирования состоит в преобразовании сырых баллов в производные показатели, обеспечивающие адекватную интерпретацию и сравнение результатов выполнения педагогических тестов [1; 21; 22; 60]. Современная трактовка процесса шкалирования. Процесс шкалирования включает в себя различные процедуры. В простейшем случае под шкалированием понимается отображение сырых баллов на готовую шкалу, производимое по "определенным правилам. Перевод сырых баллов в производные показатели и их размещение на готовой шкале не могут повысить надежность и валидность данных по тесту. В современной литературе по теории педагогических измерений встречается расширенное понимание процедуры шкалирования, в которую включают конструирование шкалы по определенным правилам и последующее преобразование исходных эмпирических данных для помещения их на данную шкалу. Таким образом, согласно расширенной трактовке, шкалирование включает ряд последовательных этапов, охватывающих все компоненты педагогических измерений, и имеет связь с качеством результатов.
2. Построения шкал для педагогических измерений
Этапы Шкалирования. При трактовке процесса шкалирования в расширенном варианте можно выделить четыре основных этапа построения измерительных шкал в образовании для ситуации бланкового тестирования и обобщенного случая измерений: Этап 1 — определение цели измерения, выбор конструкта, размерности и содержательной области, адекватно описывающей конструкт. Этап 2— разработка заданий и экспертное обоснование их качества, экспертное оценивание адекватности содержания заданий конструкту, определение первоначальной длины теста. Этап 3 — апробация, эмпирический анализ качества теста, чистка и коррекция измерителя для повышения надежности и валидности шкалы, проверка размерности пространства измерений или доказательство одномерности теста, Этап 4 — подтверждение качества шкалы и анализ возможности ее использования для представления результатов учащихся по тесту. Последний этап начинается с построения устойчивой шкалы, выбранной в соответствии с целями измерения и подходом к созданию теста. При последующем использовании теста сырые баллы учеников отображаются на готовой шкале, Особую важность на данном этапе имеет процедура выравнивания результатов педагогических измерений, полученных учащимися по разным вариантам теста. Необходимость выравнивания может быть не совсем понятна педагогу-практику, поскольку е школе принято выдавать существенно различающиеся но трудности варианты контрольных работ, а затем присваивать одинаковые оценочные эквиваленты разным, зачастую несопоставимым, результатам учащихся. В практике педагогических измерений утвердилась другая норма сравнения и интерпретации результатов испытуемых, основанная на выравнивании, которое представляет собой статистический метод преобразования оценок испытуемых по различным вариантам для обеспечения их сопоставимости.
3. Виды шкал в образовании
Общие цели шкалирования. Процесс шкалирования реализует разные цели в зависимости от подхода, выбранного к разработке теста. При нормативно-ориентированном подходе шкалированные показатели позволяют уточнить место, занимаемое результатом испытуемого относительно норм, или сравнить результаты испытуемых, установив место результата каждого учащегося по отношению к результатам остальных учащихся, выполнявших этот тест При критериально-ориентированном подходе шкалированный балл показывает процент освоенного содержания и место результата учащегося в сравнении с критериальным баллом. Перечисленным целям отвечают разные шкалы, которые можно построить по результатам выполнения теста. Шкала перцентильных рангов. Перцентильный (процентильный) ранг для каждого балла определяется процентом испытуемых, которые выполнили столько же или меньше заданий теста. Например, если 30 % учащихся выполнили верно по 20 заданий теста и получили за каждое из них по одному баллу, то сырой балл «20» соответствует 30-му перцентилю. Таким образом, перцентиль показывает относительное положение испытуемого в выборке учащихся, которая выполняла тест. Чем ниже перцентильный ранг результата испытуемого, тем хуже его результаты по сравнению с другими тестируемыми группы. Перцентили выше 50-го представляют результаты выше среднего по выборке, а перцентили ниже 50-го — ниже среднего, если в качестве средней нормы выступает медиана, которой соответствует 50-й перцентиль. Для 25-го и 75-го перцентилей существуют специальные названия: 1-й и 3-й квартили соответственно. Они отсекают нижнюю и верхнюю четверть распределения тестовых баллов, поэтому их выделение удобно для сравнения результатов данного тестировании с распределениями результатов по другим тестам. .. Бели шкала перцентилей построена на выборке стандартизации, то, используя ее, легко определить ранг каждого учащегося, выполнявшего в другое время тот же тест. Для этого достаточно подсчитать его сырой балл и по готовой таблице соответствия найти соответствующий перцентиль. Первичный балл, который ниже любого результата в выборке стандартизации, будет иметь нулевой перцентильный ранг. Результат, превышающий любой другой в выборке, получит перцентильный ранг 100. Конечно, оба эти результата не говорят о нулевом или абсолютном результате выполнения теста. Перцентили не следует путать с обычными про-< центными показателями, которые при дихотомическом оценивании результатов выполнения отдельных заданий представляют собой выраженную в процентах долю правильно выполненных заданий теста. В отличие от обычных процентов перцентиль является производным показателем, который оценивается в единицах процента испытуемых. Перцентили имеют несомненные достоинства — они удобны в подсчете и просты в интерпретации. Помимо достоинств перцентильные ранги имеют два существенных недостатка. Во-первых, они являются значениями порядковой шкалы, так как показывают относительное положение каждого индивида в нормативной выборке, а не определяют величину истинного различия между результатами отдельных испытуемых группы. Во-вторых, перцентили не только не отражают, но даже искажают реальные различия в результатах выполнения теста. Это связано с особенностями распределения перцентилей, имеющего прямоугольный характер. В этой связи небольшие отклонения от среднего в центре распределения наблюдаемых баллов будут значительно увеличены перцентилями, в то время как относительно большие отклонения на краях кривой нормального распределения будут сжаты. Стандартные показатели. Z-шкала. При выборе метода шкалирования часто обращаются к стандартным показателям, указывающим отличие индивидуального результата испытуемого от среднего балла повыборке в единицах стандартного отклонения. Эти показатели используются для установления места первичного балла каждого испытуемого в сравнении с результатами других на основе подсчета нормированных отклонений и называются z-оценками. Результат отображения z-оценок на числовую ось образует Z-шкалу. Для перевода в Z-шкалу сырой балл i-го испытуемого преобразуется по формуле
где Xi — сырой балл i-го испытуемого; X — среднее значение индивидуальных баллов N испытуемых группы; Sx — стандартное отклонение. Поскольку среднее значение X вычитается из каждого исходного значения Xi, то новое среднее в Z-шкале — z — будет равно нулю, а стандартное отклонение благодаря нормированию будет равно единице. Если величина разности Xi-X, стоящей в числителе дроби, больше 0, то результат i-го испытуемого выше среднего по тесту. В противном случае индивидуальный балл i-го испытуемого ниже среднего. В силу линейного характера преобразований при получении г-оценок все свойства исходного распределения сырых баллов переносятся на множество шкалированных баллов. Использовать Z-шкалу можно для любого распределения индивидуальных баллов. Особенно удобны z-оценки в случае близости распределения первичных баллов к требованиям нормального закона, поскольку можно заранее предсказать процент результатов, лежащих в пределах одного и двух стандартных отклонений под кривой нормального распределения. Несомненным достоинством Z-шкалы является общая средняя арифметическая и общая мера вариации данных, позволяющие достичь сравнимости результатов по разным тестам. Однако помимо явных достоинств есть и недостатки. Отрицательные и дробные оценки, которые нередко получаются при вычитаний среднего и деления на стандартное отклонение, малопригодны для сообщения результатов тестирования испытуемых группы. Поэтому применяются специальные, методы линейного преобразования z-оценок для перевода их на множество целых положительных чисел. Шкалы стандартных оценок, полученных на основе линейных преобразований Z - шкалы. Для перевода - оценок в область положительных целых чисел выбираются новые значения среднего арифметического (М) и стандартного отклонения (σ). Они сохраняют все различия между баллами испытуемых, выявленные в Z-шкале, но позволяют избавиться от отрицательных и дробных значений z благодаря умножению каждой z -оценки на одно и то же число, а также прибавлению общей константы и последующему округлению. Для преобразования z-оценок используется формула z1=M + σz (19)
где М — новое среднее арифметическое; σ - новое стандартное отклонение.
В качестве значений M и σ в формуле (19) можно использовать любые удобные числа. Например, для шкалы IQ эти значения равны 100 и 15. Поэтому zIQ =100+15z. Другое линейное преобразование c M = 50+10z переводит значения z в стобалльную T-шкалу по формуле Т = 50 + 10z. Эта шкала позволяет избавиться от дробных и отрицательных значений только в том случае, если значения z лежат в интервале от -5 до +5 и имеют один знак после запятой. В противном случае, если показатели подсчитаны с точностью до сотых, необходимо последующее округление T-показателей, что может привести к снижению дифференцирующего эффекта теста. Для шкалы СЕЕВ по тестам SAT (Scolastic Aptitude Test), разработанным Советом по приемным экзаменам в колледжи, z-оценки пересчитываютcя со средним М = 500 и σ = 100 по формуле zCEEB= 500 + 100z. Значению z = -1 будет соответствовать значение zCEEB = 500 + 100 (-1) = 400. A при z = +1 т- zCEEB = 600. Таким образом, в шкале СЕЕВ все дробные z-оценки превращаются в целые и попадают в интервал (0; 1000) в тех случаях, когда Z лежит в интервале (-5; +5). Так же в тысячебалльную шкалу переводятся оценки результатов выполнения таких известных в мире тестов, как GRE (Graduate Record Examination) и. др. Сопоставимость и выравнивание. Поскольку обеспечение сопоставимости результатов педагогических измерений является одной из главных причин перехода от сырых баллов к производным показателям в процессе шкалирования, то возникает вопрос о возможности сравнения z-оценок, полученных на основе различных вариантов тестя. Ответ на этот вопрос на теоретическом уровне носит, несомненно, положительный характер в тех случаях, когда сравниваются z-оценки по параллельным вариантам одного и того же теста. Однако на практике из-за неизбежных отклонений от требований параллельности и существования ошибок измерения для повышения сопоставимости оценок испытуемых обычно используют процедуру выравнивания.
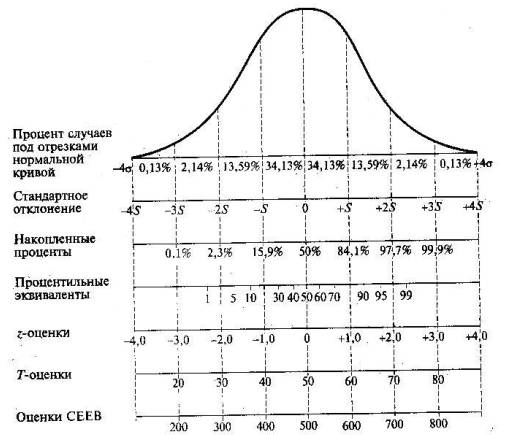
Рис. 33. Сопоставление шкал
В отдельных случаях возникает необходимость сравнения относительного положения испытуемых, полученного в различных шкалах и по различным тестам. Если результаты тестирования имеют нормальное распределение, а выстроенные шкалы основаны на идентичных выборках испытуемых, такое сравнение можно провести с помощью рис. 33. Чтобы добиться сопоставимости результатов тестирования в ситуации отличия распределений баллов от нормального закона, необходимо преобразование, изменяющее вид кривой распределения с целью приближения ее к виду нормальной кривой. Нормализация данных тестирования. Для нормализации данных тестирования используется нелинейное преобразование, позволяющее придать эмпирическому распределению желаемую форму нормальной кривой. С этой целью вводятся нормализованные стандартные показатели, соответствующие распределению, преобразованному так, что оно аппроксимируется формой нормальной кривой. Их значения могут быть найдены с помощью таблиц, в которых приводится процент случаев различных отклонений в единицах от среднего значения для нормальной кривой. Преобразование сырых баллов к нормальному распределению осуществляется способом, получившим название пробшп-преобразования [1; 18]. В рамках процедуры преобразования баллов сначала для каждого сырого показателя определяется кумулированная частота, которая представляет собой сумму всех частот, лежащих ниже данного сырого показателя. Затем к ней добавляется половина количества испытуемых, имеющих этот сырой балл. По этим данным вычисляется кумулированная доля путем деления полученной суммы на общее число испытуемых выборки. Затем по статистическим таблицам, содержащим значения площади под кривой нормального распределения, находят значения нормализованных стандартных Показателей для каждой кумулированной доли |63]. Нормализованный стандартный показатель, как и линейно преобразованный стандартный показатель, имеет среднее значение «О», а стандартное отклонение — «1». Результат учащегося в «-1» балл можно интерпретировать как превосходящий приблизительно 16% результатов группы, а в «+1» балл — как превосходящий 84 % всех результатов. Шкала станайнов, стенов и другие шкалы. Нормализованным стандартным показателям, так же как и линейно преобразованным, стараются придать удобную форму, пригодную для сообщения испытуемым. Для этого используют шкалы стандартных десяти или девяти единиц. Разбиение нормального распределения на девять интервалов приводит к шкале станайнов, имеющей девять стандартных единиц. Название «станайн» связано с тем, что оценки в этой шкале принимают значения от «1» до «9». При оценке результатов испытуемых по тесту 4 % самых худших результатов присваивается станайн 1, а самых лучших — станайн 9. Следующим за худшими и лучшими 7 % результатов присваивают ста-найны 2 и 8 соответственно. Далее 12 % результатов — станайны 3 и 7. Следующим 17% присваивают станайны 4 и б и, наконец, 20% средних результатов — станайн 5 (табл. 16). . Помимо описанной шкалы станайнов существуют еще две шкалы, имеющие некоторое, преимущество перед девятибалльной в смысле различающей способности. Одна из них — шкала стандартных десяти единиц, называемая также шкалой Кэтгелла, или шкалой стенов (sten). Как следует из названия, весь массив результатов делится на десять частей с интервалом 0,5 стандартного отклонения. В шкале стенов среднее арифметическое принимается равным 5,5, а расстояние между двумя соседними стандартными единицами равно 0,5 Sx.
Таблица 16 Таблица соответствия процентов и станайнов
Какие шкалы использовать в педагогических измерениях. Многие из шкал, приведенных выше, используются исключительно психологами, другие нашли свое применение в образовании. В практике деятельности зарубежных тестовых служб в образований чаще всего обращаются к стобалльной или тысячебалльной шкале, полученным на основе преобразования z-оценок. Хотя тысячебалльная шкала обладает высокими дифференцирующими возможностями, обычно ее концы оказываются не работающими в силу специального подбора по трудности заданий теста для приближения частотных распределений оценок трудности к виду нормальной кривой. Поэтому, как правило, оценки испытуемых распределяются в интервале от 200 до 800 баллов. Но даже использование менее протяженного диапазона оценок, чем тысячебалльная шкала, требует специальных профессиональных навыков по интерпретации баллов учащихся. Как осмыслить свой результат, если он, например, равен 570 или 650 баллам? Как отнести его к категории плохих или хороших результатов на столь широком диапазоне баллов? Другое дело, если результат испытуемого составляет 5 или 6 баллов по девятибалльной шкале. Поэтому к растянутым шкалам обычно обращаются профессиональные тестовые службы для массового тестирования в образовании, когда большое число испытуемых требует повышения дифференцирующей способности шкалы. В России при шкалировании данных ЕГЭ была выбрана стобалльная шкала, в которую переводятся оценки выпускников. Конечно, стобалльная шкала — это своего рода компромисс между потребностью в хорошем дифференцирующем эффекте шкалы из-за значительного числа тестируемых во всех регионах и постепенным переходом от пятибалльной шкалы, существовавшей на протяжении многих лет в России, к более растянутым шкалам.
4. Шкалирование результатов тестирования на основе теории IRT
Построение шкалы с помощью современной теории тестов. Рассмотренные в предыдущем разделе шкалы позволяют сопоставить результаты тестирования и служат удобной формой их интерпретации, но они не повышают уровень измерений в силу того, что используют статистический аппарат классической теории тестов. Порядковая шкала сырых баллов испытуемых переходит в порядковую шкалу производных стандартизированных показателей, не позволяющих интерпретировать разность результатов двух испытуемых, выполнявших один и тот же тест. Зарубежные исследования конца 80-х гг. XX в. показали возможность построения интервальной шкалы результатов педагогических измерений в том случае, если для создания теста и шкалирования результатов его выполнения используется теория IRT. Условно процесс шкалирования в IRT можно подразделить на три этапа. Первый предполагает построение шкалы логитов для латентного параметра подготовленности испытуемых, второй — шкалы логитов для оценок латентного параметра трудности заданий. Третий этап позволяет свести две шкалы в общую шкалу стандартных оценок для обоих латентных параметров. Связь шкалы логитов и шкалы Гуттмана. Процедура построения шкалы латентных переменных связана с так называемым шкалированием по Гуттману (Guiiman — type scale), в которой задания отбираются в порядке нарастания их трудности по определенным, тщательно структурированным элементам содержания дисциплины. Отличительной особенностью шкалы Гуттмана является существование стойкого кумулятивного эффекта, означающего, что любой испытуемый с правильной структурой знаний, справившийся с j-м заданием, может наверняка успешно выполнить все предыдущие, более легкие задания теста. В понимании Гуттмана совершенная шкала существует в том случае, если по последнему правильному ответу испытуемого можно воспроизвести все его ответы на более легкие задания теста. Конечно, стойкий кумулятивный эффект наблюдается далеко не всегда. В основном он характерен для заданий, довольно тесно связанных по содержанию. Для иллюстрации идей Гуттмана в англоязычной методической литературе популярен следующий пример заданий на умножение:
Он вполне ясно, хотя и довольно упрощенно, показывает, как реализуется эффект кумулятивности на практике. Действительно, если испытуемый умеет умножать на четырехзначное число, то он тем более справится с умножением на трех-, двух- и однозначные числа. Шкалирование на основе теории IRT в определенной степени преодолевает ограниченность предположении шкалы Гуттмана, поскольку является вероятностной версией и отражает сущность тестовых процессов, неизбежно связанных с ошибками. измерения. Согласно моделям IRT о правильном выполнении любого задания испытуемым, можно прогнозировать успешность лишь в том слунае, если эта вероятность близка к единице. Преимущества и проблемы шкалирования по теории IRT. Инвариантность оценок параметров испытуемых относительно трудности заданий теста, достигаемая благодаря, возможностям IRT, позволяет реализовать эффект специфической объективности, который способствует Повышению точности оценок параметра подготовленности учащихся. Благодаря единой шкале интервального типа в IRT разности оценок латентных параметров испытуемых приобретают вполне интерпретируемый смысл, поскольку их можно считать мерой отличия в подготовленности испытуемых по предмету. Таким образом, теория IRT повышает возможности педагогической интерпретации шкалированных баллов, учащихся. С ее помощью можно сопоставить приращения в обученности учащихся и повысить надежность их оценок по тесту. Однако реализовать преимущества теории IRT довольно сложно. Для этого необходимо обеспечить выполнение ряда условий ее применимости, без которых эффект инвариантности не имеет места. В частности нужно обеспечить конструирование теста на основе теории 1RT, подтвердить соответствие эмпирических данных тестирования требованиям моделей измерения или удалить неподходящие данные по результатам выполнения теста. Необходимо также обеспечить нормальный характер распределения сырых баллов учащихся, оценок трудности заданий теста, ошибок измерения и реализовать требование локальной независимости отдельных заданий теста. Немало проблем вызывает расходимость итерационных процессов, работающих в методе максимального правдоподобия при переходе от начальных оценок к наиболее эффективным оценкам параметров испытуемых и трудности заданий теста. Поэтому теория IRT в шкалировании используется далеко не всегда, только в случаях массового тестирования для принятия административно-управленческих решений в образовании, когда есть смысл тратить силы на разработку и применение теста. Преобразования шкалы логитов. Поскольку оценки параметров подготовленности учащихся и трудности заданий теста в шкале логитов обычно лежат в интервале (-5; 5) и имеют несколько знаков после запятой, они малопригодны для сообщения испытуемым без приведения к целому неотрицательному виду. Поэтому необходимы линейные преобразования оценок в другую, более удобную для сообщения результатов шкалу подобно тому, как это происходит с z-оценками. Сначала все значения параметров умножают на один и тот же множитель для перевода результатов в область целых чисел и округляют результат, до целых. Затем переносят все значения параметров на множество положительных чисел путем прибавления некоторой константы, определяющей новую точку отсчета на шкале, для того чтобы избавиться от отрицательных оценок параметра подготовленности θ. Примеры таких преобразований приведены в специальной литературе по шкалированию результатов педагогических измерений.
5. Шкалирование в критериально-ориентированном тестировании
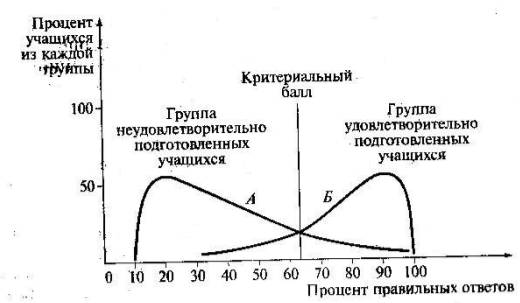
Виды шкал в критериально -ориентированном тестировании. Виды шкал в критериально-ориентированном тестировании выбираются в зависимости от предназначения теста. Если тесты используются для оценки степени освоения содержательной области (domain-referenced tests), отображение которой в тесте условно можно принять за 100%, то каждый балл учащегося показывает процент освоенного содержания. Процесс шкалирования осуществляется достаточно просто балл, набранный учащимся, делят на максимально возможный балл по тесту и полученную величину умножают на 100 %. Упорядочение найденных результатов и их нанесение на ось позволяют построить шкалу, каждая точка которой соответствует проценту усвоенного содержания для учащегося или группы учеников. В другом случае, когда критериально-ориентированный тест применяется для деления тестируемых на две или несколько групп с помощью порогового (критериального) балла (mastery test), строится номинальная шкала. Например, подобное деление происходит при аттестации: в одну группу попадают аттестованные, а в другую — не аттестованные учащиеся, как не выполнившие запланированный процент заданий теста. Основная трудность при таком шкалировании заключается в установлении порогового бапла для отсечения группы учащихся, не показавшей достаточного владения содержанием теста. Методы выбора критериального балла. Для установления порогового балла используются три метода. В первом случае балл устанавливается экспертным путем, априорно, на основе анализа целостного содержания теста. Во втором случае эксперты выбирают пороговый балл на основе анализа .содержания тестовых заданий и присвоения им априорных оценок трудности, с помощью которых выделяется критерий отбора в группу аттестованных учащихся. В третьем случае для определения порогового балла анализируются эмпирические данные по результатам апробации теста на репрезентативной выборке учащихся, и используется метод контрастных групп. Для получения валидного значения критериального балла третьим методом прежде всего необходимо Провести предварительное тестирование на близком по содержанию входном претесте или отобрать группу экспертов, хорошо представляющих, подготовленность тестируемой выборки учащихся. По результатам претеста или экспертизы из группы учащихся выделяются две контрастные подгруппы: заведомо не готовых к тесту самых слабых — 27 % и 27 % самых сильных, хорошо подготовленных к тестированию. В совокупности получаются две контрастные по подготовленности выборки учеников. Затем каждой подгруппе (слабой и сильной) выдается критериально-ориентированный тест, распределение баллов по которому строится на одном графике отдельно для слабых и сильных учащихся (сглаженные кривые — рис. 34, экспериментальные кривые — рис. 35).
Рис. .34. Сглаженные частотные распределения баллов по тесту для контрастных подгрупп
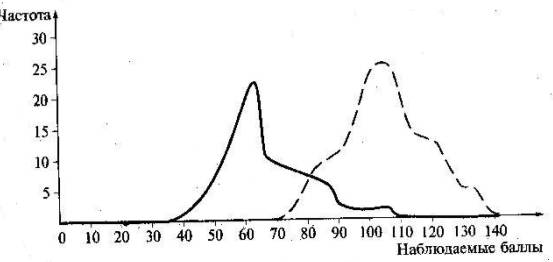
Рис; 35. Эмпирические частотные распределения баллов по тесту для контрастных подгрупп
После проведения тестирования на репрезентативной выборке учащихся и построения частотных распределений для контрастных групп устанавливается критериальный балл в точке, соответствующей на горизонтальной оси пересечению кривых распределения баллов. Эта точка пересечения, спроецированная на рис. 35 на горизонтальную ось, наиболее четко разделяет группы не аттестованных и аттестованных учащихся, поскольку в ней наблюдается наименьший процент ошибочных решений — одновременно минимизируется число учащихся, обладающих достаточно высокой подготовкой, но попавших в группу не аттестованных (часть кривой А слева от вертикальной прямой) и число неподготовленных учеников, ошибочно отнесенных к категории прошедших за пороговый балл (часть кривой В справа от вертикальной прямой). Полученный пороговый балл обладает наибольшей достоверностью по сравнению с его аналогами, определенными экспертными методами. Уровневые шкалы, совмещающие нормативно-ориентированный и критериально-ориентированный подходы. Для получения надежных и обоснованных результатов итоговой аттестации выпускников учебных заведений тестовый балл иногда дополняют развернутой содержательной интерпретацией, описывающей характеристики уровня подготовки учащегося в терминах освоенных элементов содержания. Такие шкалы, позволяющие совместить интерпретацию оценки испытуемого по отношению к результатам остальных тестируемых и к уровням освоения содержания, выделенным по критериальному принципу, получили название уровневых. Пример уровневой шкалы приведен на рис. 36, на котором диапазоны тысячебaлльной шкалы, выбранные гипотетически, соотносятся с уровнями подготовки.
На рисунке выделен базовый и промежуточный уровни вместе с уровнем высокой компетентности. Для построения уровневой шкалы обычно шкалируют результаты репрезентативной группы учащихся в рамках нормативно-ориентированного подхода и строят стандартизованную шкалу тестовых баллов. Затем на шкале выделяют диапазоны и выявляют совокупности содержательных элементов, освоенных учащимися в каждом диапазоне, дополняя детальным описанием освоенных знаний и умений.
6. Рейтинговые шкалы
Упрошенная трактовка рейтинговой шкалы. В российской системе высшего и среднего образования нет устоявшихся определений, позволяющих однозначно определить рейтинговый, балл учащегося. В основном под ним понимают накопленный балл, полученный в результате простого или взвешенного суммирования оценок в порядковых шкалах, которые строятся на основе субъективного выставления и учета баллов учащегося в соответствии с различными уровнями учебной деятельности, временными промежутками в обучении или уровнями усвоения. Нередко к сумативным оценкам, характеризующим успеваемость, прибавляют поощрительные баллы за своевременную: сдачу заданий, активность на занятиях, хорошую посещаемость и т.д. Такая упрощенная трактовка, далекая от педагогических измерений, таит в себе, по меньшей мере, две серьезные ошибки: во-первых, операция суммирования является недопустимой на порядковом уровне измерений и, во-вторых, происходит бессмысленное объединение баллов по различным переменным, что исключает возможность какой-либо корректной интерпретации результатов подобного объединения. Вполне возможна ситуация, когда в. сумме баллов, накопленной учащимся за определенный период обучения, будут доминировать оценки по второстепенным переменным, не имеющим заметного отношения к целям образования. Таким образом, за видимой простотой операции получения рейтингового балла скрывается серьезная опасность: по результатам обучения могут быть признаны лучшими те учащиеся, которые не обладают творческим мышлением, но вовремя сдают домашние задания, не пропускают уроков и не нарушают дисциплины в классе. Обращение к рейтинговой шкале в связке с контрольными заданиями для модулей, построенным на деятельностной основе в русле идей модульного обучения, немного повышает корректность приведенной выше упрощенной трактовки. По крайней мере выделение модулей происходит на содержательной основе и позволяет накапливать оценки уровней усвоения конкретных предметных знаний, что способствует обоснованной интерпретации суммарной оценки. В целом рейтинговые баллы при корректном подходе к их подсчету и интерпретации могут оказать позитивное влияние на контрольно-оценочную систему в образовании. Они способствуют систематической работе учащихся, снижают роль случайности при сдаче экзаменов и снимают нервное напряжение во время экзаменов благодаря заблаговременному накоплению оценок результатов обучения. Корректный подход к построению рейтинговых шкал на основе теорий педагогических измерений. Для корректного построения рейтинговых шкал необходимо выполнять ряд условий. В зарубежной литературе к ним относят: - концептуальное выделение переменных измерения; - использование тестов с высокой содержательной и конструктной валидностью для получения баллов учащихся по каждой переменной; - построение отдельных рейтинговых шкал для каждой переменной измерения; - интеграцию результатов по отдельным шкалам (количественного характера) в единую рейтинговую шкалу с использованием весовых коэффициентов, определенных с помощью регрессионного анализа и методов выравнивания шкал для тестов различной длины при последующем объединении взвешенных количественных баллов по отдельным шкалам. В целом необходимо отметить, что построение рейтинговых шкал требует от учителя определенной методической подготовки, наличия тестов и систематической работы по корректному построению отдельных шкал. При этом повышается нагрузка педагога, поэтому обманчивая простота рейтингования на деле при правильном подходе оборачивается значительными трудозатратами: Под вопросом остается общий эффект, поскольку пока неясно, оправданны ли такие затраты энергии со стороны педагогов или нет.
|