Уравнение бегущей волны

        Уравнение плоской одномерной синусоидальной волны:

        (Вместо синуса можно написать косинус.) Это уравнение отличается от уравнения синусоидальных колебаний тем, что колеблющая величина S зависит не только от времени, но и от координаты. Это и понятно: вместо одного маятника мы имеем множество связанных маятников - частиц среды. v - скорость распространения волны, А - амплитуда волны, аргумент синуса - фаза волны, j₀ - начальная фаза колебаний в точке х = 0, w - частота (циклическая) волны.

        Расстояние, на которое распространяется волна за время, равное периоду колебаний, называется ДЛИНОЙ ВОЛНЫ l = nT.

        ВОЛНОВОЕ ЧИСЛО k:

        С помощью введенного волнового числа уравнение волны запишется:

        Если мы рассматриваем не одномерную волну, удобно наряду с волновым числом ввести ВОЛНОВОЙ ВЕКТОР k, модуль которого равен волновому числу, а направление совпадает с направлением луча (направлением распространения волны). В векторном виде уравнение волны будет выглядеть так:

здесь r - радиус вектор точки пространства; j₀ - начальная фаза колебаний в начале координат.

     Уравнение сферической волны отличается тем, что амплитуда волны убывает с расстоянием от источника:

A₀ = const по смыслу формулы есть амплитуда волны на единичном расстоянии от источника.

        Уравнение волны в дифференциальной форме обычно называют волновым уравнением; вид этого уравнения следующий:

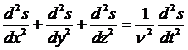     или    

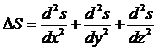
        Уравнение синусоидальной волны является решением волнового уравнения (можно проверить подстановкой). Общее же решение волнового уравнения следующее:

        Здесь А и В - произвольные константы, а f₁ и f₂ - произвольные дважды дифференцируемые функции. Первое слагаемое описывает волну, распространяющуюся слева направо, второе - встречную волну.