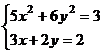Министерство образования  Российской Федерации

ТОМСКИЙ  ГОСУДАРСТВЕННЫЙ  УНИВЕРСИТЕТ  СИСТЕМ  УПРАВЛЕНИЯ  И  РАДИОЭЛЕКТРОНИКИ (ТУСУР)

 

 

 

 

 

С.Л. Миньков

 

 

 

 

 

EXCEL

 

 

Лабораторный практикум

 

 

 

 

 

 

 

 

 

 

 

 

2000

 

 

 

 

Миньков С. Л. Excel: Лабораторный практикум. – Томск: ТУСУР, 2000. –109 с.

 

 

Лабораторный практикум предназначен для изучения электронных таблиц Excel – пакета прикладных программ, широко применяющегося для автоматизации операций обработки данных при решении различных экономических задач.

В 12 лабораторных работах последовательно рассматриваются следующие темы: заполнение таблиц, визуализация табличной информации, обработка статистических данных, составление сводных и отчетных ведомостей, применение формул финансовой математики, решение линейных и нелинейных уравнений и систем, решение дифференциальных уравнений, решение оптимизационных задач.

Практикум рассчитан на студентов очных и заочных отделений вузов, изучающих дисциплины блока «Информатика», а также аспирантов и слушателей факультетов повышения квалификации экономических специальностей. Возможно использование в дистанционном обучении по специальности  «Прикладная информатика (в экономике)».

 

 

 

 

 

 

 

 

 

 

 

 

Ó С.Л. Миньков, 2000

Вводя в ячейку формулу недрогнувшей рукой,

Запомни, юзер, истину простую:

Связавшись с Microsoft, ты потерял покой,

Зато с Excel поймаешь рыбку золотую.

User’ ский фольклор

Введение

 

В 1979 году выпускник Гарвардского университета Дэн Бриклин и профессиональный программист Боб Франкстон предложили миру способ автоматизации трудоемких и утомительных операций пересчета, которые всегда требуются при ручном составлении таблиц в бухгалтерском и банковском учете, в проектно-сметных работах, при решении планово-экономических задач. Это была программа VisiCalc[1], которая позволяла представлять данные в виде таблицы на экране дисплея, прокручивать эту электронную таблицу  по строкам и столбцам и, самое главное, обладала удивительным свойством – в таблице проводился автоматический пересчет содержимого ячеек при изменении значений одной из них. Причем все действия были очень наглядны – всё выполнялось в соответствии с принципом WYSIWYG («What You See Is What You Get»).

Популярность этой программы была феноменальной. Естественно, в первую очередь ею заинтересовались представители делового мира, что, кстати, заметно стимулировало продажу персональных компьютеров. По некоторым оценкам, более четверти проданных машин Apple II в 1979 году покупались для того, чтобы получить возможность работать на VisiCalc. Компьютер превратился в неотъемлемый инструмент бизнеса.

Успех первой электронной таблицы вызвал множество подражаний и вариантов, сопровождавшихся шумными судебными разбирательствами. В конце концов, на рынке программного обеспечения осталось несколько программных продуктов, в числе которых – Excel[2] корпорации Microsoft, входящий в состав интегрированного пакета прикладных программ Microsoft Office for Windows[3].

Excel предлагает широкий набор функциональных средств по обработке табличных данных:

создание и редактирование электронных таблиц с применением богатого набора встроенных функций;

оформление и печать электронных таблиц;

построение диаграмм и графиков различной степени наглядности и детализации;

работа с электронными таблицами как с базами данных: фильтрация, сортировка, создание итоговых и сводных таблиц, консолидация данных из различных таблиц, в том числе из внешних баз данных;

решение экономических задач типа «что – если» путем подбора параметров;

решение оптимизационных задач;

численное решение разнообразных математических задач;

статистическая обработка данных;

использование интегрированной среды разработки собственных программ – макросов на основе языка программирования Visual Basic for Applications.

Предлагаемый цикл из 12 лабораторных работ предназначен для ознакомления с основами Excel и ориентирован на студентов экономических специальностей вузов. Он может быть использован при изучении дисциплин «Информатика», «Разработка и применение пакетов прикладных программ в экономике», а также «Численные методы» – в качестве иллюстративного материала, демонстрирующего возможности офисных пакетов прикладных программ по решению уравнений.

Изучение возможностей Excel основано на версии Excel 97 (или Excel 8), входящего в состав MS Office 97 для Windows 95. Можно также использовать Excel 7.0, входящий в состав MS Office 95, и Excel 2000 из MS Office 2000 Pro.

Лабораторные работы содержат теоретический материал, необходимый для выполнения заданий, примеры, показывающие применение функций Excel, и варианты для самостоятельной работы различной степени сложности. В заключение приведена литература [1-5], которая была использована для подготовки контрольных вариантов.

Лабораторная работа 1. Изучение основ Excel.

Заполнение таблиц

 

Электронная таблица Excel – одна из составных частей пакета прикладных программ Microsoft Office, работающего в среде Windows. Она предназначена для обработки числовых данных, проведения математического моделирования различных процессов (в первую очередь экономических), изготовления различных документов и форм, а также может быть использована в качестве простой базы данных.

 

Книги и листы. При запуске Excel открывается рабочая книга Excel (так называются файлы Excel), которая по умолчанию имеет имя Книга1.xls. Эта книга состоит из трех листов – Лист1, Лист2 и Лист3. Щелкая левой клавишей по ярлычку листа, можно переходить из одного листа в другой. Можно дать им и более осмысленное название. 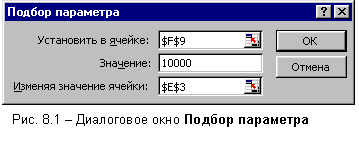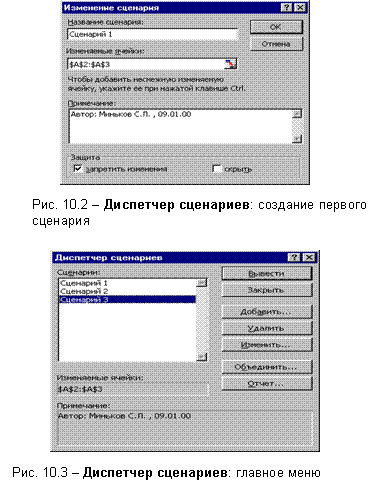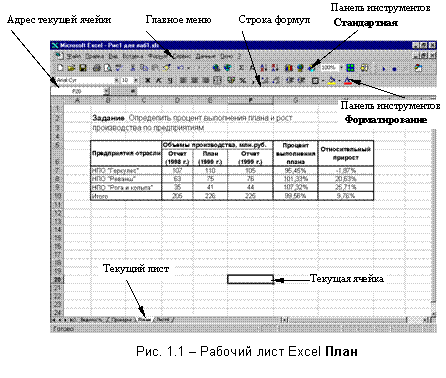Для этого необходимо щелкнуть по ярлычку листа правой клавишей мыши, вызвав контекстно-зависимое меню, выбрать опцию Переименовать и набрать с клавиатуры новое имя, например, «План» (рис.1.1). Отметим, что с помощью предлагаемого меню можно также производить удаление листа, добавление нового листа и перемещение его в другой файл. Есть и другой способ переименования – двойной щелчок левой клавишей мыши по ярлычку листа и набор нового имени.

 

Ячейки. Каждый лист Excel представляет собой таблицу. Столбцы обозначены буквами от A до Z и далее сочетаниями букв от AA до IV, а строки – числами от 1 до 65536 ( в Excel 97). Поэтому каждая ячейка таблицы имеет свой номер, например, А1, GA200. С помощью мыши или клавиш передвижения курсора (указателя)  можно перемещаться из ячейки в ячейку.

Текущая ячейка выделяется черным контуром (F20, рис.1.1). Чтобы выделить несколько ячеек (блок), необходимо щелкнуть левой клавишей мыши по начальной (обычно левой верхней) ячейке и, не отпуская ее, протащить указатель до последней (правой нижней) ячейки. Выделенные ячейки (кроме первой) затемняются. Для выделения нескольких несмежных блоков (бывает полезно при построении диаграмм и графиков) необходимо выделить первый блок, а затем, нажав и удерживая клавишу Ctrl, выделить следующий блок и т.д. Чтобы отменить выделение, достаточно щелкнуть мышью по любому невыделенному участку листа.


Данные. В ячейки таблицы можно вводить три типа данных: текст, число, формулу. По первому символу Excel определяет, что введено: если это буква или апостроф, то это текст, если цифра, то число, если знак равенства, то формула. Для ввода данных необходимо переместиться в нужную ячейку, набрать данные и нажать Enter или клавишу перемещения курсора.

Если текст не входит в ячейку, то можно:

-         раздвинуть границы ячеек по горизонтали, встав курсором на границу между буквами столбцов (широкий крест курсора превращается в черный крестик со стрелками) и, удерживая нажатой левую клавишу мыши, сдвинуть границу на требуемое расстояние;

-         объединить  несколько  ячеек и в них записать текст.  Для этого необходимо выделить несколько соседних ячеек и выбрать через Главное меню Excel путь: Формат | Ячейки (появляется диалоговое окно Формат ячеек, рис. 1.2) | Выравнивание | Объединение ячеек (этот же путь можно выбрать через контекстно-зависимое меню);

-         организовать перенос текста в ячейке по словам: Формат | Ячейки | Выравнивание | Переносить по словам.

Если число не входит в ячейку, то Excel отображает его либо в экспоненциальной форме (1230000000 ® 1,23Е+09), либо вместо числа ставит знаки ####. Тогда необходимо раздвинуть границы ячейки. В Excel можно выбрать различные форматы представления чисел: Формат | Ячейки | Число | Числовые форматы.

 


В виде формулы в ячейке записывается арифметическое или логическое выражение, состоящее из чисел, адресов ячеек и функций, соединенных между собой знаками арифметических операций и операций отношения, и начинающееся со знака =. При его записи следует соблюдать обычные правила алгоритмических языков: арифметические операции выполняются слева направо в порядке старшинства (возведение в степень ^ , умножение *, деление /, сложение +, вычитание -). Для изменения порядка выполнения операций используются круглые скобки, аргумент функции также берется в круглые скобки. Адреса  ячеек набираются только латинским шрифтом!

Двойной щелчок левой клавишей мыши на ячейке с введенными данными осуществляет переход в режим редактирования данных. При этом указатель приобретает вид вертикальной линии.

Переход в режим редактирования данных также можно осуществить щелчком по строке формул.

Для того, чтобы переместить данные, следует выделить ячейку или блок, поместить курсор на рамку ячейки или блока (при этом курсор примет форму светлой стрелки), нажать левую клавишу мыши и, удерживая ее, переместить ячейку или блок в требуемое место. Копирование данных производится аналогично перемещению, но с нажатой клавишей Ctrl .

Аналогичные действия можно провести с помощью контекстно-зависимого меню или через Главное меню Excel (опция Правка).

 

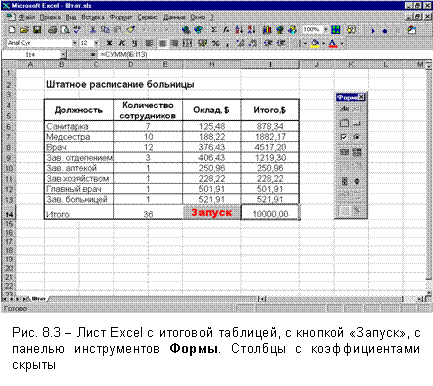
Пример. Рассмотрим применение некоторых возможностей Excel  на примере создания таблицы выполнения плана (см. рис.1.1).

1.       В ячейку В2 вводим текст «Задание. Определить процент выполнения плана и рост», в ячейку В3 – текст «производства по предприятиям». Изменять ширину ячеек нет смысла, т.к. в соседние ячейки текст не вносится и ничто не помешает его увидеть полностью.

2.       Объединяем ячейки В5:С6 и вводим текст «Предприятия отрасли», центрируя его (Формат | Ячейки | Выравнивание | По вертикали (По горизонтали) | По центру).

3.       Объединяем ячейки D5:F6 и вводим текст «Объем производства, млн. руб.». Аналогично, объединяем G5:G6 – текст «Процент выполнения плана», и Н5:Н6 – текст «Относительный прирост». В последних двух блоках также задаем режим Переносить по словам. Передвигая границы ячеек, добиваемся требуемого расположения текста в ячейках.

4.       Объединяя ячейки В7:C7 и т.д., вводим названия предприятий, а в ячейки D6, E6, F6 – текст «План...», «Отчет...».

5.       Заполняем ячейки D7:F9 входными данными.

6.       Заполняем строку «Итого». В ней должен находиться результат суммирования трех вышестоящих ячеек. Суммирование можно выполнить двумя способами.

Первый способ. Выделяем ячейку D10 и выбираем Вставка | Функция | (появляется окно Мастер функций (рис. 1.3)) | Категория | Математические | Функция | СУММ | ОК. В появившемся окне задаем диапазон суммирования D7:D9. После нажатия кнопки ОК в ячейке D10 появляется результат суммирования содержимого ячеек D7:D9. Сама формула

=СУММ (D7:D9)

высвечивается в строке формул.

Окно Мастер функций также открывается щелчком по кнопке со знаком fx на панели инструментов Стандартная. Excel содержит большое количество встроенных функций: математических, статистических, финансовых и других, сгруппированных по категориям (рис. 1.3).


Знание и умелое применение этих функций облегчает процесс обработки информации. Более подробную информацию о каждой функции можно найти в справке по MS Excel : ? | Вызов справки | Предметный указатель; в Поле 1 ввести слово «функция» и выбрать в Поле 2 необходимую функцию.

Второй способ. Выделяем ячейки D7:D9 и щелкаем по кнопке  со  знаком  S  на  панели  инструментов  Стандартная. В ячейке D10 появляется результат суммирования.

7.       Копируем полученную формулу в ячейки E10 и F10. Для этого указываем на маленький квадратик в правом нижнем углу ячейки D10 (курсор при этом превращается в черный крестик – маркер заполнения), нажимаем левую кнопку мыши и, не отпуская ее, двигаем мышь вправо, пока рамка не охватит ячейки E10 и F10. В ячейке Е10 появится формула

=СУММ (Е7:Е9),

а в ячейке F10 – формула

=СУММ (F7:F9).

Таким образом, при копировании произошла автоматическая замена адресов в формуле. Это очень полезное свойство Excel, позволяющее заметно упростить рутинные операции по вводу формул.

Если же при копировании требуется оставить неизменным адрес какой-нибудь ячейки (или только столбца, или только строки), то перед именем столбца и/или номером строки ставится символ $. Например, $D$5, H$4, $A2.

8.       Заносим в ячейку G7 формулу

=F7/E7,

а в ячейку H7 – формулу

=(F7-D7)/D7.

9.       Выделяем ячейки G7 и H7 и копируем сразу две формулы на ячейки G8:G10 и F8:F10, соответственно.

10.   Чтобы задать процентный формат чисел в ячейках G7:H10, можно, выделив их, выбрать путь Формат | Ячейки | Число | Числовые форматы | Процентный ; Число десятичных знаков | 2. Это же самое выполняется быстрее при помощи кнопки Процентный формат панели инструментов Форматирование. Если число десятичных знаков меньше (или больше) требуемого, то следует использовать кнопку Увеличить разрядность (Уменьшить разрядность). Таблица заполнена.

11.   Оформим таблицу, нарисовав внутренние и внешние рамки: Формат | Ячейки | Границы, или используя кнопку Границы на панели инструментов Форматирование.

12.   Можно также подобрать для разных частей таблицы различный фон (тип штриховки, цвет штриховки, цвет фона): Формат | Ячейки | Вид, или используя кнопки Цвет заливки и Цвет шрифта на панели инструментов Форматирование.

Для переноса формата одной ячейки на другую удобно пользоваться кнопкой Формат по образцу на панели инструментов Стандартная. Сначала нужно щелкнуть по «родительской»  ячейке,  затем  по кнопке,  затем по ячейке, куда нужно перенести формат. При этом переносятся все параметры «родительской» ячейки: шрифт, формат числа, цвет, границы и т.п.

 Теперь таблица окончательно готова – и в вычислительном аспекте, и в эстетическом.

При изменении исходных данных в ячейках D7:F9 результаты, находящиеся в ячейках D10:F10 и G7:H10, будут автоматически пересчитываться.

 

Примечание. В Excel существует интересная функция автозаполнения (не использованная в примере), полезная при заполнении рядов данных.

Если ввести в две соседние ячейки последовательно два числа, составляющие начало арифметической прогрессии, например, 1 и 2, затем их выделить и, как при  копировании, с помощью маркера заполнения протащить их на несколько ячеек, то ряд продолжится: 1, 2, 3, 4 и т.д.

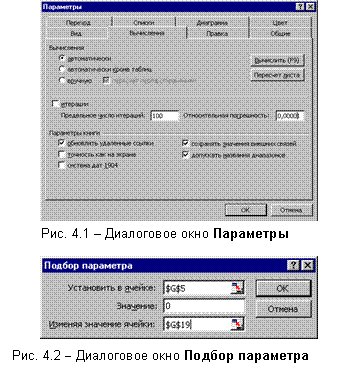
Excel также позволяет вводить и нечисловые последовательности. Например, если ввести в две соседние ячейки Январь и Февраль и осуществить описанную выше операцию, то в следующих ячейках появится Март, Апрель и т.д. Эти последовательности, или списки, можно сформировать самому и дать Excel запомнить их. Для этого необходимо выполнить команду Сервис | Параметры | Списки | Добавить и в окне Элементы списка записать (разделяя Enter) элементы, составляющие список.

 

 

Задание

1.       Открыть файл Excel и разместить на листе таблицу из выбранного варианта.

2.       В позиции, помеченные вопросительным знаком, внести формулы в соответствии с требуемым алгоритмом вычисления. Добавить, если необходимо, новые строки и столбцы.

3.       Оформить таблицу.

 

 

 

 

Вариант 1. Рассчитать суммы распределения прибыли в НПО.

 

Показатели

Нормативы распределения, %

Сумма отчислений прибыли, млн. руб.

Прибыль, всего

Отчисления в бюджет

Отчисления на собственные нужды:

в фонд развития производства

в фонд мат. поощрения

в фонд соц. развития

100

29

 

45

15

11

35,4

?

 

?

?

?

 

 

Вариант 2. Выполнить расчет движения материальных ценностей по складу по балансовым счетам 051, 052, 055 (в тыс. руб.).

 

Показатели, тыс. руб.

Номер счета

Всего по складу

051

052

055

Остаток на начало года

Приход за год

Расход за год

Остаток на конец года

в % к началу года

6000

3400

7000

?

?

30

45

55

?

?

1200

960

750

?

?

?

?

?

?

?

 

 

Вариант 3. Рассчитать, какой процент занимают расходы на продукты в общей сумме расходов (коэффициент Энгеля).

 

Виды расходов, руб.

Группа 1

Группа 2

Группа 3

Группа 4

Группа 5

Продукты

370

580

1300

1950

2300

Жилье

88

125

180

200

1400

Комм. услуги

44

60

120

120

120

Одежда

80

220

800

1500

3500

Другие расходы

350

860

1200

2500

4400

Итого

?

?

?

?

?

К-т Энгеля, %

?

?

?

?

?

 

 

 

 

Вариант 4. Определить экономические показатели фирмы «Геркулес» в отчетном периоде.

 

Сегмент рынка

Себестоимость единицы продукции, руб.

Цена единицы продукции, руб.

Объем реализации, тыс. шт.

Затраты на производство, тыс. руб.

Выручка от реализации, тыс. руб.

Прибыль, тыс. руб.

A

B

C

D

14

13

14

11

16

15

16

13

10

15

20

10

?

?

?

?

?

?

?

?

?

?

?

?

Итого

?

?

?

?

 

Вариант 5. Рассчитать объем территориального фонда обязательного медицинского страхования в 1997 году и сравнить показатели с 1996 г.

 

Поступления, млрд. руб.

1996 г.

1997 г.

В % к итогу

В % к 1996 г.

Страховые взносы

Платежи на обязательное мед. страхование нераб. населения

Штрафные санкции

Другие поступления

101,48

 

75,03

12,77

10,8

148,88

 

118,32

18,0

16,92

?

 

?

?

?

?

 

?

?

?

Итого

?

?

?

?

 

Вариант 6. Рассчитать среднюю стоимость 1 кв. м общей площади жилых помещений в отдельных городах Западно-Сибирского региона в 1997 г.

 

Рынок жилья,

тыс. руб.

Томск

Новосибирск

Барнаул

Тюмень

Первичный рынок:

- улучш. планировки

- элитные

Средняя цена

Средняя цена по отношению к томской, %

 

2640,4

2576,0

?

 

?

 

3354,6

3000,0

?

 

?

 

3132,0

4127,3

?

 

?

 

2886,5

3523,2

?

 

?

Вторичный рынок:

- низкого качества

- типовые

- улучш. планировки

- элитные

Средняя цена

 

2206,1

2268,7

2505,8

3805,6

?

 

1394,7

1847,5

2176,4

3891,1

?

 

1900,0

1989,2

2126,4

3605,3

?

 

2486,7

2999,0

3150,3

4500,2

?

Средняя цена по отношению к томской, %

 

?

 

?

 

?

 

?

Вариант 7. Рассчитать ежедневный предполагаемый доход от деятельности киносети.

 

Кинотеатры

Вместимость зрительного зала, мест

Средний % посещаемости

Средняя цена билета, руб.

Количество сеансов в день

Доход, тыс.руб.

Родина

Сибиряк

Аэлита

Авангард

700

150

300

500

45

40

60

30

40

30

25

40

4

5

3

5

?

?

?

?

Ср. знач.

?

?

?

?

?

Итого

 

?

 

Вариант 8.  Рассчитать сумму оплаты за электроэнергию за 1-й квартал 2000 года. Определить средний расход электроэнергии за квартал.

 

Дата

Показания счетчика, кВт×ч

Расход электроэнергии

Тариф, руб./кВт×ч

Сумма

Текущее

Предыдущее

5.01.2000 г.

39530

—

—

—

—

9.02.2000 г.

39900

?

?

0,17

?

3.03.2000 г.

40210

?

?

0,12

?

2.04.2000 г.

41500

?

?

0,12

?

Итого к оплате

?

 

Вариант 9. Рассчитать сумму оплаты за услуги водоканала и теплосетей за март 2000 года, если в квартире площадью 71,4 кв. м проживает 4 чел. Каков удельный вес каждого платежа в общей сумме?

 

Вид платежа

Стоимость за единицу услуги (вода – на 1 чел., отопление – на 1 кв. м)

% понижения

Стоимость эконом. обоснованная

Начислено фактически

Долг (+); переплата (-)

Итого

Эконом. обоснованная

С учетом пониж. коэффициента

Вода холодная и канализация

Горячая вода

Отопление

 

36,02

39,92

  7,08

 

?

?

?

 

45

72

76

 

?

?

?

 

?

?

?

 

0

102

-23

 

?

?

?

Итого

?

?

?

?

Вариант 10. Рассчитать сумму оплаты за жилищно-коммунальные услуги за март 2000 года, если в квартире площадью 71,4 кв. м проживает 4 человека. Каков удельный вес каждого платежа в общей сумме?

 

Вид платежа

Стоимость за единицу услуги, руб.

% понижения

Стоимость эконом. обоснованная

Начислено фактически

Долг (+); переплата (-)

Итого

Эконом. обоснованная

С учетом пониж. коэффициента

Тех. обслуж.

Кап. ремонт

Очистка стоков

Вывоз мусора

Лифт

Колл. антенна

1,93

1,72

5,43

2,36

9,78

3,80

?

?

?

?

?

?

58

83

50

 1

62

 3

?

?

?

?

?

?

?

?

?

?

?

?

0

0

0

0

-3,25

3,00

?

?

?

?

?

?

Итого

?

?

?

?

Примечание. Общая стоимость технического обслуживания и капитального ремонта исчисляется исходя из площади квартиры, остальные позиции – по числу проживающих.

 

Вариант 11. Расчет затрат на выработку тепла по котельным МП «ТепТоп» (в тыс. руб.).

 

Статья

Тип котельной

Всего

Газовая котельная

Угольная котельная

1. Материалы

2. Амортизация

3. Вода

4. Электроэнергия

5. Заработная плата с начислениями

6. Топливо

7. Ремонтный фонд

8. Цеховые расходы (11,9% от ст. 10)

9. Общеэксплуатационные расходы (9,1% от ст. 10)

10. Итого затрат по котельным, тыс. руб.

84,2

165,6

607,1

339,3

621,2

1234,5

590,0

?

 

?

?

85,5

337,5

80,8

333,9

3081,0

2194,7

320,6

?

 

?

?

?

?

?

?

?

?

?

?

 

?

?

11. Косвенные затраты

12. Всего затрат по котельным с учетом косвенных

13. Рентабельность (15% ст. 12)

391,5

 

?

?

1709,5

 

?

?

?

 

?

?

14. Итого затрат с учетом рентабельности

?

?

?

15. Доля затрат, %

100

?

?

 

 

Вариант 12. Проанализировать динамику поступления товаров от поставщиков.

 

Поставщики

1998 г., млн. руб.

1999 г.,

млн. руб.

Превышение

В % к 1998 г.

Удельный вес в 1998 г.

Удельный вес в 1999 г.

ООО «Прима»

АОЗТ «Томь»

ЧП «Сантик»

ОАО «Гермес»

Всего

15,5

23,4

0,96

7,5

?

16,9

32,1

1,2

6,4

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

 

 

 

Вариант 13. Составить таблицу начисления заработной платы работникам МП «Воронья слободка».

 

Ф.И.О.

Тарифный разряд

% выполнения плана

Тарифная ставка

Заработная плата с премией

Пряхин Н.П.

Суховейко А.Д.

Лоханкин В.А.

Пферд Л.Ф.

Севрюгов Л.А.

Гигиенишвили Г.С.

Птибурдуков А.И.

3

2

1

1

3

2

3

102

98

114

100

100

94

100

?

?

?

?

?

?

?

?

?

?

?

?

?

?

 

Примечание 1. Тарифная ставка определяется в зависимости от разряда: 1-й разряд – 1200 руб.; 2-й разряд – 1500 руб.; 3-й разряд – 2000 руб.

Примечание 2. Размер премиальных определяется в зависимости от выполнения плана:

- ниже 100% – премия не начисляется;

- 100% – премия 20% от тарифной ставки;

- 101…110% – премия 30%;

- 111…115% – премия 40%.

 

 

 

Вариант 14. Сравнить доходную часть городского бюджета в 1999 и 2000 году.

 

Статья

1999 г. (отчет), тыс. руб.

Удельный вес, %

2000 г. (план), тыс. руб.

Удельный вес, %

Превышение

В % к 1999 г

Налоговые доходы

1. Налоги на прибыль (доход), прирост капитала

2. Налоги на товары и услуги, лицензионные сборы

3. Налоги на совокупный доход

4. Налоги на имущество

5. Платежи за пользование природными ресурсами

6. Прочие налоги, пошлины и сборы

Неналоговые доходы

1. Доходы от имущества, находящегося в гос. собственности

2. Административные платежи и сборы

3. Штрафные санкции

Итого доходов

?

 

347660

 

 

396110

 

53810

266900

 

 

102600

 

236580

?

 

 

10690

 

9500

3500

?

?

 

?

 

 

?

 

?

?

 

 

?

 

?

?

 

 

?

 

?

?

100

?

 

666562

 

 

142887

 

35696

107253

 

 

382380

 

274296

?

 

 

37366

 

4500

3600

?

?

 

?

 

 

?

 

?

?

 

 

?

 

?

?

 

 

?

 

?

?

100

?

 

?

 

 

?

 

?

?

 

 

?

 

?

?

 

 

?

 

?

?

?

?

 

?

 

 

?

 

?

?

 

 

?

 

?

?

 

 

?

 

?

?

?

 

Вариант 15. Рассчитать начисление стипендии студентам по итогам сессии.

 

Ф.И.О.

Оценки за экзамены

Начисление стипендии

Информатика

Эконом. теория

Теория

вероятности

ТЭИС

1. Иванопуло И.П.

2. Зверев Д.Б.

3. Калачов Н.А.

4. Калачова Е.Б.

5. Синицына З.С.

6. Писаревская Л.Г.

7. Тарасов А.Н.

8. Паровицкий С.Т.

5

4

4

4

4

5

3

4

5

4

5

3

5

5

5

4

5

5

5

2

3

4

2

5

5

5

5

4

5

4

4

4

?

?

?

?

?

?

?

?

 

Примечание. Размер стипендии составляет 2 МРОТ (минимальный размер оплаты труда, равный 108 руб. 54 коп.). Если все экзамены сданы на «пятерку», то надбавка составляет 50%. Если есть одна «четверка» (при остальных «пятерках»), то надбавка составляет 25%. Если есть хотя бы одна «двойка», то стипендия не начисляется.

 

Вариант 16. Рассчитать поступление и расходование денежных средств избирательных фондов зарегистрированных кандидатов в депутаты на должность главы администрации.

 

Показатели

Ф.И.О. зарегистрированного кандидата

Полесов В.М.

Чарушников М.П.

Кислярский М.Б.

Сумма, руб.

% к всего

Сумма, руб.

% к всего

Сумма, руб.

% к всего

Поступило средств всего,

в том числе:

от избирательной комиссии

собственные средства кандидата

пожертвования юридических лиц

пожертвования физических лиц

 

?

 

 

2000

 

 

800

 

125000

 

—

 

100

 

 

?

 

 

?

 

?

 

?

 

?

 

 

2000

 

 

800

 

1057300

 

—

 

100

 

 

?

 

 

?

 

?

 

?

 

 

?

 

2000

 

 

2000

 

4193410

 

10590

 

100

 

 

?

 

 

?

 

?

 

?

Израсходовано средств всего,

 в том числе:

радио и телевидение

печатные издания

публичные мероприятия

канцелярские расходы

Аренда помещений и автотранспорта

Прочие расходы

 

?

 

 

—

 

114418

 

—

 

—

 

 

8800

4940

 

100

 

 

?

 

?

 

?

 

?

 

 

?

?

 

?

 

 

334122

 

604582

 

7780

 

4169

 

 

14392

30231

 

100

 

 

?

 

?

 

?

 

?

 

 

?

?

 

?

 

 

752600

 

1332990

 

200330

 

106040

 

 

95170

1172180

 

100

 

 

?

 

?

 

?

 

?

 

 

?

?

Остаток неизрасходованных средств

?

?

?

Вариант 17. Рассчитать доход от реализации колбасных изделий АОЗТ «Рога и копыта».

 

Наименование

изделий

Объем производства, т

Цена за кг, руб

Торгово-сбытовая скидка, %

Цена со скидкой

Сумма

Колбаса пермская п/к, 1с.

Колбаса одесская п/к, 1с.

Колбаски охотничьи, п/к, в/с,

Колбаса польская п/к, 2с.

Колбаса таллиннская п/к, в/с.

 

5

 

12

 

2

 

14

 

3

 

50

 

60

 

79

 

46

 

66

 

8

 

8

 

8,5

 

7,8

 

8,5

 

?

 

?

 

?

 

?

 

?

 

?

 

?

 

?

 

?

 

?

Всего

?

 

 

 

?

 

Вариант 18. Рассчитать заработную плату работникам высшего учебного заведения.

 

Ф.И.О.

Оклад (штат.), руб.

Начислено по окладу

Надбавки

Удержано

Всего начислено

Всего удержано

Сумма к выдаче

За ученую степень (в МРОТ)

Персональная (в% от гр.2)

Остальные (в % от гр.2)

Подоходный налог (12% от гр. 10)

Пенсионный налог (1% от гр. 10)

Профсоюз (1% от гр. 10)

1

2

3

4

5

6

7

8

9

10

11

12

Штатные

Персицкий Р.

Судейкин М.

Наперников Г

 

660585385

 

?

?

?

 

3

3

—

 

40

40

—

 

20

—

30

 

?

?

?

 

?

?

?

 

?

?

?

 

?

?

?

 

?

?

?

 

?

?

?

Совместители

Ляпис Н.

Авдотьев К.

 

 

405

660

 

 

?

?

 

 

—

1,5

 

 

—

40

 

 

—

35

 

 

?

?

 

 

?

?

 

 

?

?

 

 

?

?

 

 

?

?

 

 

?

?

 

Примечание 1. Надбавка за ученую степень рассчитывается, исходя из минимального размера оплаты труда (МРОТ), равного 108 руб. 54 коп.

Примечание 2. Начисление по окладу (графа 3) составляет 100% для штатных работников и 50% для совместителей.

 

Вариант 19. Рассчитать плановую сумму прибыли ЧП «Московские баранки».

 

Показатели

Год

1999 г в % к 1997г.

1997

1998

1999

1. Объем продаж, т

2. Цена единицы продукции, руб./кг

3. Выручка от реализации продукции, руб.

4. Постоянные расходы, руб.

5. Переменные расходы (60% от ст. 3),  руб.

6. Общая себестоимость продукции, руб.

7. Удельная себестоимость продукции, руб.

8. Валовая прибыль, руб.

30

 

10

 

?

90000

 

?

 

?

 

?

?

47

 

13

 

?

90300

 

?

 

?

 

?

?

62

 

16

 

?

90500

 

?

 

?

 

?

?

?

 

?

 

?

—

 

—

 

?

 

?

?

 

Вариант 20. Оценить влияние изменения расхода материалов на изменение удельной материалоемкости изделия.

 

Материалы

1998 г.

1999 г.

Количество материала, т

Затраты на материалы в ценах 1999 г.

Количество материала, т

Цена 1 кг

материала, У.Е.

Затраты на материалы, У.Е.

1

2

3

4

5

6

Сталь 3Х13

Сталь 12ХР3А

Дюралюминий

Бронза

Латунь

130

126

56

13

34

?

?

?

?

?

165

123

78

12

31

3,4

4,3

4,2

8,7

5,3

?

?

?

?

?

Итого

—

?

—

—

?

Оценка изменения расхода материалов на изменение удельной материалоемкости изделия, DM

?

 

Примечание. Величина DM вычисляется по формуле:

,

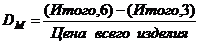где цена всего изделия равна 25 У.Е.

 

Вариант 21. Сформировать и заполнить накопительную ведомость по переоценке основных средств производства (в млн. руб.).

 

Наименование объекта

Балансовая стоимость

Износ

Остаточная стоимость

Восстановительная полная стоимость

Восстановительная остаточная стоимость

Заводоуправление

12556,4

589,3

?

?

?

Диспетчерская

184,0

51,2

?

?

?

Цех №1

954,4

235,1

?

?

?

Цех №2

821,9

218,9

?

?

?

Цех №3

529,6

124,7

?

?

?

Цех №4

758,4

171,1

?

?

?

Склад №1

580,2

223,3

?

?

?

Склад №2

443,9

98,6

?

?

?

Склад №3

579,0

123,4

?

?

?

Склад №4

322,8

69,8

?

?

?

Итого

?

?

?

?

?

 

Примечание 1. Восстановительная полная стоимость (ВПС) объекта  и восстановительная остаточная стоимость (ВОС) объекта вычисляются по балансовой стоимости (БС) и износу объекта (ИО):

ВПС = БС*К;  ВОС = ОС*К,

где  К = 3,0, если БС > 500 млн. руб.;

       К = 2,0, если БС £ 500 млн. руб.

Примечание 2. Для заполнения столбцов использовать функцию ЕСЛИ.

 

Вариант 22. Рассчитать структуру розничной цены продукции (руб.), исходя из следующих данных:

 

Составляющие

Виды продукции

А

В

С

D

1. Себестоимость

2. Рентабельность (25% от п.1)

3. Оптовая цена предприятия

4. Акциз (70% от оптовой цены)

5. Наценка посредника

6. НДС (20% от отпускной цены фирмы)

7. Торговая наценка

8. Розничная цена

 

50

?

?

?

10

 

?

12

?

71

?

?

?

10

 

?

12

?

36

?

?

?

8

 

?

10

?

12

?

?

?

8

 

?

10

?

 

 

 

 

Вариант 23. Рассчитать розничную цену 1 кг хлеба различных сортов, исходя из следующих данных:

 

Составляющие

Сорт

Пшеничный в/с

Пшеничный 1с.

Ржаной в/с

1. Стоимость пшеницы (1 кг), руб.

2. Стоимость ржи (1 кг), руб.

3. Издержки элеваторов, руб

4. Рентабельность затрат элеваторов, %

5. Издержки мельниц, руб.

6. Рентабельность затрат мельниц, %

7. Издержки хлебозаводов, руб.

8. Рентабельность затрат хлебозаводов, %

9. Оптовая цена 1 кг хлеба (при норме выхода продукта 140%)

10. НДС (10% от ст. 9)

11. Отпускная цена 1 кг хлеба с НДС

12. Торговая надбавка, %

13. Розничная цена 1 кг хлеба

 

1,4

—

0,6

15

0,6

20

0,9

20

 

?

?

?

15

?

1,1

—

0,6

15

0,5

20

0,8

20

 

?

?

?

15

?

—

1,5

0,6

15

0,5

20

0,8

20

 

?

?

?

15

?

 

 

 

Вариант 24. Оформить в виде таблицы расчет подоходного налога за 1999 год с пяти физических лиц, чьи доходы лежат в каждой из пяти категорий, по следующему алгоритму:

-      до 30000 руб. : 3% в федеральный бюджет, 9% в бюджет субъектов федерации;

-      от 30001 до 60000 руб. : 3% в федеральный бюджет, 2700 руб. + 12% с суммы, превышающей 30000 руб., в бюджет субъектов федерации;

-      от 60001 до 90000 руб. : 3% в федеральный бюджет, 6300 руб. + 17% с суммы, превышающей 60000 руб., в бюджет субъектов федерации;

-      от 90001 до 150000 руб. : 3% в федеральный бюджет, 11400 руб. + 22% с суммы, превышающей 90000 руб., в бюджет субъектов федерации;

-      от 150001 и выше : 3% в федеральный бюджет, 24600 руб. + 32% с суммы, превышающей 150000 руб., в бюджет субъектов федерации.

Подсчитать итоговые суммы к выплате.

 

Вариант 25. Рассчитать прибыль, полученную от реализации трех видов продукции.

 

Показатель

Продукция

Итого

А

В

С

1. Цена изделия, тыс. руб.

2. Количество изделий, реализуемых в рассматриваемом периоде, шт.

3. Выручка от реализации, тыс. руб.

4. Удельный вес каждого изделия в общем объеме реализации, %

5. Переменные расходы в расчете на одно изделие, тыс. руб.

6. Переменные расходы по каждому виду продукции, тыс. руб.

7. Постоянные расходы в рассматриваемом периоде, тыс. руб.

5

 

500

?

 

?

 

3

 

?

 

—

10

 

700

?

 

?

 

6

 

?

 

—

20

 

300

?

 

?

 

12

 

?

 

—

—

 

?

?

 

100

 

—

 

?

 

6000

8. Итого расходов

9. Прибыль

 

?

?

 

 

 

 

Вариант 26. Рассчитать итоговое количество продукции, произведенное в России различными отраслями за 4 года, и относительные показатели каждого года.

 

Продукция

Года

Итого

1994

В % к 1997 г.

В % к общему итогу

1995

В % к 1997 г.

В % к общему итогу

1996

В % к 1997 г.

В % к общему итогу

1997

Топливно-энергетические отрасли

Электроэнергия, млрд. кВт. ч

Нефть,

млн. т

Газ естественный, млрд. м3

Уголь,

млн. т

 

 

 

 

 

 

876

 

310

 

 

607

 

271

 

 

 

 

 

 

?

 

?

 

 

?

 

?

 

 

 

 

 

 

?

 

?

 

 

?

 

?

 

 

 

 

 

 

862

 

298

 

 

595

 

262

 

 

 

 

 

 

?

 

?

 

 

?

 

?

 

 

 

 

 

 

?

 

?

 

 

?

 

?

 

 

 

 

 

 

848

 

293

 

 

601

 

255

 

 

 

 

 

 

?

 

?

 

 

?

 

?

 

 

 

 

 

 

?

 

?

 

 

?

 

?

 

 

 

 

 

 

834

 

297

 

 

571

 

244

 

 

 

 

 

 

?

 

?

 

 

?

 

?

Черная металлургия, млн. т

Чугун

Сталь

Прокат готовых черных металлов

Трубы стальные

 

 

 

36,1

48,7

 

 

 

36,5

 

3,57

 

 

 

?

?

 

 

 

?

 

?

 

 

 

?

?

 

 

 

?

 

?

 

 

 

39,2

51,3

 

 

 

39,1

 

3,72

 

 

 

?

?

 

 

 

?

 

?

 

 

 

?

?

 

 

 

?

 

?

 

 

 

35,6

49,2

 

 

 

38,8

 

3,50

 

 

 

?

?

 

 

 

?

 

?

 

 

 

?

?

 

 

 

?

 

?

 

 

 

37,3

48,4

 

 

 

37,8

 

3,47

 

 

 

?

?

 

 

 

?

 

?

 

 

Вариант 27. Используя рекламную прессу (газета «Реклама»), проанализировать затраты на рекламу производителей товаров и услуг в Томске по различным направлениям. Стоимость рекламных объявлений в газете «Реклама» (в рублях за 1 кв. см): первая полоса - 29, последняя полоса - 18, полоса с программой ТВ - 15, обычная полоса - 9,8 (эти данные оформить отдельной таблицей и ссылаться на них через адреса ячеек).

 

 

Секторы рынка

Площадь объявлений, кв. см

Затраты на рекламу, тыс. руб.

Место по затратам

Первая полоса

Последняя полоса

Полоса с программой ТВ

Обычная полоса

Информационные технологии и услуги

430,8

135,0

208,8

5363,5

?

?

Продовольственные товары

41,3

0

0

4191,3

?

?

Строительно-хозяйственные товары и услуги

149,3

138,5

488,3

3697,8

?

?

Предметы гигиены и санитарии

0

0

0

949,0

?

?

Одежда и обувь

0

0

108,0

534,5

?

?

Мебель и торговое оборудование

134,0

0

0

2071,3

?

?

Лекарства и медицинские услуги

0

0

42,3

568,0

?

?

Автотовары и автоуслуги

50,0

0

0

2648,1

?

?

Бытовая техника и ее обслуживание

0

420,0

0

1680,3

?

?

Недвижимость

76,3

0

0

2087,3

?

?

Итого

?

?

?

?

?

?

 

 

 

 

 

Вариант 28. Рассчитать сумму, которая будет на счету в конце каждого месяца, если в начале года внесено 10000 руб., для различных годовых норм банковского процента  i.

 

Годовая норма i,%

Период, месяц

1

2

3

4

5

6

7

8

9

10

11

12

?
 
4

5

6

7

8

9

11

15

 

 

 

 

 

 

 

 

 

 

 

 

 

Примечание. Формула для расчета сложных процентов имеет вид:

,

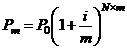где  P0 – первоначально вложенная сумма;

Pm – сумма, которая будет получена через N лет;

m – количество начислений процентных платежей в течение годового периода;

i – годовая норма процента.

 

Вариант 29.  Одним из показателей, определяющих эффективность планируемых инвестиций, является показатель чистой текущей стоимости, вычисляемый по формуле:

,

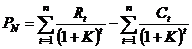где  Rt – доходы  (за вычетом налогов) от реализации проекта в t-ом году , руб.;

Сt – инвестиции в проект в t-ом году, руб.;

К – норма дохода по проекту;

n – период реализации проекта в годах.

Из четырех предлагаемых проектов выбрать наиболее эффективный, используя функцию MAX. Норма доходности инвестиций – 10%. Расчеты оформить в виде таблицы, добавив к таблице исходных данных необходимое число строк или столбцов.

 

Период

1-й проект

2-й проект

3-й проект

4-й проект

Rt

Ct

Rt

Ct

Rt

Ct

Rt

Ct

 

1-й год

 

2-й год

 

3-й год

 

4-й год

 

5-ый год

 

 

0

 

2500

 

3000

 

4300

 

5800

 

 

10000

 

0

 

0

 

0

 

0

 

0

 

2000

 

3200

 

4400

 

6200

 

4000

 

3000

 

2000

 

1000

 

0

 

1000

 

2000

 

3000

 

4000

 

6000

 

3000

 

4000

 

3000

 

0

 

0

 

0

 

0

 

4000

 

6000

 

7000

 

 

1000

 

3000

 

4000

 

1000

 

1000

Чистая текущая стоимость

?

?

?

?

 

Вариант 30. Рассчитать доход, полученный от вложения свободных средств в одно- , трех- и шестимесячные депозиты к концу 6-го месяца. Доход от одномесячного депозита – 1%, от трехмесячного депозита – 4%, от шестимесячного депозита – 9%. Результаты расчета предлагается оформить в виде следующей таблицы.

 

Статьи доходов

(расходов), тыс. руб.

Период, месяц

Итог

1

2

3

4

5

6

Начальная сумма

Погашение депозита

Проценты по депозиту

1-месячный депозит

3-месячный депозит

6-месячный депозит

Собственные расходы

Сумма на конец месяца

500

—

—

50

100

150

30

?

?

?

?

50

—

—

30

?

?

?

?

50

—

—

30

?

?

?

?

50

100

—

30

?

?

?

?

50

—

—

30

?

?

?

?

50

—

—

30

?

?

?

?

—

—

—

30

?

Доход

?

 

Примечание. Процентные ставки по депозитам также оформить в виде таблицы и при ссылке на них использовать адреса соответствующих ячеек.

Лабораторная  работа  2.  Построение  диаграмм  и графиков функций.

 

            С помощью Excel можно превращать сухие и абстрактные строки и столбцы чисел в привлекательные и информативные графики и диаграммы. Визуальное представление информации облегчает ее восприятие, помогает лучше представить поведение функциональных зависимостей.

            Построение графиков и диаграмм осуществляется с помощью Мастера диаграмм. Его вызов производится либо с помощью команды Вставка | Диаграмма, либо щелчком по кнопке Мастер диаграмм в панели инструментов Стандартная.

 

Как построить диаграмму?

Рассмотрим таблицу 2.1, показывающую рост штатного состава подразделений фирмы. Порядок действий следующий.

 

Таблица 2.1 – Штат фирмы «Шмидт и сыновья»

Подразделение

Период

Январь

Октябрь

Офис 1

2

5

Офис 2

7

9

 

1.       Выделяем  таблицу  вместе  с подписями  строк  и столбцов.

2.       Нажимаем кнопку Мастер диаграмм и шаг за шагом проходим все этапы построения диаграммы.

Шаг 1. Выбираем тип диаграммы Гистограмма и вид диаграммы Объемная (рис. 2.1).

Шаг 2. Здесь указывается диапазон ячеек, содержащих данные (рис. 2.2). Так как таблица была заранее выделена, диапазон уже установлен. Проверьте в окне предварительного просмотра, как выглядит диаграмма. Если она не соответствует желаемому, укажите другой диапазон. Отметьте, как расположены данные – в столбцах или строках. Если в строках, то подписями оси Х будут Январь, Октябрь, а категории Офис 1 и Офис 2 уйдут в легенду диаграммы, если в столбцах, то наоборот.

На вкладке Ряд можно указать другие данные для диаграммы, а также удалить или добавить ряды.

 

 


Шаг 3. В этом окне находится шесть вкладок (рис. 2.3), на которых можно изменить параметры выбранного типа диаграммы, например, написать название диаграммы, задать сетку, написать значения (или проценты, доли) над столбцами диаграммы и т.д.


Шаг 4. Здесь указывается место размещения новой диаграммы:  либо  на  имеющемся  листе,  либо на новом листе (рис. 2.4).


После построения диаграммы имеется возможность изменить ее параметры. Для этого достаточно щелкнуть правой клавишей мыши по области построения диаграммы и выбрать в появившемся контекстно-зависимом меню необходимую опцию (обратите внимание, что меню будет иметь разный вид в зависимости от того, по какому месту щелкнуть: или по легенде, или по оси, или по области диаграммы и т.д.).

Существует также удобный способ добавления новых данных к диаграмме: выделить новые данные в таблице и перетащить их на диаграмму. В соответствующем виде они появятся на поле диаграммы.

 

Как построить график зависимости функции одного переменного?

Пусть дана таблица 2.2 зависимости цены единицы некоторого товара от объема его продаж (известная в экономике «кривая спроса D-D»). Сразу отметим: если функция задана аналитической зависимостью y=f(x), то нужно предварительно ее протабулировать, то есть построить таблицу {xi , yi}, где xi=x0 + i×h, h = (xn – x0)/n; i = 0…n, а yi=f(xi). Для заполнения ряда x используется режим автозаполнения.

 

Таблица 2.2 – Спрос

Объем продаж, тыс. шт.

8

10

18

20

32

40

50

Цена, руб.

510

430

350

200

200

100

80

 

Порядок построения графика следующий.

1.       Выделяем всю таблицу и вызываем Мастер диаграмм.

2.       На первом шаге выбираем Тип: Точечная и Вид: Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров. Обращаем ваше внимание на то, что Тип: График не пригоден в данном случае, так как показывает тенденции изменения данных за равные промежутки времени; при этом обе группы данных (х и у) отображаются в виде графиков.

3.       На втором шаге в окне предварительного просмотра проверяем, правильно ли построен график. Обратите внимание: первая строка (или первый столбец, если данные расположены столбцом) воспринимается как данные оси Х , а вторая строка (столбец) или строки (столбцы), если они имеются, как данные оси Y.

4.       Следующие шаги выполняются так же, как описано выше

Результат приведен на рисунке 2.5.

 


Как построить график зависимости функции двух переменных?

Построим график производственной функции Кобба-Дугласа Y=A×KaLb, где А, a, b – константы, K – объем фондов , L – объем трудовых ресурсов, Y – выпуск продукции предприятием или отраслью. Эти переменные могут выражаться либо в стоимостном выражении, либо в натуральном количестве.

Пусть функция имеет вид:

Y=900×K0,5L0,25 ( тыс. руб.),

где K=100 ... 200 тыс. руб.; L=30 ... 50 тыс. руб.

Графическое представление функции двух переменных – поверхность в трехмерном пространстве.

Табулируем функцию, располагая значения K по горизонтали, а L – по вертикали; тогда на пересечении столбца со значением Ki и строки со значением Li будет находиться значение функции Yi .

При наборе формулы необходимо зафиксировать знаком $ номер строки переменной,  изменяющейся  по горизонтали (т.е. K), и номер столбца переменной, изменяющейся по вертикали (т.е. L).

Например, в таблице 2.3 в ячейке В21 находится формула вида

              = 900*B$20^0,5*$A21^0,25

Тогда при копировании формулы на все ячейки таблицы смена адресов для переменных будет проведена корректно (проверьте!).

 

Таблица 2.3 – Элемент листа Excel с табулированием функции двух переменных

 

A

B

C

D

E

...

Значения L

Значения К

 

 

20

 

100

110

120

...

21

30

21063,1

22091,2

23073,5

...

22

35

21890,7

22959,2

23980,1

...

23

40

22633,8

23738,5

24794,1

...

24

...

...

...

...

...

 

Результаты построения приведены на рисунке 2.6.


Порядок построения этой поверхности следующий.

1.       Выделяем всю таблицу: и значения аргументов, и значения функции. Обратите внимание: левая верхняя ячейка выделенной области таблицы (у нас это ячейка А20) должна быть пустая.

2.       Вызываем Мастер диаграмм.

3.       На первом шаге выбираем Вид: Поверхность, Тип: Поверхность

4.       На втором шаге можем предварительно посмотреть построенную поверхность и, при необходимости, изменить ряды данных.

5.       На третьем шаге пишем название диаграммы, название оси Х (категорий) - это горизонтальный ряд данных, т.е. K, название оси Y (рядов данных) - это вертикальный ряд данных, т.е. L, и название оси Z (значений) – это наша функция Y.

6.       На четвертом шаге размещаем построенную диаграмму на выбранном листе.

Обычно после построения требуется отредактировать диаграмму: сменить размер шрифта, фон стенок, размещение надписей и т.д. Для этого надо подвести стрелку к соответствующему объекту, щелкнуть правой клавишей мыши и из контекстно-зависимого меню выбрать соответствующую опцию. Пробуйте, экспериментируйте. Excel предоставляет для этого массу возможностей!

Отметим еще, что, подведя курсор к какому-нибудь углу стенок области построения графика (появится надпись «Углы») и «схватив» мышью этот угол (появится тонкий крестик), можно двигать область диаграммы, рассматривая график в различных ракурсах.

 

Задания

Задание 1. Построить диаграммы, иллюстрирующие табличные данные из лабораторной работы 1. Тип диаграммы выбрать исходя из степени наглядности представления информации. Обязательно включить название, подписи рядов данных, легенду. Разместить диаграмму на отдельном листе.

Задание 2. Построить график функции одного переменного на отрезке хÎ[-2; 2] для одного из выбранных вариантов, приведенных ниже. При записи формулы использовать функцию ЕСЛИ.

1

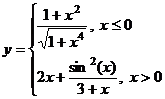
2

 

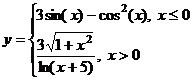
3

 

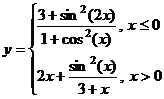
4

 

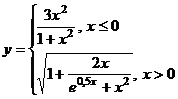
5

 

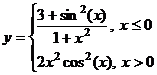
6

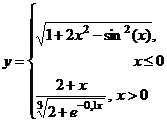
7

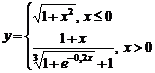
8

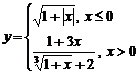
9

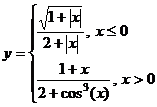
10

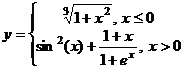
11

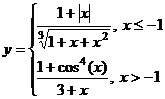
12

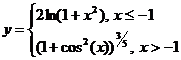
13

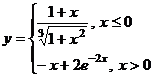
14

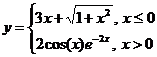
15

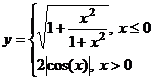
16

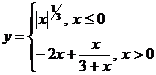
17

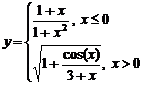
18

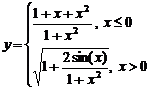
19

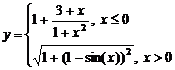
20

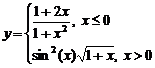
21

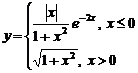
22

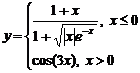
23

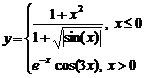
24

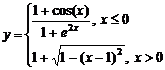
25

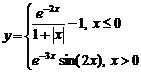
26

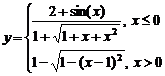
27

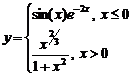
28

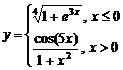
29

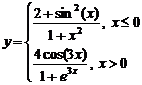
30

 

 

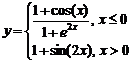
Лабораторная работа 3. Трендовый анализ

 

Excel имеет специальный аппарат для графического анализа моделей, в том числе построения аппроксимационных зависимостей (линий тренда P(x)) по данной таблице {xi , yi}, которые приближенно отражают функциональную связь y=f(x).

Линии тренда обычно используются в задачах прогнозирования. Такие задачи решают с помощью методов регрессионного анализа. С помощью регрессионного анализа можно показать тенденцию изменения рядов данных, экстраполировать их (то есть продолжить линию тренда вперед или назад за пределы известных данных). Можно также построить линию скользящего среднего, которая сглаживает случайные флуктуации, яснее демонстрирует модель и прослеживает тенденцию изменения данных.

Линиями тренда можно дополнить ряды данных, представленные на линейчатых диаграммах, гистограммах, графиках, биржевых, точечных и пузырьковых диаграммах. Нельзя дополнить линиями тренда ряды данных на объемных, лепестковых, круговых и кольцевых диаграммах.

Excel позволяет выбрать один из пяти типов линии тренда – линейный, логарифмический, экспоненциальный, степенной или полиномиальный (2...6 степени) и проверить (по различным критериям), какой из типов лучше всего подходит в данной ситуации. Критерием может служить или критерий R2 (коэффициент детерминации), автоматическое вычисление которого встроено в диалоговое окно Линия тренда, или квадратичное отклонение

,

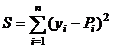обычно используемое в методе наименьших квадратов при аппроксимации табличных функций.

Чем меньше квадратичное отклонение, тем лучше линия тренда аппроксимирует ряд данных. Или, чем ближе коэффициент детерминации к единице, тем лучше тренд.

 

 

 

Задания

Задание 1. Используя статистические данные по численности населения России (таблица 3.1), построить линейный график ЧислСтат (Год). Выделив линию графика, построить различные линии тренда, выражающие зависимость численности населения от времени: Вставка | Линия тренда (или, наведя курсор на линию графика, щелкнуть правой клавишей мыши; в появившемся контекстно-зависимом меню выбрать Добавить линию тренда).

 

Таблица 3.1 – Население России

Год,

t

Численность

статист.,

млн. чел.

Теория

y=k*t+m

C-T

Теория

y=a*t^2+d*t+c

C-T

Теория

y=a*exp(b*t)

С-Т

Теория

y=c*t^n

C-T

1960

117,5

 

 

 

 

 

 

 

 

1970

130,1

 

 

 

 

 

 

 

 

1980

137,6

 

 

 

 

 

 

 

 

1990

147,4

 

 

 

 

 

 

 

 

1991

148,5

 

 

 

 

 

 

 

 

1992

147,7

 

 

 

 

 

 

 

 

1993

148,7

 

 

 

 

 

 

 

 

1994

148,4

 

 

 

 

 

 

 

 

1995

148,3

 

 

 

 

 

 

 

 

2000

?

 

 

 

 

 

 

 

 

 

 

S1=

 

S2=

 

S3=

 

S4=

 

 

Проверить линейную, полиномиальную (n=2), экспоненциальную, степенную линии: Тип | Построение линии тренда (рис. 3.1).

Для каждого тренда:

а) выдать аналитическую зависимость Численность (Год): Параметры | Показывать уравнение на диаграмме (рис. 3.2);

б) найти погрешность С–Т (разницу между статистической и трендовой численностью);

в) рассчитать квадратичное отклонение Si , используя функцию СУММКВ.

Сравнить эти отклонения и по минимальному Si оценить численность населения в 2000 году.

 

 

 


 

 

 

 

Задание 2. Используя новое значение численности России в 1998 году – 146,2 млн. чел., уточнить экстраполяцию, используя только данные 90-х годов. Проанализировать полученные результаты.

 

Задание 3. По заданной таблице 3.2 построить линии полиномиального тренда, наилучшим образом (по максимальному значению критерия детерминации R2) описывающие дневную температуру в г. Томске в разные месяцы 1997-1999 гг.

Определить среднюю температуру месяца и отклонение от нее максимальной и минимальной температуры в процентах.

Вычислить коэффициент корреляции температуры для одних и тех же месяцев двух разных лет. Сделать выводы.

Коэффициент корреляции используется для определения наличия взаимосвязи между двумя различными рядами данных Xi , Yi , i = 1... n  и имеет вид:

.

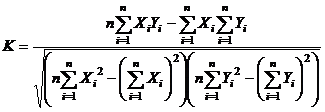О хорошей корреляции говорят значения К, по модулю близкие к единице. Знак «+» соответствует прямой взаимосвязи, знак «-» ― обратной. Вычисление этой формулы встроено в Excel (функция КОРРЕЛ).


Таблица 3.2 – Дневная температура в г. Томске в 1997–1999 гг. (по данным А.С. Минькова)

1997 г.

Месяц

День

Январь

Февраль

Март

Апрель

Май

Июнь

Июль

Август

Сентябрь

Октябрь

Ноябрь

Декабрь

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

–19

–17

–12

–3

–2

–15

–9

2

–18

–22

–25

–20

–13

–12

–20

–20

–5

–2

–3

–15

–20

–6

–4

–4

–14

–6

–11

–14

–10

–10

–4

–6

–15

–20

–12

–9

–8

–6

–12

–6

–6

–5

–4

–11

–7

–4

–1

0

–1

–2

–3

–11

–20

–16

–16

–16

–10

–6

–1

 

 

0

4

0

–4

–1

2

1

–1

–1

–1

–2

–3

0

2

–1

2

2

3

5

6

8

9

11

9

10

7

11

12

3

3

5

7

6

5

6

4

10

13

15

15

16

18

17

16

9

20

14

9

12

15

16

22

22

21

20

12

10

18

16

12

13

19

12

15

10

11

12

24

14

10

11

4

3

5

7

10

14

16

18

23

28

17

19

20

17

19

27

30

22

19

29

27

20

11

12

10

22

25

29

30

13

10

19

10

16

19

22

22

15

11

18

22

18

26

30

28

30

19

29

33

31

19

20

22

21

22

25

19

18

15

14

20

25

28

27

23

20

25

23

15

11

12

21

19

22

18

16

19

21

26

28

27

29

31

30

26

27

21

26

29

30

17

15

13

10

13

18

22

27

28

23

11

12

15

16

11

11

10

11

14

10

13

9

7

12

10

15

13

10

8

13

10

14

17

16

18

16

20

19

23

25

24

19

14

16

23

23

23

21

18

15

11

5

6

 

8

12

16

15

18

17

14

10

11

7

8

7

4

3

7

13

12

10

–3

–4

–3

2

4

5

5

–1

8

6

7

4

3

1

3

0

3

6

6

2

–4

–5

–5

–1

–14

–15

–7

–5

–2

–4

–21

–24

–15

–9

–25

–30

–23

–10

–15

–31

–30

–26

–17

 

–14

–9

–19

–28

–26

–9

–19

–22

–12

–17

–19

–13

–9

–22

–23

–25

–31

–20

–10

–11

–17

–9

–20

–29

–23

–12

–18

–15

–6

–19

–22

   Продолжение таблицы 3.2

1998 г.

Месяц

День

Январь

Февраль

Март

Апрель

Май

Июнь

Июль

Август

Сентябрь

Октябрь

Ноябрь

Декабрь

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

–32

–23

–13

–12

–13

–20

–20

–33

–30

–28

–27

–32

–29

–25

–27

–31

–24

–18

–16

–13

–19

–18

–15

–14

–15

–10

–12

–16

–13

–14

–17

–15

–12

–3

–10

–20

–14

–15

–16

–20

–29

–21

–10

–6

–3

1

–11

–16

–17

–12

–7

–5

–2

–10

–5

–4

–2

–4

–1

 

 

–6

–5

–3

–1

0

0

1

3

1

2

1

–1

1

–10

–15

–22

–1

0

1

0

1

3

5

2

–1

–2

–2

–8

–3

–4

0

6

4

5

–2

3

0

–3

1

1

3

5

0

–2

–1

0

2

–1

2

0

–2

0

–2

4

5

4

12

7

6

5

2

4

7

5

2

7

9

13

22

18

20

17

19

9

12

1

0

9

11

5

4

9

22

28

24

29

28

30

25

21

23

28

29

28

20

14

18

20

28

29

23

27

25

23

28

23

25

24

27

30

17

15

10

12

15

12

17

19

24

23

32

22

 

20

23

30

28

33

34

32

30

32

30

27

25

23

28

32

29

27

30

29

30

26

25

29

31

30

31

28

25

29

27

30

26

25

30

27

26

29

30

31

30

31

31

32

32

31

32

30

20

18

21

18

16

14

15

15

15

20

22

23

21

20

18

15

13

12

13

10

9

11

12

9

15

17

14

9

10

8

6

9

17

18

10

4

2

1

5

8

5

3

4

1

5

 

5

3

4

1

3

1

3

4

2

0

1

1

5

–2

–8

6

4

11

7

4

8

9

7

4

2

–1

4

–7

–10

–5

4

5

3

0

–7

–1

2

4

3

–1

7

–7

–12

–10

–15

–13

–12

–15

–9

–16

–17

–9

–17

–22

–20

–22

–25

–31

–34

–30

–23

–19

–22

–21

–16

–15

–4

–8

–13

–7

–9

–6

–10

–5

–2

–8

–10

–12

–5

–7

–6

–4

–3

–4

–1

–8

–20

–17

–13

–2

–5

0

 

Продолжение таблицы 3.2

1999 г.

Месяц

День

Январь

Февраль

Март

Апрель

Май

Июнь

Июль

Август

Сентябрь

Октябрь

Ноябрь

Декабрь

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

–4

–17

–25

–23

–25

–17

–14

–19

–14

–6

–12

–15

–17

–6

–9

–16

–20

–17

–8

–5

–8

–8

–31

–30

–36

–27

–21

–15

–9

–17

–18

–6

–8

–5

–2

2

–12

–9

–5

–2

0

3

0

–4

–4

–12

–16

–8

–11

–5

–6

–10

–7

–6

–3

–1

–7

–4

–2

 

–5

–10

–15

–23

–20

–22

–20

–15

–20

–13

–10

–13

–15

–13

–15

–10

–16

–13

–15

–5

–2

0

–11

–17

–12

–5

2

1

2

0

2

2

3

2

5

7

5

2

3

5

6

7

6

7

10

5

4

3

4

1

3

2

5

1

0

10

7

4

2

10

15

 

16

22

24

20

26

25

17

13

4

14

18

10

12

17

26

19

22

19

24

27

30

31

33

31

17

23

24

23

25

30

31

24

20

23

22

25

23

28

26

14

10

8

8

10

20

18

9

14

15

16

15

18

22

24

26

25

19

20

24

16

20

 

25

27

24

26

28

30

32

34

36

34

35

36

34

37

31

32

34

35

32

30

30

28

27

27

26

23

26

23

26

30

33

32

28

25

23

24

20

18

22

21

22

19

20

22

19

20

20

19

20

22

25

28

24

23

23

23

22

23

24

22

20

21

16

15

18

16

13

10

15

16

9

8

10

13

16

17

15

17

14

18

20

15

14

8

5

8

7

2

2

1

0

1

6

12

13

10

14

15

10

5

2

0

0

0

3

5

8

11

13

7

6

5

1

0

–1

–2

–2

–12

–6

–4

1

3

4

6

3

2

4

1

3

2

–2

–5

–7

–5

–13

–4

1

–2

–5

0

2

–8

–19

–25

–27

–25

–22

–19

–19

–17

–14

–12

–6

–7

–5

–4

–1

–6

–4

–5

–3

–13

–4

–2

–5

–4

–2

–1

–3

–12

–14

–17

–7

–1

–1

1

–5

–11

–10

–6

–19

–26

–36

–39

 

Лабораторная работа 4. Численное решение

уравнений

 

Задание 1. Нахождение корней полиномов при помощи табулирования и сервисной функции Подбор параметра.

Известно, что если функция, определенная в интервале [a,b], имеет значения F(а) и F(b) с разными знаками, то в интервале [a,b] есть, по крайней мере, один корень. Построить алгоритм нахождения корней уравнений с заданной точностью EPS следующим образом.

1. Определить начальный интервал [A, B], где находятся корни.

Для полиномов

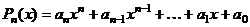
модули всех корней xk , k = 1…n расположены в круговом кольце

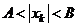,                                      (4.1)

где   .

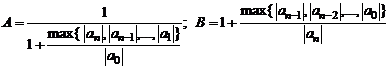Таким образом,  положительные  корни лежат в интервале [A, B], а отрицательные корни - в интервале [-B, -A].

2. Табулируя полином в найденных начальных интервалах (например, с шагом (В-А)/10), составить таблицу {x, P(x)}.

3. Определить две соседние ячейки х, где функция меняет свой знак. Одно из значений (для которого значение функции ближе к нулю) принять за начальное приближение к корню полинома.

4. Уточнение корня производится методом последовательных приближений с помощью сервисной команды Подбор параметра (меню Сервис). Относительная погрешность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры (Сервис з Параметры з Вычисления) (рис. 4.1).

5. Открыть  диалоговое окно  Подбор параметра  (рис. 4.2). В поле Установить в ячейке ввести адрес ячейки, где вычисляется значение полинома. В поле Значение ввести 0 (т.е. искомое значение полинома). В поле Изменяя значение ячейки ввести адрес ячейки, отведенной для переменной х, где должно находиться начальное приближение к корню полинома.

 


Примечание. В этой ячейке должно содержаться числовое значение, а не формула, его вычисляющая. Для того, чтобы заменить в ячейке формулу на ее числовое значение, необходимо, находясь в этой ячейке, вызвать контекстно-зависимое меню и выбрать Копировать. Затем, находясь в той же ячейке, снова вызвать контекстно-зависимое меню и выбрать Специальная вставка (рис. 4.3).

В появившемся диалоговом окне отметить Значения. После этого ячейка готова к использованию в поле Изменяя значение ячейки диалогового окна Подбор параметра.

6. После подбора параметра (ОК) х получит значение корня. Процесс повторяется для всех найденных начальных приближений в диапазоне, определяемом формулой (4.1).

 

 

 

 


Данные для решения взять из таблицы 4.1. Корни найти с точностью EPS=0,00001.

 

Таблица 4.1 - Полиномы

Вариант

Уравнение

Вариант

Уравнение

1

x4+6x3+11x2–2x–28=0

16

x4+3x3+8x2–5=0

2

x4+5x3+9x2+5x–1=0

17

x4–6x3+11x2+2x–28=0

3

x4+3x3+3x2–2=0

18

x4–5x3+9x2–5x–1=0

4

x4+x3–7x2+8x–6=0

19

x4–3x3+3x2–2=0

5

x4–10x3+16x+5=0

20

x4–x3–7x2–8x–6=0

6

x4–3x3–4x2–x–3=0

21

x4–10x2–16x+5=0

7

x4+4x3+4x2+4x–1=0

22

x4+3x3+4x2+x–3=0

8

x4+6x3+13x2+10x+1=0

23

x4–4x3–4x2–4x–1=0

9

x4+x3–4x2+16x–8=0

24

x4+2x3+3x2+2x–2=0

10

x4–x3–4x2–11x–3=0

25

x4–6x3+13x2–10x+1=0

11

x4–6x3–12x–8=0

26

x4–3x2+4x–3=0

12

x4+4x3+4x2–4=0

27

x4–6x2+12x–8=0

13

x4+x3+2x+1=0

28

x4–4x3+4x2–4=0

14

x4+2x3+x2+2x+1=0

29

x4–x3–2x+1=0

15

x4+3x2–4x–1=0

30

x4–2x3+x2–2x+1=0

 

Задание 2. Нахождение корней нелинейных уравнений с помощью метода итераций.

Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций уравнение представляют в виде x=F(x) и записывают итерационную схему

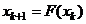,                                               (4.2)

с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, которое выбирается самостоятельно. Достаточное условие сходимости процесса: в окрестности корня  | F /(x)| <1.

Порядок действий в Excel может быть следующий.

1.       Представить данное уравнение в виде x=F(x).

2.       Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.

3.       В первую ячейку первой строки таблицы занести значение 0, во вторую – начальное приближение.

4.       В следующие строки занести, соответственно, номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5).

5.       Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения EPS.

Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x).

В этом может оказать помощь другой итерационный метод решения нелинейных уравнений – метод Ньютона. Его итерационная схема имеет вид

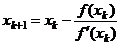                          .                            (4.3)

Сравнивая (4.2) и (4.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (4.3). В большинстве случаев метод Ньютона сходится быстрее.

Данные для решения взять из таблицы 4.2. Точность решения EPS=0,0001.

После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат – очередное приближение к корню.

 

Задание 3. Нахождение корней нелинейных уравнений методом бисекции.

Если метод итераций сходится не всегда, то метод бисекции (или метод деления отрезка пополам, или метод дихотомии) – безусловно сходящийся метод нахождения корней нелинейного уравнения F(x)=0, лишь бы был известен отрезок, на котором расположен корень уравнения.

Пусть непрерывная функция F(x) меняет знак на концах отрезка [a,b], т.е. F(a)ЧF(b) < 0. Назовем такой отрезок отрезком локализации корня: на нем есть, по крайней мере, один корень. Найдем координату середины этого отрезка c=(a+b)/2 и рассмотрим два получившихся отрезка [a,c] и [c,b]. Если F(a)ЧF(с) < 0, то корень находится на отрезке [a,c], в противном случае – на отрезке [с,b]. Процесс деления все новых и новых отрезков локализации корня продолжаем до тех пор, пока длина отрезка не станет меньше заданной величины точности решения EPS.

 

Таблица 4.2 – Нелинейные уравнения

Вариант

Уравнение

Вариант

Уравнение

1

ln(x)+(x+1)3=0

16

x–sin(x)=0,25

2

xЧ2x=1

17

tg(0,58x+0,1)=x2

3

Ö x+1 = 1/x

18

Ö x– cos(0,387x)=0

4

x–cos(x)=0

19

3x–cos(x)–1=0

5

3x+cos(x)+1=0

20

lg(x)–7/(2x+6)=0

6

x+ln(x)=0,5

21

x+lg(x)=0,5

7

2–x=ln(x)

22

x2+4sin(x)=0

8

(x–1)2=exp(x)/2

23

ctg(1,05x)–x2=0

9

(2–x)exp(x)=0,5

24

xЧlg(x)–1,2=0

10

2,2x–2x=0

25

ctg(x)–x/4=0

11

x2+4sin(x)=0

26

2x–lg(x)–7=0

12

2x–lg(x)=7

27

2arctg(x)-1/(2x3)=0

13

5x–8Чln(x)=8

28

2cos(x+p/6)+x2=3x–2

14

sin(x-0,5)–x+0,8=0

29

cos(x+0,3)=x2

15

2Чlg(x)–x/2+1=0

30

x2cos(2x)=–1

При использовании Excel достаточно внести в некоторые ячейки, лежащие в одной строке, формулы, осуществляющие:

-      вычисление значений левой и правой границы отрезков локализации;

-      нахождение середины отрезка;

-      вычисление произведения значений функций в левой и правой границах отрезка (для контроля правильности алгоритма);

-      проверку на точность решения (аналогично предыдущему заданию).

Затем формулы копируются вниз по столбцам до тех пор, пока не будет найден корень с заданной степенью точности EPS=0,0001.

Данные для решения взять из таблицы 4.2, то есть решить одно и то же уравнение двумя способами.

 

Задание 4. Решение систем линейных алгебраических уравнений.

В Excel имеются специальные функции для работы с матрицами (Вставка функции пМатематические):

МОБР           вычисление обратной матрицы А-1;

МОПРЕД       вычисление определителя матрицы D;

МУМНОЖ      нахождение произведения двух матриц.

С их помощью можно решать системы линейных алгебраических уравнений вида

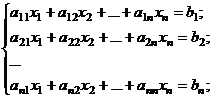                 (4.4)

или в матричном виде

АЧХ=В,

где А = {aij}– матрица коэффициентов при неизвестных; В = {bij} – вектор-столбец правых частей уравнений; Х = {xij} – вектор-столбец неизвестных.

Способ 1 (метод обратной матрицы).  Решение имеет вид Х = А–1ЧВ, где А–1 – матрица, обратная по отношению к матрице А.

С помощью функции МОБР находится обратная матрица, а затем с помощью функции МУМНОЖ она перемножается с вектором-столбцом правых частей уравнений.

Примечание. При работе с матрицами перед вводом формулы необходимо выделить область на рабочем листе, куда будет выведен результат вычисления, а после задания исходных данных в поле функции выйти не как обычно, нажатием клавиши Enter или кнопки ОК,  а нажатием клавиш Ctrl + Shift + Enter.

Способ 2 (правило Крамера). Если определитель D, составленный из коэффициентов при неизвестных, отличен от нуля, то решение имеет вид

x j = Dj / D ,  j=1...n.                           (4.5)

Здесь Dj – дополнительный определитель, полученный из главного определителя системы D путем замены его j-го столбца  вектором-столбцом В.

С помощью функции МОПРЕД находятся главный и дополнительные определители, и по формулам (4.5) вычисляются корни СЛАУ.

Способ 3 (метод исключений Гаусса). Этот метод основан на приведении  матрицы  системы  к треугольному виду,  что достигается последовательным  исключением  неизвестных из уравнений  системы.

Предположим, что в (4.4) a11 ¹ 0. Разделим первое уравнение системы на a11 (этот коэффициент называется ведущим или главным элементом), получим

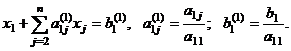
Затем из каждого из остальных уравнений вычитается первое уравнение, умноженное на соответствующий коэффициент ai1 (i=2,3,¼, n).

Эти n–1 уравнений принимают вид

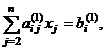
где      

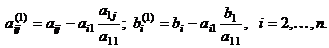
Далее аналогичную процедуру выполняют с этой системой, оставляя в покое первое уравнение. Только теперь делят на другой ведущий элемент a22(1) ¹0.

В результате исключения неизвестных приходим к СЛАУ с верхней треугольной матрицей с единицами на главной диагонали:

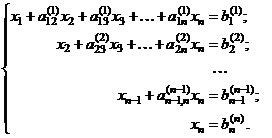                 (4.6)

 

Индексы над коэффициентами означают, сколько раз  данное уравнение преобразовывалось.

Прямой ход метода Гаусса завершен.

Обратный ход метода Гаусса заключается в нахождении неизвестных xn, xn-1, ... , x1 , причем в указанном порядке.

В этом списке xn уже определено из последнего уравнения системы (4.6), а общая формула обратного хода имеет вид:

 

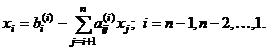
Проиллюстрируем этот алгоритм на примере решения системы из трех уравнений.

1. Располагаем на листе Excel матрицу коэффициентов и столбец правых частей (т.н. расширенная матрица 3´4), например, в ячейках А4:D6 (рис. 4.4).

2. Выделяем диапазон ячеек А8:D8 и вводим формулу:

{=A4:D4/A4}.

Фигурные скобки появляются автоматически при вводе формулы комбинацией клавиш Shift+Ctrl+Enter, как признак того, что идет работа не с отдельными ячейками, а с массивами.

3. Выделяем диапазон ячеек А9:D9, вводим формулу

{=A5:D5-$A$8:$D$8*B5}

и копируем эту формулу в диапазон ячеек А10:D10. В ячейках А9 и А10 появились нули.

4. В ячейки А12:D12 копируем значения первой строки расширенной матрицы А8:D8, в ячейки А13:D13 – формулу

{=A9:D9/B9}.

При этом второй элемент главной диагонали матрицы коэффициентов становится равным единице.

 


В ячейки А14:D14 вводим формулу

{=A10:D10–$A$13:$D$13*B10}.

5) В ячейки А16:D17 копируем значения первых двух строк расширенной матрицы (А12:D13), а в ячейки А18:D18 – формулу

{=A14:D14/C14}.

Прямой ход метода Гаусса завершен: получилась верхняя треугольная матрица с диагональными элементами, равными 1.

 

Решить тремя способами систему линейных алгебраических уравнений, взяв данные для решения из таблицы 4.3.

Проверить найденное решение умножением матрицы коэффициентов на вектор-столбец решения.

 

 

 

 

 

 

Таблица 4.3 – Системы линейных алгебраических уравнений

Вариант

СЛАУ

Вариант

СЛАУ

1

2,7x1+3,3x2+1,3x3=2,1;

3,5x1–1,7x2+2,8x3=1,7;

4,1x1+5,8x2–1,7x3=0,8

2

0,34x1+0,71x2+0,63x3=2,08;

0,71x1–0,65x2–0,18x3=0,17;

1,17x1–2,35x2+0,75x3=1,28

 

3

1,7x1+2,8x2+1,9x3=0,7;

2,1x1+3,4x2+1,8x3=1,1;

4,2x1–3,3x2+1,3x3=2,1

4

3,75x1–0,28x2+0,17x3=0,75;

2,11x1–0,11x2–0,12x3=1,11;

0,22x1–3,17x2+1,81x3=0,05

 

5

3,1x1+2,8x2+1,9x3=0,2;

1,9x1+3,1x2+2,1x3=2,1;

7,5x1+3,8x2+4,8x3=5,6

 

6

0,21x1–0,18x2+0,75x3=0,11;

0,13x1+0,75x2–0,11x3=2,00;

3,01x1–0,33x2+0,11x3=0,13

 

7

9,1x1+5,6x2+7,8x3=9,8;

3,8x1+5,1x2+2,8x3=6,7;

4,1x1+5,7x2+1,2x3=5,8

 

8

0,13x1–0,14x2–2,00x3=0,15;

0,75x1+0,18x2–0,77x3=0,11;

0,28x1–0,17x2+0,39x3=0,12

 

9

3,3x1+2,1x2+2,8x3=0,8;

4,1x1+3,7x2+4,8x3=5,7;

2,7x1+1,8x2+1,1x3=3,3

 

10

3,01x1–0,14x2–0,15x3=1,00;

1,11x1+0,13x2–0,75x3=0,13;

0,17x1–2,11x2+0,71x3=0,17

 

11

7,6x1+5,8x2+4,7x3=10,1;

3,8x1+4,1x2+2,7x3=9,7;

2,9x1+2,1x2+3,8x3=7,8

 

12

0,92x1–0,83x2+0,62x3=2,15;

0,24x1–0,54x2+0,43x3=0,62;

0,73x1–0,81x2–0,67x3=0,88

 

13

3,2x1–2,5x2+3,7x3=6,5;

0,5x1+0,34x2+1,7x3=-0,2

1,6x1+2,3x2–1,5x3=4,3

 

14

1,24x1–0,87x2–3,17x3=0,46;

2,11x1–0,45x2+1,44x3=1,50;

0,48x1+1,25x2–0,63x3=0,35

 

15

5,4x1–2,3x2+3,4x3=-3;

4,2x1+1,7x2–2,3x3=2,7;

3,4x1+2,4x2+7,4x3=1,9

 

16

0,64x1–0,83x2+4,2x3=2,23;

0,58x1–0,83x2+1,43x3=1,71;

0,86x1+0,77x2+0,88x3=–0,54

 

17

3,6x1+1,8x2–4,7x3=3,8;

2,7x1–3,6x2+1,9x3=0,4;

1,5x1+4,5x2+3,3x3=-1,6

 

18

0,32x1–0,42x2+0,85x3=1,32;

0,63x1–1,43x2–0,58x3=-0,44;

0,84x1–2,23x2–0,52x3=0,64

 

 

 

Продолжение таблицы 4.3

Вариант

СЛАУ

Вариант

СЛАУ

19

5,6x1+2,7x2–1,7x3=1,9;

3,4x1–3,6x2–6,7x3=-2,4;

0,8x1+1,3x2+3,7x3=1,2

 

20

0,73x1+1,24x2–0,38x3=0,58;

1,25x1+0,66x2–0,78x3=0,66;

0,75x1+1,22x2–0,83x3=0,92

 

21

2,7x1+0,9x2–1,5x3=3,5;

4,5x1–2,8x2+6,7x3=2,6;

5,1x1+3,7x2–1,4x3=-0,14

 

22

0,62x1–0,44x2–0,86x3=0,68;

0,83x1+0,42x2–0,56x3=1,24;

0,58x1–0,37x2–0,62x3=0,87

 

23

4,5x1–3,5x2+7,4x3=2,5;

3,1x1–0,6x2–2,3x3=-1,5;

0,8x1+7,4x2–0,5x3=6,4

 

24

1,26x1–2,34x2+1,17x3=3,14;

0,75x1+1,24x2–0,48x3=–1,17;

3,44x1–1,85x2+1,16x3=1,83

 

25

3,8x1+6,7x2–1,2х3=5,2;

6,4x1+1,3x2–2,7x3=3,8;

2,4x1–4,5x2+3,5x3=–0,6

 

26

0,46x1+1,72x2+2,53x3=2,44;

1,53x1–2,32x2–1,83x3=2,83;

0,75x1+0,86x2+3,72x3=1,06

 

27

5,4x1–6,2x2–0,5x3=0,52;

3,4x1+2,3x2+0,8x3=-0,8;

2,4x1–1,1x2+3,8x3=1,8

 

28

2,47x1+0,65x2–1,88x3=1,24;

1,34x1+1,17x2+2,54x3=2,35;

0,86x1–1,73x2–1,08x3=3,15

 

29

7,8x1+5,3x2+4,8x3=1,8;

3,3x1+1,1x2+1,8x3=2,3;

4,5x1+3,3x2+2,8x3=3,4

 

30

4,24x1+2,73x2–1,55x3=1,87;

2,34x1+1,27x2+3,15x3=2,16;

3,05x1–1,05x2–0,63x3=–1,25

 

31

3,8x1+4,1x2–2,3x3=4,8;

2,1x1+3,9x2–5,8x3 = 3,3;

1,8x1+1,1x2–2,1x3=5,8

 

32

0,43x1+1,24x2–0,58x3=2,71;

0,74x1+0,83x2+1,17x3=1,26;

1,43x1 - 1,58x2+0,83x3=1,03

 

33

1,7x1–2,2x2+3,0x3=1,8;

2,1x1+1,9x2–2,3x3=2,8;

4,2x1+3,9x2–3,1x3=5,1

 

34

0,43x1+0,63x2+1,44x3=2,18;

1,64x1–0,83x2–2,45x3=1,84;

0,58x1+1,55x2+3,18x3=0,74

 

35

2,8x1+3,8x2–3,2x3=4,5;

2,5x1–2,8x2+3,3x3=7,1;

6,5x1–7,1x2+4,8x3=6,3

 

36

1,24x1+0,62x2–0,95x3=1,43;

2,15x1–1,18x2+0,57x3=2,43;

1,72x1–0,83x2+1,57x3=3,88

 

 

 

Продолжение таблицы 4.3

Вариант

СЛАУ

Вариант

СЛАУ

37

3,3x1+3,7x2+4,2x3=5,8;

2,7x1+2,3x2–2,9x3=6,1;

4,1x1+4,8x2–5,0x3=7,0

 

38

0,62x1+0,56х2–0,43x3=1,16;

1,32x1–0,88x2+1,76x3=2,07;

0,73x1+1,42x2–0,34x3=2,18

 

39

7,1x1+6,8x2+6,1x3=7,0;

5,0x1+4,8x2+5,3x3=6,1;

8,2x1+7,8x2+7,1x3=5,8

 

40

1,06x1+0,34x2+1,26x3=1,17;

2,54x1–1,16x2+0,55x3=2,23;

1,34x1–0,47x2–0,83x3=3,26

 

 

Задание 5. Решение систем нелинейных уравнений.

С помощью сервисной программы Поиск решения (Сервис | Поиск  решения)  в Excel можно решать системы нелинейных уравнений.

В общем случае система нелинейных уравнений имеет вид:

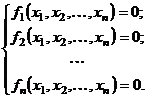                                                (4.7)

Составим новую функцию F(x1, х2, ..., хn), представляющую собой сумму квадратов правых частей уравнений:

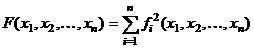.                    (4.8)

Очевидно, переменные x1, х2, ..., хn , являющиеся решением системы (4.7), с необходимостью и достаточностью являются также решением уравнения

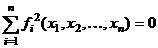.                                            (4.9)

Путь решения следующий.

На листе Excel отводим ячейки для неизвестных данной системы уравнений, например с А1 по А5 (если пять переменных), и вводим туда начальные приближения. В ячейку В2 вводим формулу, вычисляющую функцию (4.8).

Открываем диалоговое окно Поиск решения (рис. 4.5). В поле Установить целевую ячейку вводим В2, в группе Равной устанавливаем переключатель в положение Значению и в поле ввода задаем 0. В поле Изменяя ячейки вводим диапазон ячеек А1:А5.


После нажатия на кнопку Выполнить будет найдено решение, которое поместится в ячейки А1:А5. В ячейке В2 будет вычислено значение левой части уравнения (4.9) с относительной погрешностью, задаваемой в диалоговом окне Параметры поиска решения .

Примечание 1. При неудачном выборе вектора начального приближения решение может быть не найдено. Поэтому необходим предварительный анализ системы уравнений с целью определения лучшего (более близкого к корню) начального приближения. Например, для системы из двух уравнений можно затабулировать функцию (4.8) и в качестве начальных выбрать приближения, наиболее близкие к нулю.

Примечание 2. Система уравнений может иметь несколько корней, поэтому необходим ее анализ и с этой стороны. Задавая разные начальные приближения, можно получить разные решения системы.

Примечание 3. Более подробно о возможностях программы Поиск решения изложено в лабораторной работе 12.

 

Решить систему нелинейных уравнений, взяв данные из таблицы 4.4. Проверить найденное решение.

Таблица 4.4 – Системы нелинейных уравнений

Вариант

СНУ

Вариант

СНУ

1

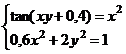
2

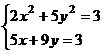
3

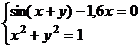
4

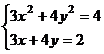
5

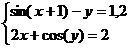
6

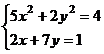
7

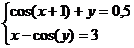
8

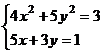
9

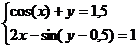
10

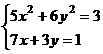
11

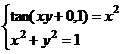
12

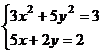
13

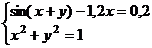
14

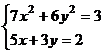
15

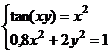
16

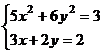
17

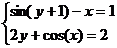
18

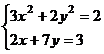
19

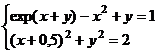
20

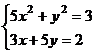
21

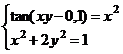
22

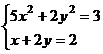
Продолжение таблицы 4.4

Вариант

СНУ

Вариант

СНУ

23

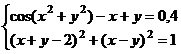
24

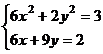
25

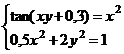
26

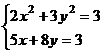
27

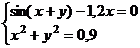
28

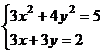
29

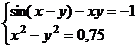
30

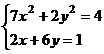
31

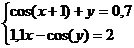
32

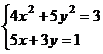
33

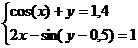
34

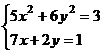
35

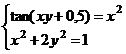
36

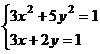
37

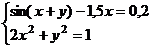
38

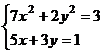
39

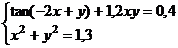
40

 

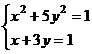
Построить поверхность, описываемую функцией F(x, y) в окрестности одного из корней, пользуясь описанием, приведенным в лабораторной работе 2.

 

 

Лабораторная работа 5. Электронная таблица как база данных. Сортировка и фильтрация данных

 

Область электронной таблицы можно рассматривать как базу данных. При этом столбцы называются полями, а строки – записями. Столбцам присваиваются имена, которые будут использоваться как имена полей записей.

Существует ряд ограничений, накладываемых на структуру базы данных:

-      первый ряд базы данных должен содержать неповторяющиеся имена полей и располагаться в одной строке;

-      для имен полей следует использовать шрифт, тип данных, формат, рамку, отличные от тех, которые используются для данных в записях;

-      таблицу следует отделить от других данных рабочего листа пустым столбцом и пустой строкой;

-      информация по полям должна быть однородной, т.е. только цифры или только текст.

Работа с любой базой данных заключается в поиске информации по определенным критериям, перегруппировке и обработке информации.

 

Задание 1. Привести все данные в исходной таблице 5.1 к параметрам Земли, используя только абсолютную адресацию (не забудьте сменить размерность величин в заголовках новой таблицы!).

В полученной таблице, используя Данные | Сортировка или «горячие клавиши» Сортировка по возрастанию и Сортировка по убыванию:

1) отсортировать данные в порядке убывания количества спутников;

2) отсортировать данные в алфавитном порядке названий планет;

3) отсортировать данные в порядке возрастания массы.

Разместить результаты сортировки (а затем и результаты фильтрации) на различных листах рабочей книги.

 

 

 

 

Таблица 5.1 – Планеты Солнечной системы

Планета

Период

обращения, земной год

Расстояние от Солнца,

 млн. км

Диаметр,

тыс. км

Масса,

Тт

Количество спутников

Меркурий

0,241

58

4,9

0,32×109

0

Венера

0,615

108

12,1

4,86×109

0

Земля

1

150

12,8

6,0×109

1

Марс

1,881

288

6,8

6,1×108

2

Юпитер

11,86

778

142,6

19,07×1011

16

Сатурн

29,46

1426

120,2

57,09×1010

17

Уран

84,01

2869

49,0

87,24×109

14

Нептун

164,8

4496

50,2

10,34×1010

2

Плутон

247,7

5900

2,8

0,1×109

1

 

Задание 2.  С помощью Автофильтра осуществить:

1)    поиск планет, имеющих диаметр менее 4-х диаметров Земли и массу менее массы Земли;

2)    поиск планет, находящихся от Солнца на расстоянии не менее 0,5 расстояния от Земли, имеющих массу от одной до 100 масс Земли и не более 2-х спутников;

3)    поиск трех планет, имеющих самый большой диаметр.

Вызов Автофильтра происходит при выполнении последовательности действий Данные | Фильтр | Автофильтр. При этом в ячейках, где располагаются заголовки, появляются кнопки. При нажатии на них появляется меню с условиями отбора автофильтра.

Все – задает все строки.

Первые 10 – определяет строки с максимальным или минимальным значением ячеек текущего столбца. Эта строка открывает диалоговое окно Наложение условия по списку (рис. 5.1).


Условие – выбирает строки, удовлетворяющие одному или двум условиям. Эта строка меню открывает диалоговое окно Пользовательский автофильтр (рис. 5.2), где в левом поле под надписью Показать только те строки, значения которых, выбирается необходимый оператор сравнения (равно, меньше, больше и т.п.), а в правом поле задается значение сравнения. Нижние поля используются для второго условия отбора, соединяющегося с первым знаками логических операций И или ИЛИ.


Задание 3. С помощью Расширенного фильтра осуществить поиск планет с периодом обращения более 10 земных лет и количеством спутников не менее 2-х.

Для этого следует сначала определить (создать) три области (диапазона):

1)       исходный диапазон - область базы данных;

2)       диапазон условий - область, где задаются критерии фильтрации;

3)       диапазон результатов - область, в которой будут появляться результаты фильтрации.

Первый диапазон уже определен – это преобразованная исходная таблица (пусть, например, она располагается в ячейках А1:F10). Второй диапазон (пусть это будет А12:F13) необходимо сформировать из строки заголовков таблицы (просто скопировав ее; отметим, что эта строка не должна являться результатом объединения нескольких ячеек!) и строки, где в соответствующих ячейках записываются условия фильтрации (например, >10, >=2 и т.п.). Третий диапазон нужен, если результат фильтрации собираются расположить не на месте исходного диапазона, а в другом месте. Он также состоит из строки заголовков и нескольких пустых строк (например, А15:F17). В эти строки запишется результат фильтрации. Если отведенных строк не хватит, появится предупредительное сообщение, и фильтрация может быть продолжена.

Чтобы выполнить фильтрацию, необходимо воспользоваться командами  меню  Данные | Фильтр | Расширенный фильтр  (рис. 5.3)  и  в открывшемся  диалоговом  окне  указать  ячейки диапазонов.


Опция  Только  уникальные  записи позволяет исключить из таблицы все повторяющиеся строки, оставив только уникальные. Для этого необходимо ее пометить и провести фильтрацию, не задавая диапазон условий.

Чтобы восстановить таблицу после работы Автофильтра или Расширенного фильтра, следует выполнить следующие действия: Данные | Фильтр | Отобразить все.

 

 

 

Лабораторная работа 6. Сводные таблицы

 

Сводная таблица – это еще один инструмент Excel для обработки больших списков с данными.


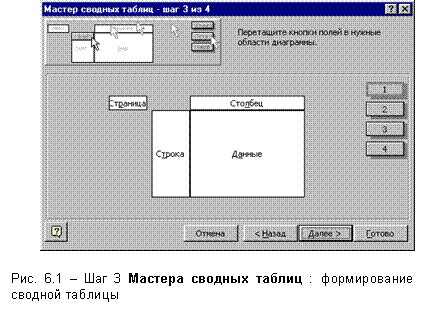
Сводная таблица обслуживается Мастером сводных таблиц (Данные | Сводная таблица ), позволяющим сразу подводить итоги, выполнять сортировку и фильтрацию списков. Построение сводной таблицы осуществляется за четыре шага. На первом шаге указывается источник данных, на втором шаге – диапазон ячеек, где находятся данные. Третий шаг – самый основной. Здесь формируется требуемый вид сводной таблицы, исходя из условия поставленной задачи (рис. 6.1).

Это осуществляется путем перетаскивания кнопок с названиями полей, которые располагаются в правой части, в области Строка, Столбец, Данные, Страница. Затем двойным щелчком по перенесенной кнопке можно изменить параметры каждой области.

На  четвертом шаге указывается, где поместить сводную таблицу.

 

 

Задание 1. Заполнить таблицу 6.1, занеся недостающие данные, рассчитав процент удержания по следующему правилу: при количестве иждивенцев более трех – 0%, при трех – 5%, при двух – 10%, при одном – 12%, если нет – 14%. Расчет оформить с помощью вложенных функций ЕСЛИ.

 

Задание 2. Построить сводную таблицу, найдя суммы по полям Всего начислено, Всего удержано, Сумма к выдаче по каждой фамилии, расположив фамилии в алфавитном порядке и проклассифицировав отдельно по категории Количество иждивенцев. Поместить сводную таблицу на отдельном листе. Постарайтесь создать компактную и наглядную сводную таблицу, избежав излишнего текста и пустых ячеек.

 

Таблица 6.1 – Ведомость

Ф.И.О.

Отдел

Количество иждивенцев

Всего начислено, руб.

% удержания

Всего удержано, руб.

Сумма к выдаче, руб.

1. Петухова К.И.

1

1

1260

 

 

 

2. Безенчук П.Ф.

3

2

1100

 

 

 

3. Воробьянинов И.М.

2

3

800

 

 

 

4. Востриков Ф.О.

2

2

750

 

 

 

5. Коробейников В.А.

3

1

715

 

 

 

6. Грицацуева В. С.

1

3

630

 

 

 

7. Гаврилин З.С.

1

4

620

 

 

 

8. Треухов Т.И.

3

1

560

 

 

 

9. Изнуренков А.В.

1

0

420

 

 

 

10. Щукина Э.Е.

3

1

250

 

 

 

 

 

Задание 3. Построить новую сводную таблицу, разбив персонал по отделам и по категории Количество иждивенцев, и определить итоговую сумму к выдаче внутри каждого отдела. При выполнении этого задания рекомендуется использовать область Страница для размещения в нем поля Отдел.

 

 

Лабораторная работа 7. Консолидация данных (связь таблиц)

 

Excel позволяет связывать ячейки электронных таблиц, находящихся на различных рабочих листах одного файла, в разных файлах, на различных логических дисках таким образом, чтобы в результате ввода значений в одну таблицу изменялось бы содержание другой.

Связь данных можно осуществлять различными способами.

 

Способ 1. Формула связи. Связь между листами можно задать путем введения в один лист формулы связи со ссылкой на ячейку в другом листе =НазвЛиста!АдрЯч  (восклицательный знак обязателен).

Связь между файлами можно задать путем введения в один файл формулы связи со ссылкой  на ячейку в другом файле, указав полный путь к этому файлу, например, ='A:\Папка\[ИмяФайла.xls] НазвЛиста'!АдрЯч . Путь заключен в одинарные кавычки, имя файла заключено в квадратные скобки.

Используя формулы связи, можно в ячейках итоговой таблицы совершать любые операции над ячейками исходных таблиц.

 

Способ 2. Консолидация данных. Консолидация позволяет объединять данные из областей-источников и выводить их в области назначения. При этом могут использоваться различные функции: суммирования, расчета среднего арифметического, подсчетов минимальных и максимальных значений и т.п.

Для проведения консолидации необходимо, создав итоговую таблицу, выбрать Данные | Консолидация (рис. 7.1) и в поле Ссылка определить по порядку области-источники, данные из которых нужно консолидировать, добавляя их в поле Список диапазонов. Не забудьте поставить флажок напротив опции Создавать связи с исходными данными!

 

Задания

Задание 1. Заполните таблицу 7.1, создав ее на листе Январь.

 

 

 

 

 


Таблица 7.1 – Торговая фирма «Шмидт и сыновья»

Исходные данные за январь

Наименование продукции

Цена в У.Е.

Продано

Выручка

Телевизоры

350

20

 

Видеомагнитофоны

320

65

 

Музыкальные центры

750

15

 

Видеокамеры

970

30

 

Видеоплейеры

200

58

 

Аудиоплейеры

40

18

 

Радиотелефоны

390

11

 

Итого

 

 

 

 

Скопируйте таблицу на два других листа, назвав их Февраль и Март. Измените данные второго и третьего столбца (по вашему усмотрению).

На четвертом листе (Квартал. Способ 1) создайте макет таблицы сводных показателей (Продано и Выручка за квартал). Заполните эту таблицу, суммируя данные, находящиеся в  соответствующих ячейках листов показателей за январь - март.

На пятом листе (Квартал. Способ 2) получите аналогичную таблицу, но с помощью консолидации.

Изучите структуру полученной консолидированной таблицы. Она содержит скрытые строки, в которых находится информация из других листов. Скрытые строки можно открывать и снова скрывать, нажимая соответственно кнопки «+» и «–». Проверьте, изменяются ли значения консолидированной таблицы при изменениях в исходных таблицах.

Сравните оба способа.

 

Задание 2. Выбрав данные из таблицы 7.2, разнести их поквартально по разным листам одного файла. Определить среднюю цену  производителей  по каждой позиции в каждом квартале (в тыс. руб.) и соотношение цен на отдельные виды энергоресурсов с ценой на нефть (в процентах). В другом файле с помощью консолидации сформировать таблицу Среднегодовые цены. Для переноса текстовой информации (имена строк и столбцов) используйте опцию Использовать в качестве имен.

 

Таблица 7.2 – Цены производителей на отдельные виды энергоресурсов*)

Период

Цены, тыс. руб. за тонну

Нефть

Бензин автомобильный

Топливо дизельное

Мазут

топочный

Газ

естественный**)

Уголь

энергетический

для коксования

1997 г.

апрель

май

июнь

июль

август

сентябрь

октябрь

ноябрь

декабрь

 

1998 г.

январь

февраль

март

 

370

373

376

371

372

375

375

375

376

 

 

384

379

353

 

933

886

907

932

949

968

968

978

1011

 

 

1007

1001

1054

 

943

944

947

970

980

984

981

981

1013

 

 

1012

1011

985

 

443

433

434

440

437

436

441

440

440

 

 

440

445

438

 

37,2

39,0

39,0

39,0

39,3

39,3

39,5

39,6

39,4

 

 

40,2

40,3

44,6

 

144

143

146

141

141

141

139

137

138

 

 

140

148

146

 

133

130

138

129

136

129

127

128

124

 

 

125

122

123

*)Цены приведены на энергоресурсы, отгруженные на внутрироссийский рынок

**)За тысячу кубических метров

 

 

Лабораторная  работа  8.  Составление штатного расписания больницы. Создание простых макросов

 

Вы - заведующий больницей. Составьте штатное расписание, то есть определите, сколько сотрудников, на каких должностях и с каким окладом вы должны принять на работу. Общий месячный фонд зарплаты составляет $10.000.

Предположим, что для нормальной работы больницы нужно 5-7 санитарок, 8-10 медсестер, 10-12 врачей, 1 заведующий аптекой, 3 заведующих отделениями, 1 главный врач, 1 заведующий хозяйством, 1 заведующий больницей.

Предлагается следующая модель решения задачи. За основу берется оклад санитарки, а остальные вычисляются исходя из него с помощью коэффициентов оклада:

Оклад = А * (Оклад санитарки) + В.

Коэффициенты назначаются следующим образом:

медсестра должна получать в 1,5 раза больше санитарки;

врач - в 3 раза больше санитарки;

заведующий отделением - на $30 больше, чем врач;

заведующий аптекой - в 2 раза больше санитарки;

заведующий хозяйством - на $40 больше медсестры;

главный врач - в 4 раза больше санитарки;

заведующий больницей - на $20 больше главного врача.

 

Задание

1. Оформите таблицу, используя следующие столбцы: Должность, Количество сотрудников, Коэффициенты оклада (два столбца), Оклад, Итого.

При решении задачи используйте сервисную функцию Excel «Подбор параметра»: Сервис | Подбор параметра (рис. 8.1). 

В поле Установить в ячейке ввести адрес ячейки, где вычисляется  общая месячная зарплата всех сотрудников больницы. В поле Значение ввести предельное значение месячного фонда зарплаты. В поле Изменяя значение ячейки ввести адрес ячейки, где находится оклад санитарки. После нажатия ОК произойдет автоматический подбор значения оклада санитарки таким образом, чтобы общий месячный фонд зарплаты составил $10.000.

 

 


2. Рассчитайте оклады для нескольких вариантов штата, изменяя количество штатных единиц в соответствии с заданными условиями.

Для этого несколько раз подряд придется выполнять рутинные действия по вызову команды «Подбор параметра» и заполнению всех полей ее диалогового окна.

Для упрощения этой работы создадим простейший макрос – программу на языке VBA (Visual Basic for Application), встроенном в офисные программы. Причем сделаем это, не зная пока самого языка. В этом нам поможет MacroRecorder – транслятор, переводящий на язык VBA действия пользователя с момента запуска MacroRecorder до окончания записи макроса.


Для активизации MacroRecorder выбираем команду Сервис | Макрос | Начать запись. В появившемся диалоговом окне Запись макроса (рис. 8.2) задаем имя макроса («Staff») и описание макроса (не обязательно). В поле Сохранить в: оставляем опцию по умолчанию Эта книга (тогда созданный макрос сохранится на новом листе модуля в активной рабочей книге).

После нажатия ОК на экране появляется плавающая панель с кнопкой Остановить запись. Теперь все ваши действия над ячейками будут записываться.

В данном случае действия будут простые. Вызовем сервисную функцию Подбор параметра, выполним описанные ранее действия по расчету штатного расписания и остановим запись макроса.

Чтобы посмотреть, какая же все-таки VBA - программа «создана» нами, выполним команду  Сервис  |  Макрос  |  Макросы |.  В появившемся диалоговом окне выберем макрос с именем «Staff» и нажмем кнопку Изменить. Откроется главное окно редактора VBA с текстом записанного макроса, например:

 

Sub Staff()

‘

‘ Staff Макрос

' Штатное расписание больницы

‘

    Range(“I14”).Select

    Range(“I14”).GoalSeek Goal:=10000, ChangingCell:=Range(“H6”)

End Sub

 

Именно эта процедура и выполняется, если в диалоговом окне Макросы нажать кнопку Выполнить. Рассчитываются оклады для заданного заранее нового количества штатных единиц.

Для еще большей оптимизации действий по расчету штатного расписания разместим на листе кнопку, при нажатии на которую будут производиться нужные действия.

Кнопка является одним из элементов управления листа, создаваемых с помощью панели инструментов Формы. Обычно этой панели нет на экране, поэтому выполняем команду Сервис | Настройка | Панели инструментов | Формы. На экран выводится панель инструментов Формы (рис. 8.3). Выбираем на ней щелчком мыши форму Кнопка. При этом указатель мыши превращается в тонкий крестик. Щелкаем им по листу. На нем появляется кнопка с именем Кнопка1 и одновременно открывается диалоговое окно Назначение макроса объекту. В поле Имя макроса выбираем имя нашего макроса «Stuff».

Теперь указанная выше процедура расчета окладов будет выполняться простым нажатием кнопки.

Можно изменить формат кнопки (шрифт надписи, размер и т.п.). Для этого следует вызвать контекстно-зависимое меню и выполнить необходимые операции.

 

 


 

 

 

 

 

Лабораторная   работа   9.   Создание   отчетно  - аналитической ведомости о работе сети магазинов

 

Первичной информацией в этой работе является таблица выручки (в тыс. руб.) за январь, февраль, март шести магазинов торговой сети фирмы «Шмидт и сыновья», которую нужно построить самостоятельно, внеся данные от 500 до 2000 тыс. руб.

 

Задание

1. Используя функцию СУММ, подсчитать суммарную выручку каждого магазина и суммарную выручку в каждом месяце.

2. Принимая число 4000 тыс. руб. за плановую квартальную выручку, с помощью функции СЧЕТЕСЛИ подсчитать, сколько магазинов перевыполнили план.

2. Используя функцию СРЗНАЧ, подсчитать ежемесячную среднюю выручку  и среднюю выручку каждого магазина.

3. Используя функцию РАНГ, подсчитать место каждого магазина по объему продаж.

4. Подсчитать для данного множества суммарных выручек магазинов, сколько значений попадает в интервалы от 0 до 1000, от 1001 до 2000, от 2001 до 3000, от 3001 до 4000 и свыше 4000 тыс. руб., используя функцию ЧАСТОТА.

Функция ЧАСТОТА возвращает распределение частот в виде вертикального массива. Исходными данными являются массив данных, для которых вычисляются частоты, и множество интервалов (массив карманов), в которых группируются значения из массива данных. Для работы с этой функцией необходимо сначала выделить область, куда попадут результаты вычисления, а после задания исходных данных в поле функции выйти не как обычно, нажатием клавиши Enter или кнопки ОК,  а нажатием клавиш Ctrl + Shift + Enter.

5. Вычислить эти же частоты с помощью диалогового окна Анализ  данных  (Сервис  |  Анализ  данных | Гистограмма) (рис. 9.1, 9.2).

Если в меню Сервис отсутствует команда Анализ данных, то для ее установки нужно выполнить последовательность действий: Сервис | Надстройки | Analysis Toolpak.

6. Построить гистограмму ЧАСТОТА (ОБЪЕМ РЕАЛИЗАЦИИ) и диаграмму ВЫРУЧКА МАГАЗИНОВ (в процентах) с помощью Мастера диаграмм.

 


Примечание.  Если процесс создания отчетно-аналитической ведомости записать в виде макроса (например, с помощью MacroRecoder, то при его вызове на активном рабочем листе будет автоматически создаваться шаблон таблицы. Если в нее внести новые данные, то расчет и построение диаграмм будет происходить автоматически.

 

Лабораторная работа 10. Некоторые финансовые функции Excel

 

Финансовые расчеты, проводимые с помощью встроенных финансовых функций Excel, можно разделить на четыре группы:

наращение и дисконтирование доходов и затрат (БЗ, ПЗ, КПЕР, НОРМА, ППЛАТ и др.);

анализ эффективности капитальных вложений (НПЗ, ВНДОХ и др.);

расчеты по ценным бумагам (ДОХОД, ЦЕНА и др.);

расчет амортизационных отчислений (АМР, АМГД и др.).

Всего в Excel встроено более 50 финансовых функций. Рассмотрим применение некоторых из них.

 

Функция БЗ. Возвращает будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки (наращение из настоящего в будущее). Для расчета функции БЗ используется метод сложных процентов.

Ее вид:

БЗ (Норма; Кпер; Выплата; Нз; Тип)

Аргументы:

Норма – процентная ставка за период (задавать в процентном формате или в долях);

Кпер – общее число платежных периодов, по истечении которых вы хотите определить объем имеющихся средств;

Выплата – величина постоянных периодических платежей;

Нз – начальное значение (текущая стоимость) вклада;

Тип – параметр, определяющий, когда вносятся платежи: в начале (=0) или в конце периода (=1). По умолчанию Тип=0.

 

Функция БЗРАСПИС. Возвращает будущее значение единовременного вложения при переменной процентной ставке.

Ее вид:

БЗРАСПИС (Первичное; План)

Аргументы:

Первичное – числовое значение, представляющее собой исходную сумму средств;

План – массив процентных ставок, используемых за рассматриваемый период.

 

Задание 1. В банк помещен депозит в размере А = 5000 руб. По этому депозиту в первом году будет начислено р1 = 10% , во втором – р2 = 12%,  в третьем – р3 = 15%, в четвертом и пятом – р4,5 = 16% годовых. Сколько будет на счету в конце пятого года? Сколько надо было бы поместить на счет при постоянной процентной ставке i = 13%, чтобы обеспечить ту же сумму.

Решить аналогичную задачу, взяв данные из таблицы 10.1.

Указание. Использовать сервисную функцию Excel Подбор параметра.

 

Таблица 10.1

Вариант

А

р1

р2

р3

р4

р5

i

1

2

3

4

5

6

7

8

9

10

11

12

1000

2000

3000

4000

5000

6000

7000

8000

9000

10000

11000

12000

3

4

5

6

7

8

9

10

11

12

13

14

4

6

6

7

7

9

9

10

12

13

14

15

5

7

7

8

8

10

10

11

13

14

15

15

6

8

9

8

8

11

11

12

14

15

16

16

7

9

10

9

10

12

12

10

15

16

16

17

5

7

9

6

7

11

9

5

4

6

8

9

 

Функция ПЗ. Возвращает текущий объем вклада на основе постоянных периодических платежей (или, иными словами, сумму всех будущих платежей).

Ее вид:

ПЗ (Норма, Кпер, Выплата, Бс, Тип)

Аргументы:

Норма – процентная ставка за период (задавать в процентном формате или в долях);

Кпер – общее число периодов выплат;

Выплата – величина постоянных периодических платежей;

Бс – баланс наличности, который нужно достичь после последней выплаты (если опущен, то 0);

Тип – 0 или 1. Если 0 – оплата производится в конце периода, если 1, то в начале.

Текущий объем вклада – это сегодняшний объем будущих платежей, например, это та сумма денег (ПЗ), которая будет выплачена заимодавцу через Кпер обусловленных периодов при Норма процентов годовых, если каждый период вносится постоянная сумма Выплата.

На рис 10.1 приведено диалоговое окно функции ПЗ, использованной для решения следующей задачи.

Сколько  вы  переплатите  за  холодильник  стоимостью 10 тыс. руб. при покупке его в рассрочку на 3 года под процентную ставку 5% при ежеквартальной выплате 1500 руб.

Ответ: почти 16619 – 10000 =6619 руб.


Рис. 10.1 – Диалоговое окно функции ПЗ

 

Примечание. При использовании финансовых функций необходимо соблюдать следующее правило: то, что вы платите, должно учитываться со знаком «–», а то, что вы получаете, – со знаком «+».

 

Задание 2. У вас просят в долг P=10000 руб. и обещают возвращать по A=2000 руб. в течение N=6 лет. У вас есть другой способ использования этих денег: положить их в банк под 7% годовых и каждый год снимать по 2000 руб. Какая финансовая операция будет более выгодна для вас? С помощью Диспетчера сценариев проанализировать ситуацию для нескольких возможных вариантов изменения параметров А и N, взяв их из таблицы 10.2.

Создание первого сценария производится с помощью последовательности команд Сервис | Сценарии | Диспетчер сценариев | Добавить (рис. 10.2).

В поле Изменяемые ячейки указываются те ячейки, в которых находятся параметры задачи.

Таблица 10.2

Вариант

1

2

3

4

5

6

7

8

9

10

11

12

N, год.

7

8

9

10

11

7

8

9

10

11

3

7

P,

тыс. р.

170

200

220

300

350

210

250

310

320

360

10

10


A,

тыс. р.

32

31

33

45

41

32

37

48

35

41

4,0

1,6

 

После нажатия кнопки ОК в диалоговом окне Значения ячеек сценария вводятся значения параметров для первого сценария, и с помощью диалогового окна Диспетчер сценариев (рис. 10.3) добавляется необходимое число сценариев.

С помощью кнопки Отчет открывается диалоговое окно Отчет по сценарию, где определяется тип отчета (Структура или Сводная таблица) и задаются ячейки, где вычисляется результат, т.е. значение функции ПЗ.

 

Функция НПЗ. Используется в Excel для расчета эффективности планируемых капиталовложений. Она возвращает чистую текущую величину вклада (инвестиции), вычисленного на основе ряда последовательных (неравномерных) поступлений денежных средств.

Вид функции:

НПЗ (Ставка; Значение1; Значение 2;...Значение N)

Аргументы:

Ставка – процентная ставка за период;

Значения – до 29 аргументов (могут быть массивы), представляющих поступления (доходы со знаком «+», расходы со знаком «–»).

Рассмотрим применение функции НПЗ для решения следующей задачи.

Пусть в начале первого года вы вкладываете в инвестиционный проект 30000 рублей и предполагаете годовые доходы 8000 руб., 9000 руб., 10000 руб., 12000 руб. в последующие четыре года (начиная со второго). Предположим, что годовая учетная ставка составляет 8 процентов, в таком случае чистый текущий объем инвестиции составит:

–30000+НПЗ(8%; 8000; 9000; 10000; 12000) =1882,14 руб.

Если платежи происходят в конце рассматриваемых периодов, то формула расчета чистого текущего объема инвестиции примет несколько другой вид:

НПЗ(8%; –30000; 8000; 9000; 10000; 12000) =1742,72 руб.,

т.е. первоначальные затраты 30000 руб. были включены в формулу одним из значений.

 

Задание 3. У вас есть возможность проинвестировать проект стоимостью A=10000 руб. Через год будет возвращено P1=2000 руб., через  два года - P2=4000 руб.,  через три года – P3=7000 руб.  Альтернативный вариант – положить деньги в банк под i процентов годовых. При какой годовой процентной ставке выгоднее вложить деньги в инвестиционный проект? Решить аналогичную задачу, взяв данные из таблицы 10.3.

Указание. Использовать сервисную функцию Excel Подбор параметра.

 

Таблица 10.3

Вариант

N

A

P1

P2

P3

P4

P5

1

2

3

4

5

6

7

8

9

10

11

12

3

4

5

3

4

5

3

4

5

3

4

5

17000

20000

22000

30000

35000

21000

25000

31000

32000

36000

26000

40000

5000

6000

5000

5000

5000

4000

8000

9000

8000

10000

7000

8000

7000

6000

8000

10000

9000

5000

9000

10000

10000

15000

10000

12000

8000

9000

8000

18000

10000

8000

10000

10000

10000

21000

11000

15000

 

7000

7000

 

18000

10000

 

15000

10000

 

10000

15000

 

 

5000

 

 

11000

 

 

11000

 

 

16000

 

 

Функция ППЛАТ. Вычисляет величину постоянной периодической выплаты ренты, регулярных платежей по займу и т.п. при постоянной процентной ставке. Она связана с функцией ПЗ: это то, что в ней называется Выплата. 

Вид функции:

ППЛАТ (Норма, Кпер, Пз, Бс, Тип)

Аргументы:

Пз –- общая сумма всех будущих платежей с настоящего момента;

остальные аргументы те же, что и для функции ПЗ.

 

 

Задание 4. Вычислить N - годичную ссуду покупки квартиры за А рублей  с годовой ставкой  i процентов  и  начальным взносом p процентов. Какова сумма выплаченных комиссионных? Сделать расчет для ежемесячных и ежегодных выплат. Данные взять из таблицы 10.4.

 

 

 

 

Таблица 10.4

Вариант

1

2

3

4

5

6

7

8

9

10

11

12

N, год.

7

8

9

10

11

7

8

9

10

11

7

8

А, тыс. р.

170

200

220

300

350

210

250

310

320

360

180

200

р, %.

10

10

20

20

15

15

30

30

25

25

25

15

i, %

5

6

7

8

9

10

11

12

13

14

10

8

 

Функция НОРМА. Эта функция вычисляет процентную ставку за один период, необходимую для получения определенной суммы в течение заданного срока путем постоянных взносов.

Ее вид:

НОРМА (Кпер, Выплата, Пз, Бс, Тип, Предположение)

Аргументы:

первые пять аргументов соответствуют аргументам функций ПЗ и НОРМА;

Предположение - предполагаемая величина нормы (поиск величины нормы организован итерационным способом и это значение есть начальное приближение); если опущено, то берется значение 10% .

 

Задание 5. Определить процентную ставку для N - летнего займа в А рублей с ежегодной выплатой в Р рублей. Данные взять из таблицы 10.5.

 

Таблица 10.5

Вариант

1

2

3

4

5

6

7

8

9

10

11

12

N, год.

5

6

7

8

10

10

12

15

20

30

40

55

А, млн.р.

1,0

0,8

0,8

0,8

1,7

1,0

7,5

5,9

10

30

35

6,5

Р, млн.р.

0,2

0,15

0,12

0,12

0,19

0,15

0,7

0,7

1,0

1,7

1,8

0,24

 

 

Лабораторная работа 11. Моделирование развития финансовой пирамиды

 

Развитие финансовой пирамиды во многом напоминает развитие эпидемии, когда число заболевших (купивших акции) в конкретный день пропорционально числу больных в городе (числу проданных акций) n, перемноженному на число еще не переболевших (не купивших акции) M-n. В случае эпидемии коэффициент пропорциональности зависит от мер профилактики. В случае финансовой пирамиды этот коэффициент (назовем его коэффициентом ажиотажа КА) зависит от уровня инфляции, рекламы, наличия других параллельных пирамид, от срока, прошедшего с  момента шумного краха предыдущей пирамиды, и т.д.

Тогда процесс можно описать обыкновенным дифференциальным уравнением

.

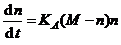Применяя к этому уравнению разностную схему Эйлера, получаем формулу для определения числа акций NKD+1, купленных жителями на (D+1)-й день (предположим, что один житель покупает одну акцию):

 

              NKD+1 = NKD + KA(M-NKD)NKD ,

 

где M - число жителей в городе, NKD - общее число купивших акции на день D.

За волной купивших акции идет волна желающих их сдать (продать) - вернуть свои «кровные» и причитающиеся дивиденды. Будем считать, что волна продающих акции отстает от волны их купивших на число дней Т.

Тогда число акций, проданных жителями в (D+1)-й день, можно оценить по формуле

 

              NPD+1 = 0, если D T,

              NPD+1 = NKD-T , если D > T.

 

Количество денег на счету организаторов пирамиды завтра (ПD+1) можно выразить через количество денег сегодня (ПD), если известен курс акций и количество покупок NKD  и продаж NPD акций населением.

Пусть динамика изменения курсов продажи и покупки рублевых акций выражается таблицей 11.1:

 

Таблица 11.1 – Курс покупки – продажи акций

Дни, прошедшие с начала эмиссии акций, D

1

2

3

¼

51

¼

365

¼

Курс продажи P(D), руб.

1,05

1,07

1,09

¼

2,05

¼

8,33

¼

Курс покупки K(D), руб.

1,00

1,02

1,04

¼

2,00

¼

8,28

¼

 

Тогда с учетом ежедневного дохода организатора пирамиды  (S процентов от суммы в кассе) и затрат на организацию пирамиды (налоги, оплата текущих расходов, реклама и т.п. – R рублей) имеем [4]:

 

ПD+1=ПD+NKD×P(D)–NPD×K(D)–ПD×S/100–R.

 

Задание

1. Построить таблицу, состоящую из следующих граф: День; Курс продаж; Продано в день; Продано всего; Курс покупки; Куплено в день; Куплено всего; Сумма в кассе; Доход в день; Доход всего. Исходные данные использовать с абсолютной адресацией, выбирая их из Таблицы исходных данных. Сдвиг волны «покупка-продажа» задать программно с помощью функций Excel из категории Ссылки и массивы.

2. Построить в одной системе координат графики изменения количества денег в кассе и изменения доходов организатора пирамиды, взяв реальный диапазон дней.

3. С помощью функций Excel определить сумму максимального дохода и день ее достижения.

4. Любое дело требует начальных расходов, иногда весьма существенных. С помощью сервисного средства Excel Подбор параметра подобрать такое минимальное значение начального капитала, которое бы позволило не уйти в «отрицательную сумму в кассе» на начальном этапе развития пирамиды.

5. Изменяя исходные данные, проследить за изменением дохода организатора (в каждом варианте меняется только один параметр!). Результаты исследований оформить в виде таблицы параметрического исследования модели (табл. 11.2). Сделать выводы.

 

 

Таблица 11.2 – Параметрическое исследование модели

Изменяемый

параметр

Увеличиваем параметр

Уменьшаем параметр

Значение

День Х

Доходы на день Х

Значение

День Х

Доходы на день Х

M

KA

...

 

 

 

 

 

 

 

 

Рекомендация. В работе использовать и описать функции Excel ПОИСКПОЗ, ВПР, СМЕЩ из категории Ссылки и массивы.

 

Исходные данные для расчета.

 

Число жителей в городе M=1000000.

Коэффициент ажиотажа КА=0,0000001.

Ежедневные расходы (руб.) R=300.

Среднее время между покупкой и продажей акции (дни) Т=50.

Норма прибыли (ежедневный процент от суммы в кассе) S=3.

Состояние на первый день:

- начальный капитал (руб.) П1=70000;

- число купивших акции в первый день SNK1=7.                     

 

 

 

 

 

 

 

 

Лабораторная работа 12. Задачи оптимизации

в экономике

 

Excel предлагает мощный инструмент для решения оптимизационных задач, то есть таких задач, в которых необходимо найти экстремальное значение (минимум или максимум) некоторой функции, называемой целевой, при заданных ограничениях.

Если целевая функция и/или ограничения – линейны, то такие задачи принято называть задачами линейного программирования.

Многие экономические задачи решаются в рамках линейного программирования. Целевой функцией в них является либо прибыль или объем производства, которые надо максимизировать, либо затраты (издержки), которые надо минимизировать. Ограничения – обычно это условия, которые накладываются на используемые ресурсы для производства продукции. Построив математическую модель и решив задачу в заданных ограничениях, можно поварьировать ограничениями, то есть речь уже идет о математическом моделировании экономических систем с помощью Excel.

Рассмотрим задачу.

В цехе площадью 74 м2 необходимо установить станки, на приобретение которых отпущено 420 тыс. руб.

Существует два типа станков. Станок первого типа стоимостью 60 тыс. руб., требующий 12 м2 производственных площадей, обеспечивает изготовление 70 изделий в смену. Аналогичные характеристики станка второго типа составляют соответственно 40 тыс. руб., 6 м2 , 40 изделий в смену.

Найти оптимальный вариант приобретения станков, обеспечивающий максимальное производство изделий в цехе.

Обозначим Х1 количество станков первого типа, а Х2 – количество станков второго типа, которые предполагается установить в цехе. Тогда количество изделий, которое будет произведено на этих станках равно

F(X1, X2)=70*X1+40*X2.

Это и есть целевая функция, которую нужно максимизировать.

Теперь запишем ограничения. Их в задаче два.

Ограничения по финансам:

60*X1+40*X2 £ 420 тыс. руб.

Ограничения по площади размещения:

12*X1+6*X2 £ 74 м2.

Кроме этих ограничений следует добавить очевидные ограничения:

- переменные задачи должны быть неотрицательные

X1 ³ 0; X2 ³ 0;

- переменные задачи должны быть целочисленные

X1, X2 Î Z.

Итак, математическая модель сформулирована.

 

Решение оптимизационных задач в Excel проводится с помощью специализированной программы Поиск решения, вызываемой из главного меню: Сервис | Поиск решения.  Она  находится  в файле SOLVER.XLA, который подключается при первом обращении к этой программе.  Эту  программу  мы уже использовали при нахождении  корней нелинейного уравнения  в лабораторной работе 4.

Таким образом, теперь задача состоит в том, чтобы перенести математическую модель в Excel.

Порядок действий следующий.

1. Отводим ячейки для каждой независимой переменной задачи. В нашем примере это ячейка B4 для Х1 и ячейка B5 для Х2  (рис. 12.1). Их можно оставить пустыми.

2. Отводим ячейку (С13) для целевой функции и набираем в ней соответствующую формулу:

= B4*E4+B5*E5.

В формуле в качестве переменных фигурируют адреса ячеек, где расположены соответствующие переменные. Константы задачи заданы не числами, а также ссылками на ячейки, в которых их необходимо предварительно разместить. Рекомендуется для этого оформить таблицу, например так, как это показано на рис. 12.1.

3. Отводим ячейки (А13 и В13) для создания формул, соответствующих левой части каждого ограничения:

=В4*С4+В5*С5

=В4*D4+B5*D5.

4. Открываем диалоговое окно Поиск решения (рис. 12.2).

5. В поле Установить целевую ячейку указываем адрес ячейки, в которой находится формула для расчета целевой функции (ячейка С13). Ниже указываем тип оптимизации (поиск максимума или минимума).

6. В поле Изменяя ячейки отмечаем адреса ячеек, где находятся независимые переменные задачи (В4 и В5).

 


7. Для того чтобы ввести ограничения, нужно нажать на кнопку Добавить . Появляется диалоговое окно Добавление ограничения (рис. 12.3).


В левое поле вводим адрес ячейки, где находятся ограничения (или диапазон адресов ячеек), в центральном поле выбираем знак операции отношения (а также задаем целочисленность или бинарность переменных), в правом поле задаем адрес ячейки (или диапазон адресов), где находятся правые части ограничений. Вместо адресов в правой части можно просто задать числовые значения.

Нажатием клавиши Добавить переходим в режим добавления следующего ограничения, нажатием клавиши ОК заканчиваем ввод ограничений.

Теперь, если необходимо, в поле Ограничения окна Поиск решения можно выбирать какие-либо ограничения и редактировать их или удалять.

8. Запускаем процесс вычислений нажатием кнопки Выполнить. Результат приведен на рис. 12.1. Заданным ограничениям удовлетворяет следующий парк станков: 3 – первого типа, 6 – второго типа; при этом будет изготовлено максимальное количество деталей – 450.

В окне Результаты поиска решения пользователю предлагается составить отчеты, полученные по результатам оптимального решения. Они будут располагаться на отдельных листах данной рабочей книги. С помощью этих отчетов можно получить информацию о степени дефицитности тех или иных ресурсов. Эти вопросы в данной лабораторной работе не рассматриваются, тем более, что для рассматриваемой целочисленной задачи отчет по результатам, например, не дает какой-либо дополнительной информации, а два других отчета закрыты.

В окне Поиск решения с помощью кнопки Параметры можно вызвать диалоговое окно Параметры поиска решения (рис. 12.4).

Рассмотрим элементы этого окна.

 


Поля Максимальное время и Предельное число итераций определяют время, отпущенное на поиск решения задачи, и число промежуточных вычислений, соответственно.

Поля Относительная погрешность, Допустимое отклонение и Сходимость служат для задания точности, с которой ищется решение (последнее используется только для нелинейных моделей). Рекомендуется после решения задачи повторить его с большей точностью (особенно для целочисленных моделей), чтобы проверить точность модели.

Флажок Линейная модель устанавливается для линейных задач и снимается для нелинейных.

Флажок Неотрицательные значения позволяет установить нулевую нижнюю границу для тех ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение.

Флажок Автоматическое масштабирование служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине, например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.

Флажок Показывать результаты итераций служит для пошагового проведения итераций с целью просмотра промежуточных результатов.

Опция Оценки служит для указания метода экстраполяции, используемого при поиске решения.

Опция Разности служит для указания метода численного дифференцирования, который используется для вычисления производных при поиске решения.

Опция Метод поиска служит для выбора алгоритма оптимизации (метод Ньютона или сопряженных градиентов) для указания направления поиска.

Более подробную информацию можно получить, нажав кнопку Справка в том же диалоговом окне.

 

 

Задание 1. Пусть уже построена математическая модель некоторой оптимизационной задачи. Найти оптимальное значение целевой функции R(x) при заданных ограничениях с помощью сервисной программы Excel Поиск решения.

 

1. R(x)= 626x1+ 656x2 ® mах  при ограничениях

5x1 + 8x2 £ 81; 6x1 + 4x2 £ 70; 3x1 + x2 £ 26; x1 + x2 £ 12;

x1 £ 8; x1, x2 ³ 0.

 

2. R(x)=–5x1 + 4x2–x3–3x4–5x5  ® min  при ограничениях

            3x1–x2 + 2x4 + x5 = 5; 2x1–3x2 + x3  + 2x4 + x5 = 6;

            3x1–x2 +x3 +3x4 + 2x5 = 9; xi ³ 0, i=1...5.

 

3. R(x)=–2x1 +x2 + 4x3–x4–x5 ® min  при ограничениях

            x2 + 2x4–x5 =1; x1–x4–x5 =1;

            2x2+x3 + 2x5 = 4; xi ³ 0, i=1...5.

 

4. R(x)= 2x1 + x2 + x3 + 7x4–2x5 ® min  при ограничениях

            x1 +x2–x3 + x4  = 1; 2x1 + x2 + x3 –x5 = 7;

            x1 + 2x2 + x3 –7x4 + x5 = 6; xi ³ 0, i=1...5.

 

5. R(x)=–x1 + x2 + x3 + x4 + 3x5 ® min  при ограничениях

            2x1+ 2x2+ x4 + x5 =3; 3x1 –x2 + 2x3 – 2x5 =1;

            –3x1 + 2x3 – x4 + 2x5 = 1; xi ³ 0, i=1...5.

 

6. R(x)= –4x1 +2x2 –x3 +x4 ® min  при ограничениях

            3x1 + 2x2 – x3 + 4x4  = 3; x1 – x2 + 4x3  – 2x4 = 2;

            xi ³ 0, i=1...4.

 

7. R(x)= x1 + 2x2 + x3 –x4 ® min  при ограничениях

            10x2 + x3 + 2x4 + 3x5 = 25; –x1 + 5x2 + x3  + x4 + x5 = 10;

            2x1 – x2 + x3 – 3x4  = 6; xi ³ 0, i=1...5.

 

8. R(x)= 4x1 –3x2 – x4 + x5 ® min  при ограничениях

            –x1 + 3x2 + x4  = 13;  4x1 + x2 + x5 = 2;

            –2x1 + x2 + x3  = 1;  x1 – 3x2 + x6 = 0; xi ³ 0, i=1...6.

 

9. R(x)= x1 – x2  ® mах  при ограничениях

            2x1 – 4x2 – x3 + x4 = –3; 4x1 – 3x2 – x3  + x4 + x5 = 6;

            x1 + 4x2 + x3 + x5 = 15; xi ³ 0, i=1...5.

 

10. R(x)= x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 ® min  при ограничениях

            x1 + x4  = 20; x2 + x5 = 50; x3 + x6 =30;

            x4 + x5 +x6 = 60; xi ³ 0, i=1...6.

 

11. R(x)= x1 + x2  ® mах  при ограничениях

            x1 + x2 ³ 1; x1 – x2 ³ –1; x1 – x2  £ 1;

            x1 £ 2;   x2 £ 2; xi ³ 0, i=1...2.

 

12. R(x)= 4x1 + 6x2  ® min  при ограничениях

            x1 + x2 £ 20; x1 + 3x2  ³ 30; 8x1 + 6x2 ³ 72;

            8x1 + 6x2  £ 128; xi ³ 0, i=1...2.

 

13. R(x)= 3x1 + 8x2  ® mах  при ограничениях

            x1 + 7x2 £ 57; 2x1 + 5x2  £ 42; 3x1 + 4x2 £ 56;

            2x1 + x2  £ 34; xi ³ 0, i=1...2.

 

 

14. R(x)= x12 + x22 – 10x1 – 15x2 ® min  при ограничениях

            2x1 + 3x2 £ 13; 2x1 + x2  £ 10; xi ³ 0, i=1...2.

 

15. R(x)= 3x12 + x22 + 3x1 – 2x2 ® min  при ограничениях

            x1 + 3x2 + x3 + x4  = 16; 3x1 – x2  – x3 + x4 = 4;

 xi ³ 0, i=1...4.

 

16. R(x)= x12 + x22 + x32 +x2 – 2x3  ® min  при ограничениях

            x1 + x2 + 2x3  £ 6; 3x1  + 2x2  +x3  £ 12; xi ³ 0, i=1...3.

 

17. R(x)= –2x1 + 2x2 – 3x3 + 3x4 ® min  при ограничениях

            x1 – 2x2 + x4  = 3; x2 + x3  – 2x4  = 5;

            3x2 +x4 + x5  = 6; xi ³ 0,  xi Î Z;  i=1...5.

 

18. R(x)= x1 –x2 + x3 – x4  ® mах  при ограничениях

            x1 + 2x3 + x4  = 8; x1 +x2  – x4  = 4;

            –x1 + 2x2 + x3 + 3x4  = 6; xi ³ 0, xi Î Z; i=1...4.

 

19. R(x)= x1 + 2x2  + x5  ® min  при ограничениях

            x1 + x2 + x3 +x4 + x5 = 5; x2 + x3  + x4 – x5  = 2;

            x3 – x4 + x5  = 1; xi ³ 0, xi Î Z; i=1...5.

 

20. R(x)= 4x1 + 3x2  ® mах  при ограничениях

            2x1 + 3x2 +x3  = 8; 4x1 + x2  + x4  = 10;

            xi ³ 0, xi Î Z; i=1...4.

 

21. R(x)=  – x3   ® min  при ограничениях

            –6x2 + 5x3 +x5  = 6; 7x2 – 4x3  + x4  = 4;

            x1 + x2 +x3  = 9; xi ³ 0, xi Î Z; i=1...5.

 

22. R(x)= 3x1 + 2x2 + x3 ® min  при ограничениях

            x1 + 3x2 +x3 ³ 10; 2x1 + 4x3  ³ 14; 2x2 + x3 ³ 7;

            xi ³ 0, xi Î Z; i=1...3.

 

23. R(x)= –2x1 – x2 – x3 ® min  при ограничениях

            x1 + 2x2 + 2x3 = 16; x1 + x2  £ 7; 3x1 + 2x2 ³ 18;

            xi ³ 0, xi Î Z; i=1...3.

 

24. R(x)= –4x1 – 3x2  ® min  при ограничениях

            4x1 + x2  £ 44; x1   £ 22; x2  £ 18;

            xi ³ 0, xi Î Z; i=1...2.

 

25. R(x)= –6x1 + 2x12 – 2x1x2 + 2x22 ® min  при ограничениях

            x1 + x2 £ 2; x1 + 3x2 £ 3; xi ³ 0, i=1...2.

 

26. R(x)= x1 + x2  ® mах  при ограничениях

0£ х1 + х2 £ 3; –1£ х1 – х2 £ 0; 0£ х1 £ 1; 0£ х2 £ 3;

 х1 , х2 ³ 0.

 

27. R(x)= 2x1 + x2  ® mах  при ограничениях

х1 + 2х2 £ –1; 2х1 + х2 £ 2; х1 – х2 £ –1; –2х1 – 2х2 £ 3;

3х1 + 3х2 £ –2; х1 , х2 ³ 0.

 

28. R(x)= x1 – x2  ® mах  при ограничениях

1£ х1 + х2 £ 2; 2£ х1 – 2х2 £ 3; 1£ 2х1 – х2 £ 2;

х1 , х2 ³ 0.

 

29. R(x)= –9x1 – 2x2  ® mах  при ограничениях

–х1 – х2 £ 0; –х1 + х2 £ 0; –3х1 – х2 £ 0; –4х1 + х2 £ –1;

 х1 , х2 ³ 0.

 

30. R(x)= 2x1 + 3x2  ® min  при ограничениях

х1 + х2 £ 4; 3х1 + х2 ³ 4; х1 + 5х2 ³ 4; х1  £ 3;

х2 £ 3; х1 , х2 ³ 0.

 

 

 

 

Задание 2. Сформулировать математическую модель предложенной задачи оптимизации (целевая функция, система ограничений). С использованием сервисной программы Excel Поиск решения найти оптимальное значение целевой функции. Результаты решения оформить в виде наглядных таблиц.

 

Задача 1. Для изготовления сплава из меди, олова и цинка в качестве сырья используют два сплава тех же металлов, отличающиеся составом и стоимостью. Данные об этих сплавах приведены в таблице.

 

Компоненты

Содержание компонентов, %

сплава

Сплав №1

Сплав №2

Медь

10

10

Олово

10

30

Цинк

80

60

Стоимость  1 кг

40 руб.

60 руб.

 

Получаемый сплав должен содержать не более 2 кг меди, не менее 3 кг олова, а содержание цинка может составлять от 7,2 до 12, 8 кг.

Обеспечить количества Xj , j=1,2 сплавов каждого вида, обеспечивающие получение нового сплава с минимальными затратами на сырье.

 

Задача 2. Для изготовления двух видов изделий А1 и А2 завод использует в качестве сырья алюминий и медь. На изготовлении изделий заняты токарные и фрезерные станки. Исходные данные задачи приведены в таблице.

 

Вид

Объем

Нормы расхода на 1 изделие

ресурсов

ресурсов

Изделие А1

Изделие А2

Алюминий ,кг

570

10

70

Медь, кг

420

20

50

Токарные станки, станко-час

5600

300

400

Фрезерные станки, станко-час

3400

200

100

Прибыль на 1 изделие, тыс.руб.

 

30

80

 

Определить количества Xj ,j=1,2  изделий Аj , которые необходимо изготовить для достижения максимальной прибыли.

 

 

 

Задача 3. Из одного города в другой ежедневно отправляются пассажирские и скорые поезда. В таблице указано количество вагонов в поездах различного типа и максимальное число пассажиров, на которое рассчитан вагон.

 

 

Поезда

Вагоны

Багажный

Почтовый

Плацкартный

Купейный

Мягкий

Скорый

1

1

5

6

3

Пассажирский

1

—

8

4

1

Парк вагонов

12

8

81

70

26

Число

пассажиров

 

—

 

—

 

58

 

40

 

32

 

Определить число скорых Х1 и пассажирских Х2 поездов, которые необходимо формировать ежедневно из имеющегося парка вагонов, чтобы число перевозимых пассажиров было максимальным.

 

Задача 4. В начале рабочего дня автобусного парка на линию выходит Х1 автобусов, через час к ним добавляется Х2 автобусов, еще через час – дополнительно Х3 машин.

Каждый автобус работает на маршруте непрерывно в течение 8 часов. Минимально необходимое число машин на линии в i-й час рабочего дня (i =1,2,...,10) равно bi . Превышение этого числа приводит к дополнительным издержкам в течение i-го часа в размере сi рублей на каждый дополнительный автобус.

Определить количества машин Х1 , Х2 , Х3 , выходящих на маршрут в первые часы рабочего дня, с таким расчетом, чтобы дополнительные издержки в течение всего рабочего дня были минимальными. Исходные данные приведены в таблице.

 

i

1

2

3

4

5

6

7

8

9

10

bi

10

20

22

23

25

22

20

15

10

5

ci

5

5

6

6

6

6

10

15

15

20

 

Задача 5. На товарных станциях С1 и С2 имеется по 30 комплектов мебели. Известно, что перевозка одного комплекта со станции С1 в магазины М1 , М2 , М3 стоит соответственно 10 руб., 30 руб., 50 руб., а стоимость перевозки со станции С2 в те же магазины - 20 руб., 50 руб., 40 руб. Необходимо доставить в каждый магазин по 20 комплектов мебели.

Составить план перевозок так, чтобы затраты на транспортировку мебели были наименьшими.

 

Откуда

Куда

Всего отправлено

В М1

В М2

В М3

Из С1

Х11

Х12

Х13

30

Из С2

Х21

Х22

Х23

30

Всего получено

20

20

20

60

 

Задача 6. Предприятие, располагающее ресурсами сырья трех видов Bi , i=1,2,3,  может производить продукцию четырех видов Aj , j=1,2,3,4. В таблице указаны затраты ресурсов Bi на изготовление 1 т продукции Aj , объем ресурсов и прибыль, получаемая от изготовления 1 т продукции Aj .

 

Вид сырья

Вид продукции

А1

А2

А3

А4

Объем ресурсов, т

В1

4

5

2

3

60

В2

30

14

18

22

400

В3

16

14

8

10

128

Прибыль, руб.

480

250

560

300

-

 

Определить ассортимент выпускаемой продукции, при котором полученная прибыль будет максимальной, при условии:

а) продукции А2 необходимо выпустить не менее 8 т, продукции А4 - не более 5 т, а продукции А1 и А3 - в отношении 2:1;

б) производственные издержки на 1 т продукции Аj , j=1...4, составляют соответственно 30, 90,120 и 60 руб., а суммарные издержки не должны превышать 960 руб.

 

Задача 7. Пусть вашей фирме необходимо заключить контракт на поставку товаров на некоторую сумму, меньшую или равную Р условных единиц. При этом имеется выбор из N партнеров, которые могут поставить товар на Ki условных единиц каждый. Ожидаемая прибыль от сделки с i-м партнером составляет Ci процентов от суммы заключенной сделки, но при этом риск от сделки с i-м партнером составляет Hi процентов от суммы сделки. Требуется определить наиболее выгодных партнеров и сумму сделки с каждым из них, обеспечив при этом максимальное значение прибыли при значении суммарного риска от сделок, не превышающего суммы прибыли.

Исходные данные приведены в таблице.

 

Параметры контракта

Фирмы

СтикС

КомплекТ

Тэтрон

ЭлекТ

Играм

Максимальная сумма контракта с фирмой Ki , у.е.

 

30000

 

20000

 

12000

 

15000

 

10000

Ожидаемая прибыль Ci, %

10

11

11,8

10

12

Возможные убытки Hi , %

8

8,5

8,85

8,2

9

Максимальная сумма контракта равна 50000 у.е.

 

Задача 8. Ваше предприятие выпускает телевизоры, музыкальные центры и акустические системы, используя общий склад комплектующих.  В связи с ограниченностью запаса необходимо найти оптимальное соотношение объемов выпуска изделий. Цель – получение максимальной прибыли.

Для обеспечения договоров с заказчиками необходимо выпускать не менее 100 единиц каждого наименования. Следует учитывать уменьшение удельной прибыли при увеличении объемов производства (в связи с дополнительными затратами на сбыт) по степенному закону (коэффициент отдачи к=0,9). Данные для расчета приведены в таблице.

 

Склад

Наименование

Телевизор

М. центр

Ак . сист.

Количество

Х1

Х2

Х3

Цена изделия

5000

4500

1500

Комплектующие

Кол-во

Использовано

Требуется деталей

Шасси

450

У1

1

1

0

Кинескоп

250

У2

1

0

0

Динамик

800

У3

2

2

1

Блок питания

450

У4

1

1

0

Электрическая плата

 

600

 

У5

 

2

 

1

 

1

 

 

Задача 9. Для работников с пятидневной рабочей неделей и двумя выходными подряд требуется составить график работы, обеспечивающий требуемый уровень обслуживания при наименьших затратах на оплату труда. Дневная оплата каждого работника – 40 руб.

 

Дни недели

Вс

Пн

Вт

Ср

Чт

Пт

Сб

Требуется

работников

 

22

 

17

 

13

 

14

 

15

 

18

 

24

 

Указание.  Разбить  всех  работников  на 7 групп и обозначить  Х1 - количество работников, отдыхающих в воскресенье-понедельник, Х2 - количество работников, отдыхающих в понедельник-вторник, и т.д.

 

Задача 10. Требуется минимизировать затраты на перевозку товаров от предприятий-производителей на торговые склады. При этом необходимо учесть возможности поставок каждого из производителей при максимальном удовлетворении запросов потребителей. Данные для расчета приведены в таблице.

Сколько необходимо сделать рейсов, если за один рейс можно перевезти 20 т груза.

 

Заводы

Произв. мощности, т

Затраты на перевозку от завода к складу, у.е./т

Томск

Новосибирск

Омск

Тюмень

1

2

3

320

260

280

20

10

22

20

8

18

16

6

18

18

5

20

Потребности

складов, т

 

100

 

200

 

140

 

300

 

Задача 11. Маркетологи фирмы установили, что между расходами на рекламу R (руб.) и числом продаж N (шт.) существует связь, выражаемая формулой

                        ,

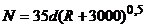где  коэффициент d - сезонная поправка.

Определить бюджет на рекламу в каждом квартале, соответствующий наибольшей прибыли за год, при фиксированных затратах на торговый персонал.  Оценить поквартально норму прибыли (отношение производственной прибыли к выручке от реализации). Годовые затраты на рекламу не должны превышать 40000 руб.  Цена  одного  изделия  -  40 руб.,  затраты  на  сбыт  одного  изделия - 25 руб.

 

Статьи

Квартал

За год

1

2

3

4

1. Сезонная поправка, d

0,9

1,1

0,8

1,2

—

2. Число продаж, N

?

?

?

?

?

3. Выручка от реализации

?

?

?

?

?

4. Затраты на сбыт

?

?

?

?

?

5. Валовая прибыль

?

?

?

?

?

6. Затраты на торговый персонал

8 000

8 000

9 000

9 000

34 000

7. Затраты на рекламу

R1

R2

R3

R4

R

8. Косвенные затраты (15% от ст. 3)

?

?

?

?

?

9. Суммарные затраты

?

?

?

?

?

10. Производств. прибыль

      (ст.5-ст.9)

 

?

 

?

 

?

 

?

 

?

11. Норма прибыли, %

?

?

?

?

?

 

Задача 12. Фабрика выпускает кожаные брюки, куртки и пальто специального назначения в ассортименте, заданном отношением 2:1:3.  В процессе изготовления изделия проходят три производственных участка - дубильный, раскройный и пошивочный.

Данные для расчета приведены в таблице.

 

Показатели

Брюки

Куртки

Пальто

Норма времени на участках, чел.×ч

 

 

 

         дубильном

0,3

0,4

0,6

         раскройном

0,4

0,4

0,7

         пошивочном

0,5

0,4

0,8

Полная себестоимость, руб.

15

40,5

97,8

Оптовая цена предприятия, руб.

17,5

42

100

 

Ограничения на фонд времени для участков составляют, соответственно, 3360, 2688, 5040 чел.×ч.  Учитывая заданный ассортимент, максимизировать прибыль от реализованной продукции.

 

Задача 13. На заводе ежемесячно скапливается около 14 т отходов металла, из которого можно штамповать большие и малые шайбы. Месячная потребность завода в больших шайбах 600 тыс. шт., в малых - 1100 тыс. шт. Расход металла на тысячу больших шайб - 22 кг, на тысячу малых - 8 кг. Для изготовления шайб используются два пресса холодной штамповки. Производительность каждого за смену 9 тыс. шт. больших шайб либо 11,5 тыс. шт. малых. Завод работает в две смены.

Недостающее количество шайб закупается. Оптовая цена больших шайб 11,9 руб. (за тысячу штук), а малых - 5,2 руб. Определить месячный план производства шайб, обеспечивающий максимальную долю в валовой продукции предприятия.

 

Задача 14. Цех мебельного комбината выпускает трельяжи, трюмо и тумбочки под телевизор.

Исходя из необходимости выполнения плана по ассортименту и возможности его перевыполнения по отдельным (или по всем) показателям, построить модели, на основе которых можно сформулировать следующие экстремальные задачи:

1) задачу максимизации объема реализации (за плановый период);

2) задачу максимизации прибыли (за тот же период).

Данные для расчета приведены в таблице. Определить недостающие данные и задать их самостоятельно.

 

Показатели

Трельяжи

Трюмо

Тумбочки

Норма расхода материала, м3

 

 

 

   ДСП

0,032

0,031

0,038

   Доски: сосновые

0,02

0,02

0,008

              березовые

0,005

0,005

0,006

Трудоемкость, чел. ч

10,2

7,5

5,8

Плановая себестоимость, руб.

88,81

63,98

29,6

Оптовая цена , руб.

93

67

30

Плановый ассортимент, шт.

350

290

1200

 

Задача 15. Предприятие выпускает обычный, специальный и декоративный сплавы латуни и реализует их, соответственно, по 3; 4,5 и 6 руб. за единицу веса. Его производственные мощности позволяют производить (за плановый период) не более 500 ед. веса обычного сплава, 700 ед. - специального и 250 ед. - декоративного. Обязательными составляющими сплавов являются медь, цинк, свинец и никель. Их цена соответственно 0,9; 0,7; 0,5 и 1,1 руб. за единицу веса.

По технологии декоративный сплав должен содержать не менее 7% никеля, 49% меди и не более 29% свинца; специальный  - не менее 3% никеля, 71% меди, 9% цинка и не более 21% свинца. В обычный сплав составляющие входят без ограничений.

Считая, что себестоимость сплавов складывается только из стоимости его ингредиентов, составить план выпуска сплавов, обеспечивающий максимальную прибыль.

 

Задача 16. Рацион стада крупного рогатого скота из 220 голов включает пищевые продукты A, B, C, D и E. В сутки одно животное должно съедать не менее 2 кг продукта вида А, 1,5 кг продукта В, 0,9 кг продукта С, 3 кг продукта D и 1,8 кг продукта Е. Однако в чистом  виде  указанные продукты  не производятся.  Они содержатся в концентратах К-1, К-2, К-3.  Их  цена и содержание  продуктов  (в процентах)  приведены в таблице.

 

Концентраты

Продукты, %

Цена, руб.

A

B

C

D

E

K-1

15

22

0

0

4

5

K-2

19

17

0

14

7

4

K-3

5

12

25

5

8

9

 

Минимизировать затраты на покупку концентратов при рациональном кормлении скота.

 

 

Задача 17. Нефтеперерабатывающий завод получает за плановый период четыре полуфабриката – 600 тыс. л алкилата, 316 тыс. л крекинг-бензина, 460 тыс. л бензина прямой перегонки и 200 тыс. л изопентана. В результате смешивания этих ингредиентов в пропорциях 2:3:1:5, 2:4:3:4:, 5:1:6:2 и 7:1:3:2 получают бензин четырех сортов Б-1, Б-2, Б-3, Б-4. Цена его реализации, соответственно, 2руб.; 2 руб.10 коп.; 2 руб.60 коп.; 2 руб.30 коп. за литр.

1. Спланировать ассортимент выпускаемой продукции, обеспечивающий максимальную прибыль.

2. Решить задачу, введя ограничение снизу на ассортимент продукции.

 

 

Задача 18. Для поддержания нормальной жизнедеятельности человеку ежедневно необходимо потреблять не менее 118 г белков, 56 г жиров, 500 г углеводов, 8 г минеральных солей. Количество питательных веществ, содержащихся в 1 кг каждого вида потребляемых продуктов, а также цена 1 кг каждого из этих продуктов приведены в таблицах.

Питательные вещества

Содержание питательных веществ в 1 кг продуктов, г

Мясо

Рыба

Молоко

Масло

Сыр

Крупа

Картофель

Белки

Жиры

Углеводы

Минеральные соли

180

20

-

 

9

190

3

-

 

10

30

40

50

 

7

10

865

6

 

12

260

310

20

 

60

130

30

650

 

20

21

2

200

 

10

 

Цена за 1 кг продуктов, руб.

Мясо

Рыба

Молоко

Масло

Сыр

Крупа

Картофель

31,8

21

4,28

58,3

67,5

8,1

2,5

 

Составить дневной рацион, содержащий не менее минимальной суточной нормы питательных веществ, необходимых человеку, так, чтобы общая стоимость продуктов была минимальной.

 

Задача 19. Четверо рабочих могут выполнять четыре вида работ. Стоимости Сij  выполнения i-м рабочим j-й работы приведены в таблице.

 

Рабочие (i)

Стоимость отдельных видов работ (j), у.е.

1

2

3

4

1. Иванов

2. Петров

3. Сидоров

4. Кузнецов

1

9

4

8

4

10

5

7

6

7

11

8

3

9

7

5

 

Необходимо составить план работ так, чтобы все работы были выполнены, каждый рабочий был загружен только на одной работе, а суммарная стоимость выполнения всех работ была минимальной.

 

Задача 20.  Небольшая фабрика выпускает два типа красок: для внутренних (В) и наружных (Н) работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта А и Б. Максимально возможные суточные запасы этих продуктов составляет 6 и 8 тонн, соответственно. Расходы продуктов А и Б на 1 т соответствующих красок приведены в таблице.

 

Исходный продукт

Расход исходных продуктов на тонну краски, т

Максимально возможный запас, т

В

Н

А

Б

2

1

1

2

6

8

 

Маркетинговые исследования установили, что суточный спрос на краску В никогда не превышает спроса на краску Н более, чем на 1 т. Кроме того, спрос на краску В никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 20000 руб. для краски В и 30000 руб. для краски Н.

Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

 

Задача 21. Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуется 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна 30 и 20 долл., соответственно.

Определить оптимальный суточный объем производства первой и второй моделей.

 

Задача 22. Фирма имеет возможность рекламировать свою продукцию, используя местное радио и телевидение. Затраты на рекламу в бюджете фирмы ограничены суммой $ 1000 в месяц. Каждая минута радиорекламы обходится в $ 5, а каждая минута телерекламы – в $ 100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем телевидение. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше объема сбыта, обеспечиваемого одной минутой радиорекламы.

Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.

 

Задача 23. Фирма имеет 4 фабрики и 5 центров распределения ее товаров. Фабрики фирмы расположены в Томске, Новосибирске, Ачинске и Саяногорске с производственными возможностями, соответственно, 200, 150, 225 и 175 единиц продукции ежедневно. Центры распределения товаров фирмы располагаются в Томске, Красноярске, Абакане, Барнауле и Стрежевом с потребностями, соответственно, в 100, 200, 50, 250 и 150 единиц продукции ежедневно. Хранение на фабрике единицы продукции, не поставленной в центр распределения, обходится в $ 0,75 в день, а штраф за просроченную поставку единицы продукции, заказанной потребителем  в  центр распределения,  но там не находящейся,  равен $ 2,5 в день.

Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в таблице.

 

Центры

производства

Транспортные расходы, $

Томск

Красноярск

Абакан

Барнаул

Стрежевой

Томск

Новосибирск

Ачинск

Саяногорск

0,5

0,9

1,2

2,5

1,5

1,7

1,1

1,2

2

2,5

1,5

0,7

2

1,1

2,3

2,7

1,5

1,5

2,0

2,8

 

Необходимо спланировать перевозки, обеспечив минимум транспортных расходов: а) при сбалансированной модели; б) при несбалансированной модели (перепроизводство или дефицит).

 

Задача 24. Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до восьминедельного возраста и после соответствующей обработки поступают в продажу. Будем считать, что в среднем недельный рацион одного цыпленка составляет 500 граммов.

Для того, чтобы цыплята достигли к восьмой неделе необходимого веса, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничимся рассмотрением только трех ингредиентов: известняка, зерна и соевых бобов. В таблице приведены данные, характеризующие содержание питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.

 

Ингредиент

Содержание питательных веществ, %

Стоимость, $/кг

Кальций

Белок

Клетчатка

Известняк

Зерно

Соевые бобы

38

0,1

0,2

-

9

5

-

2

8

0,08

0,30

0,80

 

Смесь должна содержать не менее 0,8% и не более 1,2% кальция, не менее 22% белка и не более 5% клетчатки.

Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости, при соблюдении требований к общему расходу кормовой смеси и ее питательности.

 

Задача 25. Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков приведено в таблице.

 

Станок

Время обработки одного изделия, ч

Тип 1

Тип 2

Тип 3

Тип 4

1

2

2

3

3

2

4

1

2

2

 

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет 10 и 15 долл. для станков 1 и 2, соответственно. Допустимое время использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1, 2, 3 и 4 равны 65, 70, 55 и 45 долл., соответственно.

Составить план производства, максимизирующий чистую прибыль.

 

Задача 26. Фирма производит два вида продукции – А и В. Объем сбыта продукции А составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции А составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны 20 и 40 долл., соответственно.

Определить оптимальное распределение сырья для изготовления продукции А и В.

 

Задача 27. Завод получает 4 вида полуфабрикатов Вi в количествах: В1 – 400 т, В2 – 250 т, В3 – 350 т и В4 – 100 т. В результате смешения этих компонентов получают 3 вида продукции Аj. Пропорции смешиваемых полуфабрикатов следующие: для А1 – 2:3:5:2, для А2 – 3:1:2:1, для А3 – 2:2:1:3. Стоимость 1 т продукции Аj составляет: А1 – 1200 руб., А2 – 1000 руб., А3 – 1500 руб.

Составить оптимальный план выпуска продукции по критерию:

1) максимальной стоимости выпущенной продукции;

2) максимального использования полуфабрикатов.

 

Задача 28. В цехе размещены 100 станков 1-го типа и 200 станков 2-го типа, на каждом из которых можно производить детали А1 и А2 . Производительность станков в сутки, стоимость 1 детали каждого вида и минимальный суточный план их выпуска представлены в таблице.

 

Детали

Производительность станков, дет./сут

Стоимость

одной детали, руб.

Минимальный суточный план

Тип 1

Тип 2

А1

А2

20

35

15

30

6

4

1510

4500

 

Найти количества станков i-го типа, которые необходимо выделить для производства деталей АJ, с таким расчетом, чтобы стоимость продукции, производимой в сутки, была максимальной.

 

Задача 29.  На заготовительный участок поступили стальные прутья длиной 111 см. Необходимо разрезать их на заготовки по 19, 23 и 30 см. Этих заготовок требуется, соответственно, 311, 215 и 190 шт. Построить экстремальную задачу выбора варианта выполнения этой работы, при котором число разрезаемых прутьев минимально.

 

Задача 30. На заготовительный участок поступило 69 металлических прутьев длиной 107 см. Их необходимо разрезать на заготовки по 13, 15 и 31 см в комплектности, задаваемой отношением 1:4:2. Построить модель, на основе которой можно сформулировать экстремальную задачу максимизации комплектов заготовок.

 

Указание к задачам 29, 30. Стандартная методика решения задач раскройного типа заключается в составлении возможных вариантов раскроя (для этого оформляется отдельная таблица) и постановке экстремальной задачи выбора их наилучшей комбинации по заданному критерию.

Литература

 

Гарнаев А.Ю. Использование MS Excel и VBA в экономике и финансах. – С-Пб.: БХВ – Санкт-Петербург, 1999. – 336 с.

Матвеев Л.А. Компьютерная поддержка решений. – С-Пб.: Специальная литература, 1998. – 472 с.

Овчаренко Е.К., Ильина О.П., Балыбердин Е.В. Финансово-экономические расчеты в Excel. Изд. 3-е. – М.:Филинъ, 1999. – 328 с.

Гусева О.Л., Миронова Н.Н. Excel для Windows. Практические работы //Информатика и образование. – 1996. – №2–6.

Капустин В.Ф. Практические занятия по курсу математического программирования. – Л.: Изд-во ЛГУ, 1976. – 192 с.

 

СОДЕРЖАНИЕ

Введение

ЛАБОРАТОРНАЯ  РАБОТА 1.  Изучение  основ  Excel. Заполнение таблиц

ЛАБОРАТОРНАЯ   РАБОТА 2. Построение диаграмм и графиков функций

ЛАБОРАТОРНАЯ  РАБОТА 3.  Трендовый анализ

ЛАБОРАТОРНАЯ  РАБОТА 4.  Численное  решение  уравнений

ЛАБОРАТОРНАЯ  РАБОТА 5. Электронная таблица как база данных. Сортировка и фильтрация данных

ЛАБОРАТОРНАЯ   РАБОТА 6. Сводные таблицы

ЛАБОРАТОРНАЯ  РАБОТА 7. Консолидация данных (связь таблиц)

ЛАБОРАТОРНАЯ  РАБОТА 8.  Составление штатного расписания больницы. Создание простых макросов

ЛАБОРАТОРНАЯ   РАБОТА   9.  Создание   отчетно– аналитической ведомости о работе сети магазинов

ЛАБОРАТОРНАЯ  РАБОТА 10. Некоторые финансовые функции Excel

ЛАБОРАТОРНАЯ  РАБОТА 11. Моделирование развития финансовой пирамиды

ЛАБОРАТОРНАЯ  РАБОТА 12. Задачи оптимизации в экономике

Литература

 

    3

 

    5

 

  28

  38

 

  45

 

  60

  64

 

  66

 

  69

 

  73

 

  79

 

  82

 

  87

108

 

 

 

 

 

 


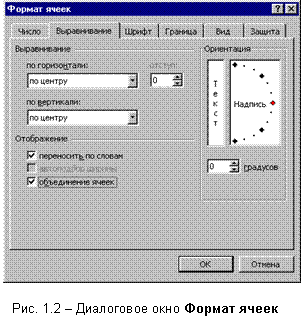
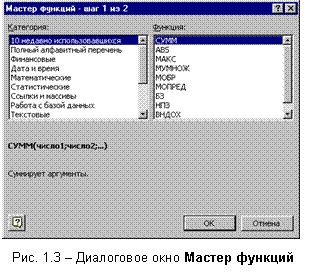
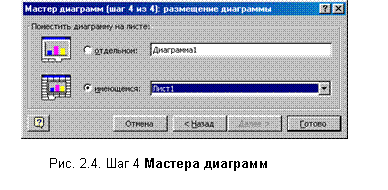
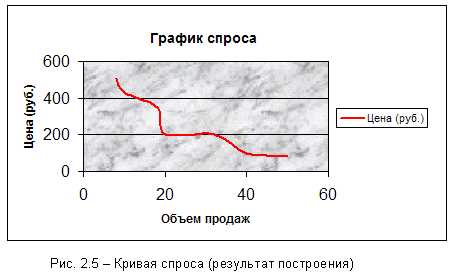
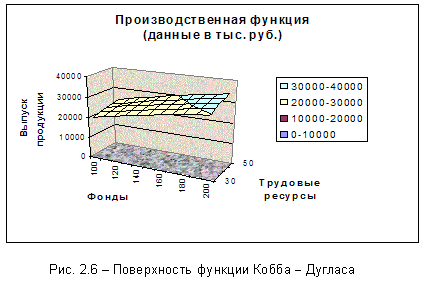
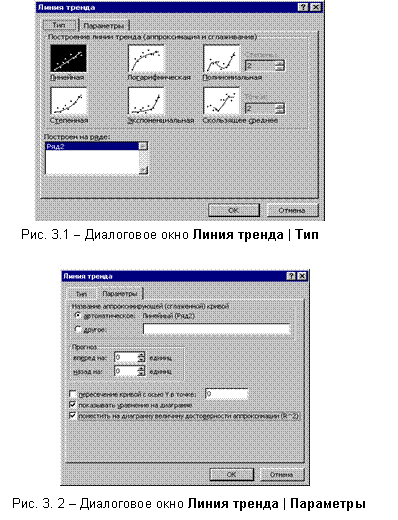
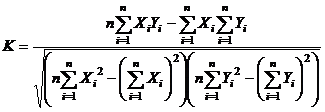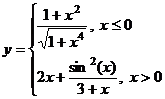
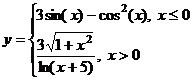
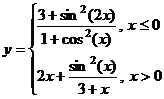
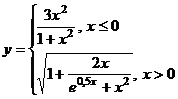
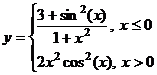
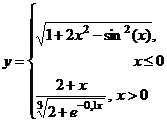
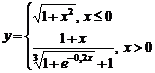
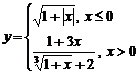
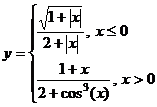
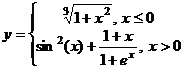
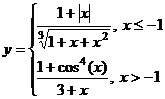
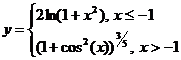
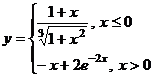
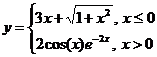
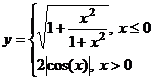
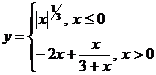
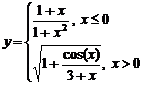
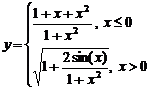
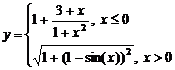
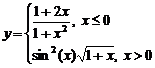
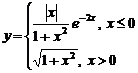
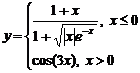
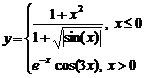
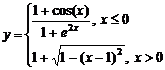
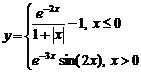
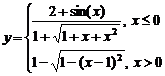
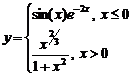
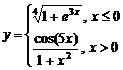
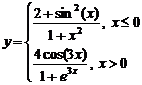
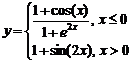
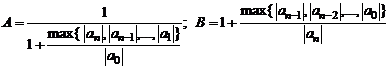[1] Visible Calculator (Наглядный калькулятор).

[2] Не правда ли, удачное название, связанное с игрой слов: Excellent – прекрасный, Cell – ячейка, Excel – превосходить.

[3] Кроме этой программы также известны электронные таблицы Lotus 1-2-3 (фирма Lotus Development), Quattro Pro (фирма Word Perfect – Novell Applications Group), SuperCalc (фирма Computer Associates). Но лидирующее положение (80% всех объемов продаж) занимает Excel.

[4] Очков В.Ф. Mathcad PLUS 6.0 для студентов и инженеров. – М.:КомпьютерПресс, 1996. – 238 с.