1. Основные термодинамические параметры и газовые законы

Исторически термодинамика возникла в XIX веке в связи с необходимостью изучения закономерностей процессов протекающих в паровых машинах. В настоящее время под технической термодинамикой понимается наука, изучающая процессы взаимного превращения теплоты и работы, а так же физические свойства тел, участвующих в этих преобразования [1].

Основными рабочими телами являются газообразные вещества - газы и пары, которые способны изменять свой объём в зависимости от изменения внешних условий. Рабочее тело в тепловой машине получает или отдаёт теплоту, взаимодействуя с более нагретым или более холодным внешними телами, которые называются источниками теплоты. Источник, который отдаёт теплоту рабочему телу и не изменяет свою температуру, называется верхним источником теплоты (ВИТ), а источник, получающий теплоту от рабочего тела и не изменяющий свою температуру, называется нижним источником теплоты (НИТ).

В зависимости от внешних условий один и тот же газ может находиться в различных состояниях, причём каждое из таких состояний характеризуется конкретными значениями ряда микроскопических величин, называемых термодинамическими параметрами. Это означает, что каждому состоянию газа соответствует одно и только одно значение каждого из термодинамических параметров.

Чтобы однозначно характеризовать состояние газа, необходимо и достаточно задать значения трёх любых его параметров таких, которые имеют конкретный физических смысл и достаточно просто измеряются техническими средствами. Такими термическими параметрами являются абсолютное давление, абсолютная температура и удельный объём.  Если эти параметры имеют одинаковые значения по всему объёму рабочего тела, то они называются  равновесными.

Абсолютное давление газа  представляет собой средний результат силового воздействия молекул на стенки сосуда и равно отношению нормальной составляющей силы F к площади S, на которую действует сила, т.е.

                                                     ,                                                           

В системе единиц СИ  давление измеряется в Па:

1 Па = 1 Н/м ²  = 10^-6 МПа

В практической гидравлике и теплотехнике давление принято измерять в атмосферах        (ат).

1ат = 1 кгс/см² = 0,1 МПа

Малые по величине давления часто измеряют высотой столба рабочей жидкости (ртути, воды и др.). Тогда для вычисления величины давления используется следующее соотношения:

1 ат = 760 мм рт.ст. = 10333 мм вод.ст.

В физике принято считать, что в среднем на уровне моря при температуре 0^оС давление равно 760 мм рт.ст. Величина такого давления называется физической атмосферой или нормальным атмосферным давлением и обозначается p_a.

Для измерения давления в технике обычно используются механические манометры, которые измеряют избыточное давление  (p_изб.), называемое обычно рабочим, или манометрическим давлением. Если измеряемое абсолютное давление выше нормального атмосферного, то:

                                           p_изб. = p_абс. – p_а                                                                                     (1.1)

При измерении давления вакуума (р_вак.), или разряжения слагаемые в левой части (1.1) меняются местами:

                                       p_вак. = p_а – p_абс..                                                                                 (1.2)

Следует иметь в виду, что в уравнения термодинамики входит абсолютное давление, выраженное в Паскалях. Это объясняется тем, что избыточное давление и разряжение при одном и том же абсолютном давлении  могут принимать различные значения в зависимости от величины нормального атмосферного давления, которое зависит от высоты рассматриваемой точки над уровнем моря.

Одним из основных параметров рабочего тела, определяющих его термодинамическое состояние,  является  температура. В соответствии с молекулярно-кинетической теорией абсолютная температура тела Т  понимается как мера интенсивности теплового движения молекул и определяется средней кинетической энергией движения молекул газа по уравнению (1.3):

                                            ,                                                (1.3)

где:      - масса молекулы;

   - средняя квадратичная скорость поступательного движения молекул;  

    - постоянная Больцмана (=1,38 · 10^-23  Дж/град)

Из уравнения (1.3) следует: при   = 0 скорость   = 0, т.е. при нуле градусов Кельвина  всякое движение молекул прекращается.

ГОСТ 8550-83 предусматривает применение в России двух температурных шкал: термодинамической (теоретической) и международной практической, основанной на  реперных точках: 0^○С  и 100^оС. В термодинамических расчетах всегда используется температура по шкале Кельвина ( ^○К), которая является параметром состояния, однако приборы для измерения температуры градуируются по шкале Цельсия (t^○C). Между этими шкалами существует простая зависимость: T = t + 273,15. Отметим, что в этих шкалах сдвинуты между собой нулевые точки, а величина градусов в них одинаковы, т.е.  

DΤ° Κ= D t° C.

На начальном этапе развития термодинамики использовались различные эмпирические температуры шкалы, в основном для термометров, работающих на основе зависимости объёма жидкости от её температуры. К таким шкалам относятся шкалы Реомюра, Фаренгейта, Ренкина, которые и сейчас иногда применяются в США и странах Западной Европы.

По шкале Реомюра температура измеряется в градусах Реомюра (°R), а в качестве реперных точек выбраны точки таяния льда O°R и точки кипения

воды 80^○ R. Пересчет значений температуры по этим шкалам производится в следующем соотношении: 1°R = 1,25°С.        

Шкала Фаренгейта, часто используется в США, также эмпирическая. Температура в ней измеряется в градусах Фаренгейта (°F), а реперные точки следующие:

0°F   – тройная точка (лёд, соль, нашатырь);

96°F – нормальная температура тела человека.

Тогда: 32°F - точка таяния льда;

           212°F         - точка кипения воды.

Пересчет одного градуса осуществляется по выражению 1°F =°С, а значения температур пересчитываются по более сложной формуле:

 t = ( F – 32).

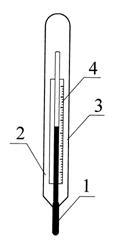
По шкале Ренкина размер градуса равен градусу Фаренгейта, но отсчет температуры производится от абсолютного нуля. Эта шкала сохранилась в США и некоторых странах, где принято измерять температуру в градусах Фаренгейта. Перевод температуры Ренкина в температуру Кельвина осуществляется по соотношению  Т = 5,9 F, где Т – температура Кельвина; F – температура Ренкина.

Измерить температуру, как среднюю скорость движения молекул, прямым способом не представляется возможным, поэтому для измерения температуры тела используются косвенные методы измерений, основанные на сравнении степеней нагретости двух тел. Для измерения  небольших температур (до 100°С) на практике используются жидкостные и газовые термометры, основанные на объёмном расширении рабочих тел при нагревании. Примером может служить стеклянно-жидкостной термометр с вложенной шкалой (рис. 1.1)  

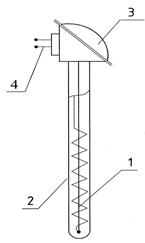
методами. В этих  системах в качестве первичных преобразователей (датчиков) используются термометры сопротивления  типов ТСМ, ТСП и др. и термометры ТХК, ТХА. В термометрах сопротивления используется зависимость электрического сопротивления проводника, например, медного или платинового, от температуры. Конструкция термометра сопротивления приведена на рис. 1.2.

         В термопарах, используемых в качестве чувствительных элементов при измерении больших температур, реализуется зависимость электродвижущей силы термопары (выдаваемого напряжения) от  температуры. Конструкции термопар аналогичны конструкциям термометра сопротивления, но в них чувствительным элементом является

не электрический проводник, а спай из двух разнородных сплавов. Вторичными приборами в системах автоматического контроля температуры для термометров сопротивления являются мосты, а для термопар – потенциометры.  

Известно, что величина, обратная удельному объёму, т.е. массе газа, заключенная в 1 м³, называется плотностью    и определяется по формуле (1.4):                                                =     кг/м³                                                              (1.4)

Использование удельного объема в качестве характеристики количества газа позволяет значительно упростить теплотехнические расчёты.

Важной теплотехнической характеристикой рабочего тела является теплоёмкость, определяющая его способность к нагреванию. Теплоёмкостью  называется          количество теплоты,  которое необходимо сообщить единице количества газа для изменения  его температуры на 1°С.         

В зависимости от единицы количества газа теплоёмкости могут быть массовые, объёмные и мольные. Наиболее часто используется массовая теплоёмкость, она обозначается буквой с  и измеряется  в  .

Известно, что количество передаваемой теплоты зависит от характера термодинамического процесса. В изобарном процессе  ( = const) передаётся значительно большее количество теплоты,  чем в изохорном ( = const). Отсюда следует, что для одного газа изобарная теплоёмкость с_р будет отличаться от изохорной с_v, а связь между ними определяется уравнением Майера:  с_р  = с_v+ R, где  R – газовая постоянная исследуемого газа.

Наряду с уравнением Майера взаимосвязь между этими теплоёмкостями часто выражают  через показатель адиабаты k, т.е. k =  . Значение k  зависит от количества атомов в молекуле газа, например, для двух атомных  газа  k = 1,4.

Для описания состояния газа простыми аналитическими зависимостями с использованием термических параметров состояния в термодинамике принята теоретическая модель идеального газа. Идеальным называется газ, у которого отсутствуют силы взаимного притяжения и отталкивания между молекулами, а их размеры намного меньше межмолекулярных расстояний.

Исследуемые в технике реальные газы, такие как воздух, кислород, водород, азот и др., при относительно низких температурах и высоких давлениях близки по своим свойствам к идеальным газам и их состояния с достаточно высокой точностью могут быть описаны газовыми законами.

Исторически газовые законы устанавливались опытным путём и формировались для двух переменных термических параметров, а третий параметр принимался постоянным.           Закон Бойля-Мариотта сформулирован для постоянной  температуры       (Т₁ = Т₂). Опытным путём установлено, что если постоянное количество газа, например     1 кг, при постоянной температуре переходит из одного состояния с параметрами p₁ и v ₁  в другое состояние с  параметрами  p₂ и v_2,, то его давление будет измеряться обратно пропорционально объёму:

                                                                                                   (1.5)

                или                      р₁ v₁ = p₂ v₂ = const                                  (1.6)

Из уравнения (1.6) следует,  что для любого состояния газа при T = const  произведение давления на объём данной массы газа есть величина постоянная.

Гей-Люссак сформулировал закон перехода газа из одного состояния в другое при постоянном давлении. Он установил, что если нагревать или охлаждать газ при р₁₌ p₂, то объём данной массы газа будет измеряться прямо пропорционально его абсолютной температуре. Тогда для 1 кг  можно записать:

                                                                                                                  (1.7)

В термодинамике количество вещества, наряду с массой, принято измерять в молях. Моль – это количество газа в граммах равное числу единиц молекулярной массы (). Связь между плотностями газа и молекулярными массами устанавливает закон Авагадро, который гласит: в равных объёмах различных газов содержится одинаковое число молекул, если эти газы имеют одинаковые температуры и давление. Из закона Авагадро следует, что при одинаковых температурах и давлениях плотность газов () пропорциональны их молекулярным массам:

                                                                                                    (1.8)        

Т.к. =1/ν, то  или idem                                 (1.9)

При нормальных условиях (= 760 мм рт.ст.и t = 0°С) уравнение (1.9) примет следующий вид:      

                                                  ,                                           (1.10)

   т.е. 1 кмоль любого газа при нормальных условиях занимает объём 22,4 м³.

Большой вклад в развитие термодинамики внёс Клайперон, который в 1834 году на основе опытных законов Бойля-Мариотта и Гей-Люссака для описания равновесных состояний идеального газа вывел уравнения, определяющие взаимосвязь между тремя термическими параметрами состояния ,и T . Это уравнения называется уравнением состояния идеального газа и имеют следующий вид:

                 для 1 кг газа :          рν =RT                                                         (1.11)

           для М кг газа :    рV =МRT,                                                        (1.12)

   где V – объём газа, м³; R – газовая постоянная, .

Газовая постоянная R для различных газов имеют разные значения, что усложняет расчёты. Несколько позже Д.И.Менделеевым было предложено универсальное уравнение состояния для 1 кмоля  газа, которое называется уравнением Менделеева-Клайперона:

                                                 p,                                                            (1.13)

    где     - объём одного киломоля, ,

         R – универсальная газовая постоянная,

Отметим, что универсальная газовая постоянная для всех газов имеет одинаковое значение при одинаковых температурах и давлениях. Так при нормальных условиях       R = 8314 .

С физической точки зрения величина R  представляет собой работу, которую совершает 1 кмоль газа при изменении температуры на 1°К.

Применение уравнений состояния идеальных газов (1.11.- 1.13) при расчётах реальных газов, например, водяного пара, широко используемого в тепловых машинах, даёт большие погрешности. В этих уравнениях не учитывается объём занимаемый   молекулами газа и силы их сцепления. Из известных эмпирических уравнений для расчёта реальных газов наиболее точным является уравнение Ван-дер-Ваальса, которое имеет вид:

                                                 () () = RT,                               (1.14)

    здесь  - величина, учитывающая силы взаимодействия между молекулами;

            b   - величина, учитывающая объём молекулы газа.

Уравнение Ван-дер-Ваальса рекомендуется использовать при сравнительно низких давлениях и высоких температурах, где точность расчётов по

этому уравнению достаточно высока.

Наряду с термическими параметрами состояния рабочего тела (р,ν,Т) в термодинамике широко используются калорические параметры к которым относятся:

         - внутренняя энергия (U);

         - энтальпия (I);

         - энтропия (S).

Внутренняя  энергия является функцией параметров состояния и подразделяется на кинетическую и потенциальную  (U = U_{к +} U_п). Кинетическая  энергия зависит от скорости движения молекул и состоит из энергии поступательного и вращательного движения молекул, а также колебательного движения атомов в самих молекулах. Согласно кинетической теории перечисленные виды энергии зависят только от температуры. Внутренняя потенциальная энергия обуславливается силами взаимодействия между молекулами и зависит от расстояния между ними и, следовательно, от удельного объёма газа, который в свою очередь зависит от давления и температуры. В идеальных газах силы взаимодействия между молекулами отсутствуют и поэтому его внутренняя энергия равна кинетической (U = U_к) и зависит только от температуры. В технической термодинамике определяется не абсолютное значение внутренней энергии, а её изменение при переходе газа из одного состояния в другое. Поэтому за ноль можно принять любое её значение. Обычно принимают U = 0 при нормальных условиях:   = 0° С и   = 0,1 МПа.

С математической точки зрения дифференциал внутренней энергии представляет собой полный дифференциал, т.к. величина её измерения зависит только от начального и конечного состояния газа и  не зависит от процесса, т.е.

                                            ,                                             (1.15)

где    U₁ - внутренняя энергия газа в начальном состоянии;

         U₂ - внутренняя энергия газа в конечном состоянии.

В системе СИ внутренняя энергия измеряется в Дж. В термодинамических расчетах обычно используется удельная внутренняя энергия u, .    

Другим калорическим параметром, определяющим полную энергию системы, является энтальпия*. Энтальпия (I) представляет собой однозначную функцию термодинамической системы численно равную сумме внутренней энергии газа и произведению давления на объём, т.е.

                                                        I = U + pV                                       (1.16)

Как видно из выражения (1.16) размерность энтальпии равна размерности внутренней энергии, а в термодинамических расчётах используется удельная энтальпия i.

                                                        i =                                        (1.17)

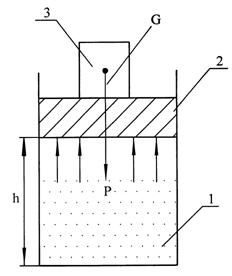
Для вывода уравнения (1.16) поместим газ давлением  p  в цилиндр площадью S под поршень, вес которого G (рис. 1.3).      

_________________

энтальпия* - «enthalpo» (нагреваю)

Необходимо отметить, что энтальпия газа зависит от его термических параметров и представляет собой одну из функций его состояния.

Третьим калорическим параметром состояния является энтропия S**, которая для изолированной термодинамической системы выражается отношением количества теплоты к абсолютной температуре, при которой теплота подводится к телу, или отводится от него:                                                                                                                                     (1.18)

Для бесконечно малого процесса уравнение (1.18) записывается в дифференциальной форме:

                                                                                                                (1.19)

Из уравнения (1.19) следует, что при подводе теплоты  dQ  к телу с постоянной температурой его энтропия  dS  возрастает, что свидетельствует о наличии теплообмена между рабочим телом и окружающей средой.