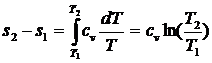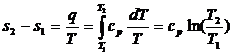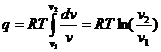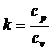2. Законы термодинамики

В основе термодинамики как науки лежат её первый и второй законы, устанавливающие качественные и количественные взаимосвязи  между теплотой и механической работой [2].

Первый закон термодинамики устанавливает количественную связь между теплотой и механической энергиями и представляет собой балансовое уравнение изменения энергии в термодинамической системе:

                              u2 - u1 = q – l+ a,                                           (2.1.)

где    (u2 – u1)  - изменение удельной внутренней энергии;

         q – удельная теплота c которой тело обменивается энергией с окру

               жающей средой;

         l – удельная работа по изменению объёма;    

         a – работа немеханического характера.

К работе немеханического характера можно отнести работу по переносу электрического заряда, работу (теплоту) химического взаимодействия и др.

Если считать, что a = 0, то u2 – u1= q – l. В математическом выражении первого закона термодинамики принято подводимую к телу теплоту выражать как функцию внутренней энергии и работы:

                              q =u2 - u1 + l,                                 (2.2)

Тогда первый закон термодинамики с учётом (2.2.) формулируется следующим образом:  вся подводимая к телу теплота идёт на изменение внутренней энергии и на совершение работы.

Отметим, что первый закон термодинамики, описывающий эквивалентное превращение теплоты и механической энергии, является частным случаем закона сохранения и превращения энергии, открытого М.В.Ломоносовым.

Из молекулярно-кинетической теории следует, что внутренняя энергия тела пропорциональна его температуре, тогда её изменение будет пропорционально разности температур, т.е.

                             U2 – U1 = cv (T2 – T1)                               (2.3)

Удельная работа расширения  l  в уравнении  (2.2.) совершается против внешних сил, например расширение газа в цилиндре при постоянном давлении, и  аналитически выражается следующим образом:

                                               l = p (v2 – v1),                                                 (2.4)

где  p – полное (абсолютное) давление газа, м3/кг.

С учётом уравнений (2.3) и (2.4) первый закон термодинамики можно представить в развёрнутом виде:                                     

                                       q = cv (T2 – T1)+ p (v2 – v1),                      (2.5)

Уравнение (2.5) часто используется при описании работы теплоэнергетических машин и установок, а так же для анализа типовых термодинамических процессов в газах, которые являются частными случаями первого закона термодинамики.

Теоретически измененные состояния газа полностью характеризуются тремя параметрами p, v и T, при этом теплота либо подводится к газу, либо отводится от него. Такие процессы называются политропными*. Наибольший практический интерес представляют такие процессы, в которых один из основных параметров остаётся постоянным, или процесс осуществляется без теплообмена с окружающей средой. Таких процессов в природе существует четыре:

- изохорный  (v = const);

- изобарный  (p = const);

- изотермический   (T = const);

- адиабатный  (dq = 0)

При исследовании термодинамических процессов обычно определяют:

- зависимости между изменяющимися параметрами газа;

- количество теплоты подводимой к рабочему телу;

- изменение внутренней энергии;

- работу расширения газа.

  

Все процессы при этом рассматриваются как равновесные и обратимые, а их исследование осуществляется на основе уравнения состояния идеального газа и первого закона термодинамики.

   Изохорный процесс – это равновесный процесс, протекающий при постоянном объёме (v=const). Такой процесс осуществляется, например, при нагревании или охлаждении газа в замкнутом объёме. Так как в изохорном процессе не происходит изменение объёма, то уравнение первого  закона термодинамики (2.5) при (v2 – v1) =0 будет иметь следующий вид:                 

                                              q = cv (T2 – T1), ,                                        (2.6)

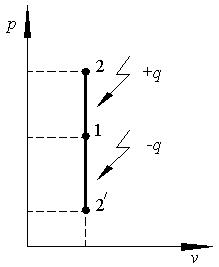
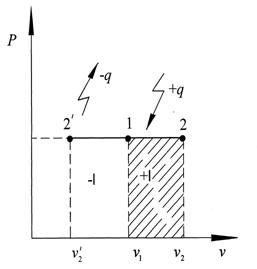
т.е. в изохорном процессе вся подводимая к телу теплота идёт на изменение его внутренней энергии.

Уравнение (2.6) определяет внутреннюю энергию 1кг газа в изохорном процессе, а его полная внутренняя энергия (m кг) определяется по уравнению(2.7):                           Q = cv m (T2 – T1), Дж                                      (2.7)

В p – v координатах изохорный процесс изображается вертикальным отрезком (рис.2.1).

                  

Рис. 2.1

На рис. 2.1 процесс изохорного нагревания 1–2, а изохорного охлаждения 1-21. Площадь под линией изохорного процесса равна нулю, что свидетельствует об отсутствии  работы.

Для  построения графика изохорного процесса в T–s  координатах используется выражение для энтропии:

                             ds=cv,                           (2.8)           

где dq = cvdT, тогда после интегрирования (2.8) в пределах температур от  T1 до T2 получим:

                  

______________

·        «поли» - много

                    

                                                                               (2.9)

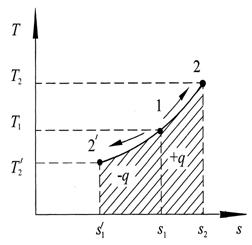
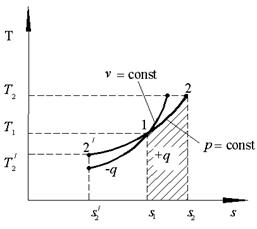
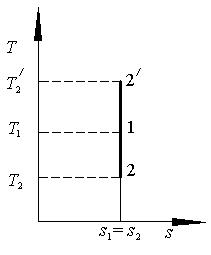
Как следует из выражения (2.9), линия изохорного процесса в T–S  координатах являются логарифмической кривой (рис 2.2).

 

 Рис. 2.2

В процессе 1 – 2 теплота подводится к рабочему телу и энтропия системы  возрастает. Процесс 1-21 идёт с отводом теплоты а энтропия при этом уменьшается.

Изобарный процесс – это равновесный процесс, протекающий при постоянном давлении.

В p – v координатах изобарный процесс (рис. 2.3) представляет собой

горизонтальный отрезок. На рис. 2.3 в процессе 1–2 теплота  q подводится к рабочему телу и совершается работа расширения.  Для изобарного процесса уравнение первого закона термодинамики (2.5)  применяется   в общем виде, но вместо изохорной теплоёмкости cv  используется изобарная, т.е. теплоёмкость при постоянном  давлении cp:

                                                                  (2.10)

Тогда можно заключить, что в изобарном процессе часть подводимой к телу теплоты переходит в его внутреннюю энергию, а другая часть превращается в работу расширения.

Для построения изобарного процесса в T-s  координатах подставим значение удельной теплоты q в общую формулу удельной энтропии для конечного процесса:   

                                                                 (2.11)           

 

 

 

                            Рис. 2.3

Из уравнения (2.11) следует, что изобара как и изохора  в T-S  координатах изображается логарифмической кривой (рис.2.4), но угол наклона изобары меньше угла наклона изохоры, т.к. в заданном диапазоне температур       cр> . Следовательно,  в одном  диапазоне температур увеличение энтропии в изобарном процессе происходит быстрее, чем в изохорном.

 

 

 

Рис. 2.4

Изотермический процесс – это равновесный процесс (рис.2.5),  протекающий при постоянной температуре(T=const).График изотермического процесса в p-v  координатах представляет собой равнобокую гиперболу, так как по закону Бойля-Мариотта при  T = const имеем pv = const. На практике такой процесс можно осуществить путём подвода или отвода теплоты,

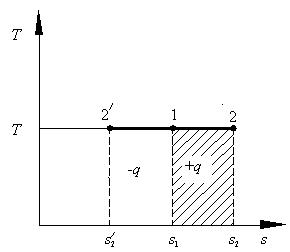
сопровождающегося сжатием или расширением газа, находящегося под поршнем в цилиндре с идеально теплопроводными  стенками. Очевидно, что в T – s  координатах изотерма представляет собой горизонтальный отрезок прямой  (рис.2.6), так как подвод и отвод теплоты   не  вызывает   изменения  температуры рабочего тела. В связи с тем, что при постоянной температуре внутренняя энергия тела не изменяется  (T2 – T1 = 0), то вся подводимая к телу теплота  расходуется  на  совершение работы.

Тогда первый закон термодинамики (2.1) будет иметь следующий вид:

                                                                                                 (2.12)    

  С учетом уравнения состояния идеального газа можно принять, тогда (2.12) можно записать следующим образом:

 

 

 

Рис. 2.5

                     (2.13)

Уравнения (2.13) на практике часто используется для вычисления работы изотермического процесса.

Адиабатный процесс – это такой равновесный процесс, который совершается без теплообмена с окружающей средой (dq=0). Для него уравнение первого  закона термодинамики в дифференциальной форме может быть представлено в следующем виде:

 

 Рис. 2.6

                              (2.14) Слагаемые в левой части этого уравнения представляют собой бесконечно малые величины изменения внутренней энергии и работы расширения. После замены переменных и интегрирования выражения (2.14) получим уравнение адиабаты в интегральной форме:

                                   (2.15)

                                         где  - показатель адиабаты

На рис. 2.7 линия адиабаты круче изотермы, а удельная работа расширения  l равна площади под кривой 1 – 2. Так как в адиабатном процессе подводимая теплота  q равна нулю, то для совершения работы расширения используется  часть внутренней энергии тела, т.е. . Аналитически удельную работу расширения адиабатного процесса принято выражать через  параметры p и v, как   изменение   удельной внутренней энергии с обратным знаком, т.е.:

                                                                                                        (2.16)

        Необходимо отметить, что наряду с изменением внутренней энергии работа адиабатного процесса зависит от показателя адиабаты k, значение которого для двух атомных газов равно 1,4.

Рис. 2.7

 

Рис. 2.8

            В T–s  координатах адиабата изображается вертикальной линией, т.к. из формулы для энтропии следует, что при dq = 0 измерение энтропии ds = 0 (рис. 2.8).

 В процессе  1– 21 происходит адиабатное сжатие, при котором температура тела повышается за счёт увеличения его      внутренней энергии. Процесс 1–2 сопровождается адиабатным расширением с понижением температуры за счёт уменьшения внутренней энергии рабочего тела. Практически процесс приближённый к адиабатному  осуществляется при быстром рас-

 

ширении (или сжатии) газа, находящегося под поршнем в цилиндре с изолированными от внешней среды стенками.  Анализ типовых термодинамических процессов позволяет сделать вывод о том, что все эти процессы являются частными случаями общего уравнения первого закона  термодинамики, а в уравнении изобарного процесса  вместо   изохорной теплоёмкости cv используется  изобарная  cp

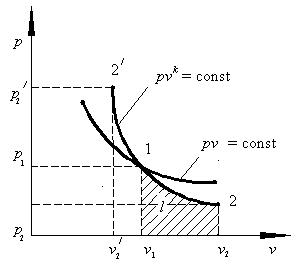
Сопоставляя уравнения четырёх рассмотренных процессов в p – v  координатах можно установить, что они описываются  произведением( p v)  и отличаются друг от друга показателем степени при  v :

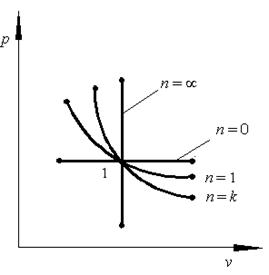
- изохорный процесс         (n =¥ ) ;

- изобарный процесс           p = const  (n = 0 ) ;

- изотермический процесс    p v  = const  (n =1 ) ;

- адиабатный процесс           p vk  = const  (n =k ).

         Тогда все эти процессы можно описать одним обобщающим уравнением (2.17):

                                               pvn = const,                                      (2.17)

Такой обобщающий процесс называется политропным, а n – показатель политропы.

         Для наглядного сопоставления исследуемых процессов изобразим на одном рисунке все четыре графика, проходящие через общую точку 1   

(рис. 2.9).

Рис. 2.9

 Очевидно, что через точку 1 можно провести бесконечное множество линий (процессов), называемых политропами, в пределах угла наклона ± ¥. Расчётные зависимости между параметрами состояния в любом политропном процессе аналогичны зависимостями, описывающим адиабатный процесс при n = k.