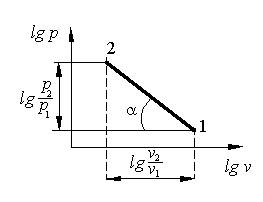
Наличие гиперболических кривых на графиках политропных процессов значительно увеличивает трудоёмкость теплотехнических расчётов и снижает  их точность. Поэтому, на практике  принято  представлять   политропные процессы в логарифмических координатах (lg p – lg v), где графики всех процессов – прямые линии.

Для представления политропных процессов в логарифмических координатах логарифмируем уравнение (2.17):

                                               lg p + n lg v= const                                     (2.18)

Уравнение (2.18) с привязкой к выбранной системе координат можно записать в более удобном виде:

                                                lg p= const -  n lg v,                                (2.19)

где  n –  показатель политропы. На  рис.2.10 видно, что графики термодинамических процессов в логарифмических  координатах  отличаются друг от

Рис. 2.10

друга значением угла α, а показатель политропного процесса  n = tg α. Как было отмечено ранее, первый закон термодинамики устанавливает количественную взаимосвязь между теплотой и механической энергиями, а  условий взаимного превращения этих видов энергий он не определяет. Эту задачу решает  второй закон термодинамики, который в дополнение к первому говорит о необратимости всех реальных процессов, об условиях превращения тепловой энергии в механическую и о направлении протекания того или иного процесса.

 Из опыта известно, что теплота самопроизвольно может переходить только от более нагретых тел к телам менее нагретым, т.е. самопроизвольный (естественный) теплообмен обладает свойством направленности. Однако, в  искусственных условиях возможен и обратный несамопроизвольный процесс: передача теплоты от менее нагретых тел к более нагретым. В этом случае для осуществления обратного процесса требуется подвести к телу внешнюю энергию. Примером такой энергетической установки может служить холодильник, в котором для осуществления обратного процесса используется электрическая энергия,  преобразуемая в механическую, а за тем во  внутреннюю энергию рабочего тела. Отмеченную особенность теплообмена впервые установил Р. Клаузис, который предложил первую формулировку второго закона термодинамики:

теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому, или некомпенсированный переход теплоты от тела с меньшей температурой к телу с большей температурой невозможен.

Отметим ещё одну особенность теплоты, которая состоит в том, что работа может полностью превратиться в теплоту (например, при трении), а для осуществления обратного процесса - превращения теплоты в работу, требуется какой-либо  дополнительный процесс, или компенсация. Так для получения работы из теплоты в тепловых двигателях требуется периодическое повторение процессов расширения – сжигания, что сопровождается возвращением тела в исходное состояние с затратой некоторой работы.

На рис. 2.11. представлен круговой процесс работы (цикл) поршневого теплового двигателя в координатах р – v.  В процессе (1- m – 2) при подводе теплоты q происходит расширение рабочего тела и совершается работа расширения . В обратном процессе (2-n-1) теплота   должна отводиться от рабочего тела в окружающую среду, на что затрачивается работа сжатия l2 равная площади . Полезная работа ( l0 = l1- l2 ) равна площади замкнутой кривой цикла.  

Рис. 2.11

             1 – цилиндр;

             2 - поршень

Следовательно, для обеспечения достаточно длительной работы двигателя необходимо осуществлять круговой процесс, в котором, наряду с подводом тепла q к рабочему телу от горячего источника необходимо отводить теплоту q2 к холодному источнику, т.е. необходимо иметь разность температур. Изложенные теоретические предпосылки позволили французскому инженеру Сади Карно предложить вторую формулировку второго закона термодинамики: для получения из теплоты работы необходимо иметь разность температур. Тепловой двигатель, работающий только с одним верхним (горячим) источником теплоты,

 

называется вечным двигателем второго рода. Тогда второй закон термодинамики можно сформулировать следующим образом: вечный двигатель второго рода невозможен.

 Действительно, если допустить существование теплового двигателя, который работал бы только за счёт охлаждения верхнего источника теплоты, то используя  запасы внутренней энергии атмосферы или воды океана можно было бы получить неограниченное количество «даровой» энергии, т.е. запустить в работу вечный двигатель. Теоретические запасы тепловой энергии в мировом океане практически неисчерпаемы. По ориентировочным расчётам установлено, что использование тепловой энергии воды океана для питания всех энергоустановок земного шара охладила бы океан на 0,01оС за 1700 лет. В современных тепловых машинах воздух атмосферы и вода океана используются только в качестве нижних (холодных) источников теплоты, а верхние источники создаются искусственно за счёт сгорания органического топлива или ядерной реакции.

С точки зрения теории вероятностей определённая направленность самопроизвольных процессов и их необратимость объясняется стремлением системы перейти от неравновесного состояния к равновесному, как более устойчивому и вероятному. Тепловая энергия, передаваемая в процессе теплообмена, обусловлена хаотичным движением частиц вещества, а механическая энергия представляет собой упорядоченное движение структурных частиц. Теоретически можно представить, что упорядоченное  движение может легко стать хаотическим как наиболее вероятным, а упорядочение хаотического движения связано с большими трудностями и затратой внешней энергии. Исходя из подобных теоретических предпосылок в 1872 году Людвиг Больцман  предложил ещё одну формулировку второго закона термодинамики, называемого принципом Больцмана: природные процессы стремятся перевести термодинамическую систему из состояний менее вероятных в состояния  более вероятные.

Аналитически принцип Больцмана имеет следующий вид:

                                               S = k ln W,                                                   (2.20)

где:   S –энтропия, ;

 

         k – постоянная Больцмана (k = 1,38·10-23 );

        W – термодинамическая вероятность.

В соответствии с принципом Больцмана любые термодинамические системы стремятся к равновесному состоянию, для которого S и W максимальны.

Основными техническими характеристиками любой тепловой машины являются её мощность и коэффициент полезного действия (КПД). Теоретических ограничений мощности  тепловых двигателей нет, а их КПД при заданных значениях температур верхнего и нижнего источников теплоты  ограничен. Для осуществления замкнутого процесса, в общем случае, следует

 

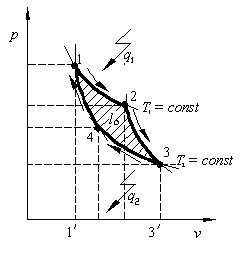
привести несколько прямых и обратных процессов. Отметим, что на проведение обратных процессов тепловые двигатели не получают работы от окружающей среды, а используют некоторую часть произведённой ими работы расширения. Следовательно, что бы двигатель работал, работа расширения  должна быть больше работы сжатия. На основе  анализа термодинамических циклов С. Карно предложил идеальный цикл тепловой машины, имеющий наибольший КПД. Этот цикл состоит из двух изотерм и двух адиабат (рис. 2.12).   Теплота q1  подводится по верхней  кривой   в  процессеизотермического расширения (1-2). Далее в процессе (2-3) происходит адиабатное расширение, при котором температура уменьшается от T1 до  T2. Обратные процессы (4-3) и (4-1) представляют собой изотермическое и адиабатное сжатие. Как следует из предыдущего цикла (рис. 2.11) полезная работа цикла Карно l0 будет равна площади (1,2,3,4). Для более наглядного анализа

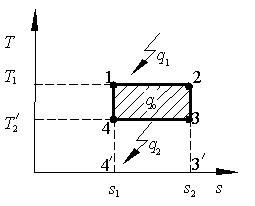
               Рис. 2.12                                               Рис. 2.13

КПД поcтроим цикл Карно в TS координатах (рис.2.13).Здесь: площадь (4´,1,2,3´) – подведённая теплота q1, площадь (4´,4,3,3´) – отведённая теплота q2  Тогда площадь цикла (1,2,3,4) – теплота qo , превращённая в полезную работу, т.е. qo =  q1- q2. Отметим, что на p-v диаграмме линия прямого процесса расширения (1,2,3) должна проходить выше линии обратного процесса сжатия (3,4,1) и чем меньше работа сжатия, тем более  экономично   работает двигатель. Основной характеристикой экономичности любого цикла тепловой машины принято считать термический КПД, который равен отношению теплоты превращённой в работу ко всей подведенной в цикле теплоте (2.21)

                                                                                                  (2.21)

где:     - термический КПД;

          q1  -   подведённая теплота;

                 q2 –  отведённая теплота.

С учетом формулы для определения энтропии термический КПД цикла можно выразить через  температуры верхнего T1  и нижнего T2 источников теплоты:                                                                          (2.22)        

Из формулы (2.22) следует, что термический КПД цикла Карно не зависит от природы рабочего тела, а является функцией температур верхнего и нижнего источников теплоты. Отметим, что цикл Карно имеет наибольший термический КПД, так как в T-S  координатах представляет собой прямоугольник, площадь которого в заданных диапазонах изменения энтропии и температуры будет больше площади любого другого цикла вписанного в этот прямоугольник.

Наряду с прямым циклом Карно существует и обратный цикл, в котором передача теплоты происходит от холодного источника к горячему путём затраты внешней энергии (холодильные установки). Степень совершенства обратного цикла Карно характеризуется холодильным коэффициентом , который равен отношению подведённой теплоты q2  к работе цикла  lo ( 2.23).

                                       =                                              (2.23)

         Циклы холодильных установок  рассмотрены в разделе 5.