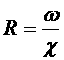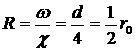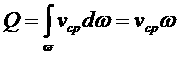|
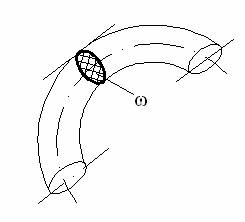
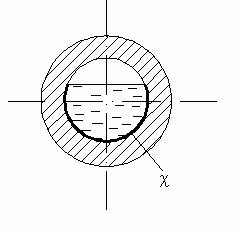
4. Основы гидродинамики Гидродинамика изучает законы движения жидкостей и взаимодействия их с соприкасающимися телами [4]. В теоретической гидродинамике принята струйная модель потока жидкости, где элементарная струйка представляет собой часть потока бесконечно малого сечения. Причём, скорость частиц жидкости в пределах сечения струйки одинакова. Для описания геометрии потока используются следующие кинематические элементы: -живое сечение; - смоченный периметр; - гидравлический радиус. Живое сечение ω - это поперечное сечение потока, нормальное ко всем линиям тока его пересекающим (рис. 4.1). Смоченный периметр c - линия, по которой жидкость соприкасается с поверхностями русла (рис. 4.2).
Отметим, что при напорном движении жидкости в трубе жидкость занимает весь внутренний объём и смоченный периметр равен геометрическому параметру трубы. Гидравлический радиус R – это отношение площади живого сечения к смоченному периметру, т.е.
При напорном движении
в круглой трубе
** Гидравлический радиус круглой трубы….. Основными гидравлическими характеристиками потока являются расход жидкости, средняя скорость и давление. Расход – это количество жидкости, протекающее через живое сечение потока в единицу времени. Количество жидкости может измеряться в различных физических величинах и в соответствии с ними расход может быть объёмный, массовый и весовой. Рассмотрим математические выражения различных видов расходов для элементарных струек: - объёмный расход dQ, м3/с:
dQ = где u - скорость жидкости в струйке. - массовый расход dM, кг/с:
dM =
где
- весовой расход dG, н/с:
dG =
В практических расчётах потоков жидкостей, часто используется объёмный расход Q , выражение для которого получим после интегрирования (4.2):
где
Одним из основных уравнений гидродинамики является уравнение неразрывности потока, которое связывает между собой скорости потока и площади живых сечений при условии постоянства расхода в различных сечениях [5]. Для несжимаемой жидкости это уравнение имеет следующий вид:
Уравнение (3.6) принято представлять в виде пропорции: νср1 / vcр2 = ω2 /ω1 (4.7) Из выражения (3.7) можно сделать вывод: скорости потока обратно пропорциональны площадям живых сечений. ** Вывод уравнения неразрывности потока …. Это уравнение часто используется при расчётах трубопроводов, состоящих из труб различных диаметров.
В случае движения сжимаемой жидкости (газа) при переходе от одного
сечения к другому её удельный вес
|