Алгоритмы построения оптимальной триангуляции
Как вы уже смогли заметить (рис. 2) задача построения триангуляции по исходному набору точек является неоднозначной, вследствие чего возникает вопрос, какая из двух различных триангуляции лучше? Одним из подходов к определению «лучшей» триангуляции может служить так называемая, оптимальная триангуляция, для которой сумма длин всех её рёбер минимальна среди всех возможных триангуляции, построенных на тех же исходных точках. Однако обосновано, что задача построения такой триангуляции является NP-полной. Поэтому для большинства реальных задач существующие алгоритмы построения оптимальной триангуляции неприемлемы ввиду слишком высокой трудоёмкости. При необходимости на практике применяют приближенные алгоритмы.
Вспомним:
- NP-полная задача- задача из класса NP, к которой можно снести любую другую задачу из класса NP за полиномиальное время.
- Класс задач NP включает в себя задачи, для решения которых существует недетерминированный алгоритм, полиномиальный по времени.
- Недетерминированный алгоритм – алгоритм, который указывает несколько путей обработки одних и тех же входных данных, без какого либо уточнения какой именно вариант будет выбран.
- Алгоритм полиномиальный по времени - алгоритм, трудоемкость которого порядка, т.е. время работы которого не слишком сильно зависит отразмера входных данных (не превосходит многочлена от размера данных). Таким образом
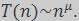
- Трудоемкостью (временной трудоемкостью, временной сложностью) алгоритма называется количество элементарных шагов, выполняемых алгоритмом для данного входа. Обозначается T(n).
- Элементарным шагом называется любое действие алгоритма, время выполнения которого не зависит от длины входа.
- Поскольку время выполнения каждого элементарного шага
не фиксировано, то математический смысл имеет не сама функция трудоемкости, а сё асимптотический порядок при n →∞
- На данный момент не известно полиномиальных алгоритмов для точного решения NP-трудных задач. Более того, специалисты по теории сложности склоняются к варианту, что таких алгоритмов не существует. Одним из подходов борьбы с NP-трудными задачами на практике является разработка приближенных алгоритмов.
Таким образом, раз задача построения оптимальной триангуляции является NP-полной, то не существует точного алгоритма её* решения.