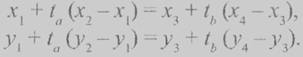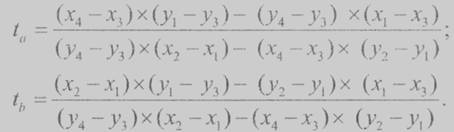Жадный алгоритм построения триангуляции

   

    Одним из первых точных алгоритмов был предложен так называемый жадный алгоритм построения триангуляции. Суть данного алгоритма:
    Шаг 1. Генерируется список всех возможных отрезков, соединя­ющих пары исходных точек, и он сортируется по длинам отрезков.
    Шаг 2. Начиная с самого короткого, последовательно выполняет­ся вставка отрезков в триангуляцию. Если отрезок не пересекается с другими ранее вставленными отрезками, то он вставляется, иначе он отбрасывается.
    Трудоемкость работы жадного алгоритма при некоторых его улучшениях составляет 0(n² log n). В связи со столь большой трудо­емкостью на практике он почти не применяется. Однако благодаря возможностям современной компьютерной техники, особенно при небольших входах, его можно реализовать.
     Мы реализовали данный алгоритм на практике. При этом мы ис­пользовали: сортировку точек по абсциссе, прием нахождения наи­меньшего элемента для сортировки отрезков по их длинам, а также нахождение пересечения отрезков на плоскости.
      Что касается сортировки, то можно использовать любую из из­вестных Вам сортировок массивов (см. [17]). В нашей практической реализации мы воспользовались, так называемой, быстрой сортиров­кой Хоара, которую использовали и ранее (см. [5]).
    Сортировка отрезков, соединяющих пары исходных точек, по длинам была реализована на основе стандартной схемы нахождения наименьшего элемента: полагали первый элемент массива наимень­шим, если в оставшейся части массива находился элемент меньше данного, то он менялся с наименьшим, таким же образом искались последующие наименьшие по длине отрезки в оставшейся не отсо­ртированной части массива.
    Для определения наличия пересечения отрезков мы воспользова­лись знаниями из геометрии (см. [4]). Путь на плоскости заданы два отрезка а и b, а - точками с координатами (х₁, у₁) и (х₂, y₂), а b – точка­ми с координатами (х₃,у₃) и (х₄, y₄). Необходимо найти их точку пере­сечения с координатами (х, у). Уравнение прямой, на которой лежит отрезок a имеет вид:

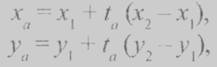
где (х_а, у_а) - координаты любой точки отрезка а; t_a - параметр, прини­мающий значения [0,1].
      Аналогично для отрезка b имеем:

где (х_b, у_b) координаты любой точки отрезка b; t_b - параметр, прини­мающий значения [0,1].
   Таким образом, если отрезки пересекаются в какой-либо точке, то соответствующие координаты этой точки должны удовлетворять уравнениям:

      Решения систему из последних двух уравнений относительно t_а и t_b, получим:

      Подстановка любого из этих значений в соответствующее уравне­ние прямой даёт точку пересечения.
      Замечания:
      - Знаменатели одинаковы.
      - Если знаменатель равен нулю, то прямые параллельны.
      - Если и числитель и знаменатель равны нулю, то прямые совпадают.
      - Если нужно найти пересечение отрезков, то нужно лишь проверить, лежат ли t_а и t_b на промежутке [0,1]. Если какая – нибудь из этих двух переменных принимает значения из проме­жутка [0,1], то соответствующий отрезок содержит точку пересе­чения. Если обе переменные приняли значения из [0,1], то точка пересечения прямых лежит внутри обоих отрезков. Причем что­бы исключить проверку совпадения концов отрезков (так как они у нас будут совпадать, например, может быть ребро (1, 2) и ребро (2, 3)), достаточно рассматривать интервал (0,1).
      -Для двух отрезков при достаточной разреженности объ­ектов можно сначала проверять принципиальную возмож­ность пересечения, сравнивая координаты концов.
      Весь необходимый теоретический материал для практической ре­ализации построения жадной триангуляции изложен. Программа го­това и приведена ниже в виде кода программы решения поставлен­ной задачи.
    Перед Вами ставится задача написать рецензию на изложенный алгоритм построения жадной триангуляции.
    Напомним, что рецензия - это изложение анализа текста, в котором рассматриваются его содержание и форма, отмечаются и аргументи­руются его достоинства и недостатки, делаются выводы и обобщения.
    То есть ваша рецензия должна содержать анализ текста програм­мы с отмеченными и аргументированными его достоинствами и не­достатками, сделанными выводами и обобщениями. Можно, напри­мер, начать рецензию с ответов на следующие вопросы. Является ли данная программа работоспособной (содержит ли существен­ные ошибки)? Все ли шаги предлагаемой программы Вам понятны? Является ли данная реализация эффективной с точки зрения техники программирования, можно ли предложить способы улучшения качества кода? и т.п.
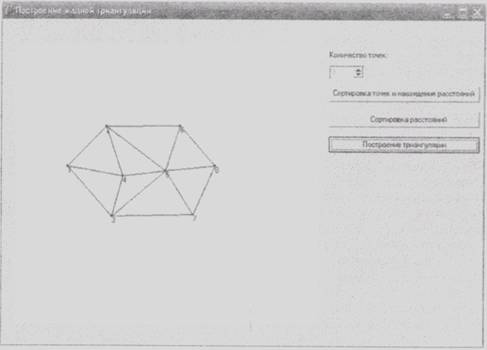
    Визуально форма для демонстрации процесса построения жадной триангуляции выглядит так, как показано на рис. 3.
      В табл. 1 приведен листинг программы построения триангуляции с помощью жадного алгоритма и подробное описание отдельных ша­гов алгоритма.

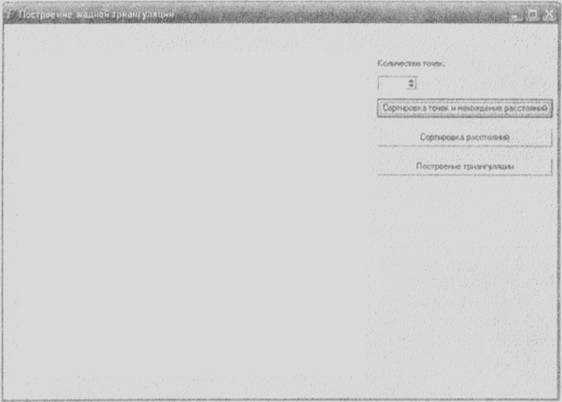
Рис. 3. Вид формы для демонстрации процесса построения триангуляции с помощью жадного алгоритма

 

Листинг модуля формы и комментарии для программы построения жадной триангуляция Жми сюда

    Как Вы считаете, исходя из вышеприведенного определения за­дачи построения триангуляции, полученный ответ (рис. 4) нас удов­летворяет?

Рис. 4.Вид формы с результатом построение триангуляции с помощью жадного алгоритма

     Действительно - да, однако с точки зрения практики (например, для получения триангуляции Делоне из уже имеющейся триангуля­ции или построение линий уровня (изолиний) по триангуляции), три­ангуляцию необходимо рассматривать как нахождение множества треугольников, покрывающих все заданные точки множества и построение структуры данных, содержащей информацию об отношении соседства между треугольниками.