Алгоритм построения триангуляции со структурами triang1 и triang2

   Прежде чем рассматривать применяемые на практике алгоритмы триангуляции необходимо уточнить определение триангуляции.
   Триангуляция это нахождение множества треугольников, покрывающих все заданные точки множества (т.е. все точки являются вершинами треугольника) и построение структуры данных, содержащей информацию об отношении соседства между треугольниками. Таким образом, с практической точки зрения для построения триангуляции необходимо сформировать структуры: triang1, хранящую информацию о вершинах треугольников, входящих в триангуляцию, и triang2   об отношении соседства треугольников.
   Пусть дано некоторое множество точек М. Мощность данного множества точек М равна: |M| = n. Нам необходимо выполнить построение треугольников так, чтобы выполнялись следующие условия:
   1. Любая точка из множества М является вершиной треугольника. То есть для любой точки m_i I M. существует треугольник m_i такой, что точка m_i является вершиной треугольника T_j.
   2. Для любых двух треугольников T_j, T_k выполняется условие:

   То есть T_j «не накладывается» на T_k.

  = ВО, где ВО - выпуклая оболочка множества М.

   3. Для любого треугольника T_j определенны треугольники T_j1, T_j2, T_j3, которые являются соответственно соседями к треугольнику T_j по любой стороне (T_jk = 0, если соответствующие стороны внешние).
   4. Постарайтесь проанализировать рассуждения построения триан­гуляции со структурами triang1  и triang2 с помощью языка програм­мирования Object Pascal но средствам ответов на следующие вопросы:
    - Можно ли использовать для хранения координат проставляю­щихся точек массив pts, каждый элемент которого является записью с двумя полями х и у, содержащими соответствующие координаты данных точек?
    - Можно ли применить быструю сортировку Хоара для располо­жения в порядке возрастания по координате х точки массива pts?
    - Можно ли сначала построить выпуклую оболочку данных точек, затем найти точку, ближайшую к «центральной» точке и произвести первоначальное построение триангуляции по этой точке и крайним? Далее определить те треугольники триангуляции, внутрь которых попадают оставшиеся точки исходных точек, не попавшие в триангуляцию, включить их в триангуляцию, перестроив нужным образом соответствующие структуры триангуляции.
    - Можно ли организовать массив triang1 множества треугольников, покрывающего заданные точки, следующим образом:
    triang1 [(x₁,y₁), (x₂,y₂), (x₃,y₃)] - любой треугольник задаётся тремя вершинами, каждая из которых имеет координаты: (х, у) в массиве pts (в самом массиве triang1 содержатся не координаты точек, а их индексы в массиве pts).
    - Можно ли организовать массив triang2 - массив структуры данных, содержащей информацию об отношении соседства между тре­угольниками, следующим образом:
      Triang2 [T₁,T₂,T₃] - каждый треугольник связан отношением соседства с тремя прилегающими к его сторонам треугольникам, причем T_j = 0, если соответствующие стороны внешние.
      При ответах на некоторые из поставленных вопросов вам могут помочь следующие теоретические позиции.
      Для построения выпуклой оболочки множества данных точек можно использовать уже вам известные алгоритмы построения выпуклой оболочки (см. [5]). Или воспользоваться следующей схемой: выпуклую оболочку представить условно состоящей из двух частей «верхней» и «нижней». Начинаем построение с верхней границы.
      В результате сортировки самая «левая» точка (с наименьшей координатой х) находится на первой позиции в массиве, а самая «правая» точка (с максимальной координатой х) на самом последнем месте.
   Полагаем первую точку текущей и вычисляем самый «левый» из векторов, направленных к другим точкам множества. Для этого нахо­дим синусы углов, образованные этими векторами по формуле:

   И выбираем вектор, максимальный по синусу.
   Точка, в которую направлен данный вектор, включается в оболочку вслед за текущей точкой. Далее, новую точку полагаем текущей, и для нее опять ищем самый «левый» вектор, при этом рассматриваются только точку с большим значением координаты (рис. 5). Процесс продолжается до тех пор, пока текущей не станет крайняя правая точка.

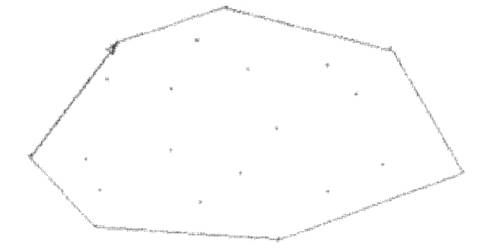
Рис 5. Самый левый вектор

   Алгоритм построения верхней части выпуклой оболочки можно представить следующим образом:
cur:=t;                                                              // Текущая точка (самая левая)
Image1.Canvas.MoveTo(pts[1].x, pts[1].y);       // Начинаем рисование с первой точки
white (cur<>n) do begin
max:=cur+1;
dy:=pts[cur].y-pts[cur+1].y;
dx:=pts[cur+1 ].x-pts[cur].x;
sinmax:=dy/sqrt(sqr(dx)+sqr(dy));
for j:=cur+2 to n do begin                                // Поиск самого левого вектора
dy:=pts[cur].y-pts[j].y;
dx:=pts[ j ].x-pts[cur].x;
sinj:=dy/sqrt(sqr(dx)+sqr(dy));
if sinj>sinmax then begin
max:=j;
sinmax:=sinj
end
end;
Image1.Canvas.
LineTo(pts[max].x,pts [max] .y);                     // Линия из текущей точки в указанную
Metki[max]:=false;                                          // Отмечаем точку, имеющую макси-
isVerh[max]:-true;                                           мальное значение синуса угла как про-
смотренную и попавшую в верхнюю 
часть выпуклой оболочки
cur:=max                                                     // Продолжить поиск с найденной точки
end;

      После этого аналогично строим «нижнюю» часть оболочки. Как вы думаете, какой угол надо рассматривать при этом, и как будет вы­глядеть алгоритм для данной подзадачи?
      Далее начинаем построение триангуляции выпуклой оболочки с нахождения центральной точки из всего множества точек, попав­ших в выпуклую оболочку, но не являющихся крайними. Для отслеживания принадлежности исходных точек к вершинам выпуклой оболочки в ходе ее построения в программе их необходимо условно «пометить». В качестве центральной точки выбираем точку, которая удовлетворяет следующим условиям:
    - Точка не является «помеченной».
    - Это должна быть точка, которая находиться как можно ближе к центру выпуклой фигуры.
      Отсюда вытекает очевидный алгоритм поиска данной точки:
    1. Ищем координаты центра выпуклой фигуры (для этого доста­точно найти среднее арифметическое всех точек).
    2. Из всех непомеченных точек ищем ту, у которой минимально расстояние до центра.

      Замечание.  На самом деле, алгоритм будет работать, т.е. вычислять одну из триангуляции, и в случае, если централь­ная точка будет выбрана произвольным образом среди непоме­ченных. Однако в этом случае чаще будет наблюдаться эффект «вытянутых» треугольников, что отрицательно скажется на эффективности решения большинства прикладных задач с помощью данной триангуляции.
      На практике, для экономии времени, можно воспользоваться упо­рядоченностью массива pts по координате х. Тогда, пробуем выбрать медиану массива по координате х (в силу упорядоченности - элемент на средней позиции), если соответствующая точка помечена, то про­буем соседние по координате х к ней точки, если и они помечены, то соседние по координате х к ним и т.д.
      С помощью найденной центральной точки можно построить пер­воначальное множество треугольников: соединяем все точки, кото­рые являются вершинами выпуклой оболочки с центральной точкой (рис. 6).
      Данное множество необходимо описать с использованием струк­тур triang1 и triang2. Для формирования данных структур приведем пример построения триангуляции в ЭВМ. На рис. 7 изображена триангуляция выпуклой оболочки.

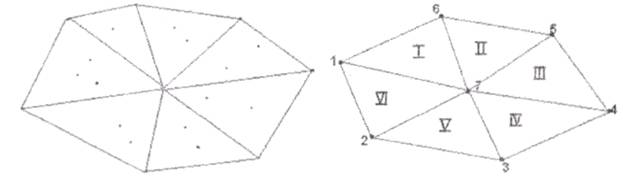
Рис. 6. Нахождение центральной точки                            Рис. 7. Пример триангуляции

      Соответствующие массивы: triang1 и triang2 заполняются следу­ющим образом:
      triang1 [(x₁,y₁), (x₂,y₂), (x₃,y₃)] - любой треугольник задаётся тремя вершинами, каждая из которых имеет координаты: (x, y) в массиве pts (в самом массиве triang1 содержатся не координаты точек, а их индексы в массиве pts);
      triang2 [T₁,T₂,T₃] - каждый треугольник связан отношением соседства с тремя прилегающими к его сторонам треугольникам.
      Тогда триангуляция выпуклой оболочки для конкретного примера в ЭВМ решается следующим образом:

	Triang1	triang2
t	(1,6,7)	(2,6,0)
2	(6,5,7)	(3,1,0)
3	(5,4,7)	(4,2,0)
4	(4,3,7)	(5,3,0)
5	(3,2,7)	(6,4,0)
6	(2,1,7)	(1,5,0)

   Таким образом, в первой строке в скобках (1,6,7) описывается треугольник I, который заключен между 1, 6 и 7 вершинами.    Далее во вторых скобках (2,6,0) для этого треугольника указывается отношение соседства: со стороны, заключённой между 6 и 7 вершинами (расположенной напротив 1-й вершины) треугольник I граничит с треугольником II. Со стороны, заключённой между 1 и 7 вершинами (напротив 6-й), треугольник I связан отношением соседства с тре­угольником пол номером VI. А со стороны, находящейся между точ­ками 1 и 6 (напротив 7-й вершины) соседнего треугольника нет, так как это внешняя сторона, поэтому в triang2 содержится 0. Следует заметить, что расположение вершин в triang1 может быть выбрано произвольно, однако построение triang2 напрямую зависит от triang1. Аналогично представляются остальные треугольники и их соседи.
   Таким образом, в результате предыдущих действий мы построи­ли первоначальную триангуляцию с использованием крайних точек выпуклой оболочки и центральной точки (рис. 6). При этом остались точки, которые попали в выпуклую оболочку, но не являются, ни вершинами выпуклой оболочки, ни центральной точкой. Данные точки надо включить и уже имеющуюся триангуляцию. Для этого необхо­димо для каждой i-й точки, пока не являющейся вершиной ни одною треугольника выполнить следующие действия:
      1. Найти треугольник, в который попадает i-я точка.
      Для решения данной задачи необходимо обеспечить перебор всех треугольников, и проверять на вхождение точки в каждый из них. Это легко реализовать с помощью векторного произведения (рис. 8, 9).

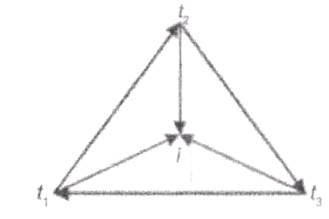
Рис. 8. Проверка точки на вхождение в треугольник

      При этом точка лежит внутри треугольника, тогда и только тогда, когда все знаки векторных произведений , , совпадают.
      2. Найденный треугольник, внутри которого лежит точка, следует разбить на 3 части, используя внутреннюю точку i, т.е. перестроить массив треугольников triang1 и массив соседства triang2.
      Итак, следующим этапом изучения алгоритма построения триан­гуляции со структурами triang1 и triang2 является практическая реализация данного алгоритма. В табл. 2 приведен листинг каркаса про­граммы, комментарии и методические рекомендации для реализации данного проекта. Конечный вариант вида формы может иметь следу­ющий вид (рис. 10).

 

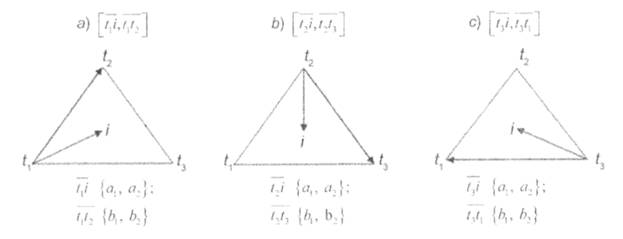
Рис. 9. Векторные произведения, необходимые для проверки на принадлежность точки треугольнику

Рис. 10. Вил формы построения триангуляции со структурами triang1 и triang2

 

      Вам необходимо заполнить пропуски в соответствии с рекомен­дациями, приведенными в качестве комментариев непосредственно в программном продукте и в методических рекомендациях. Вы може­те использовать предыдущий программный продукт, а также ранее вами изученные и реализованные на практике (см. [5]).    

      Таблица 2.
Листинг модуля формы, комментарии и методические рекомендации программы построения триангуляции со структурами triang1 и triang2  

Нажми сюда