Построение ломанной минимальной длины

     Если необходимо уменьшить осцилляцию изолинии и сократить число используемых для ее построения узловых точек, причем гладкости линии не требуется, то в качестве наиболее подходящей можно выбрать ломаную минимальной длины с заданными начальной и конечной точками. Эта ломаная но форме подобна резиновой нити с двумя закрепленными   концами, растянутой внутри коридора. Для построения ломаной минимальной длины внутри коридора предлагается следующий алгоритм. Пусть L₁, L₂, ... L_n – вершины левой гра­ницы, R₁, R₂, ...R_n,– вершины правой границы, точка М – текущая вершина минимальной ломаной. Начальная текущая точка М – это центр отрезка L₁R₁, а лучи ML₁, и MR₁, определяют начальный сектор видимости из текущей точки. При переходе к следующим нарам вершин (L₂ и R₂, L₃ и R₃, и т.д., см. рис. 20) сектор видимости может только уменьшаться, т.е. его правый луч может повернуться только влево, а левый – только вправо.
     В процессе проверки нар необходимо запоминать вершины L_mr и R_ml через которые проходят лучи МL_mr и МR_ml, являющиеся границами текущего сектора видимости, так как следующей текущей точкой станет либо L_mr, либо R_ml. Пусть при проверке вершин L_k и R_k, k > ml,k >mr, в результате очередного поворота луч МR_k оказался левее луча МL_mr (MR₅ левее ML₃ на рис. 20). Это означает, что левая граница закрывает весь отрезок L_kR_k (L₅R₅, на рис. 20) и необходимо перейти к новой текущей точке. В качестве нес выбирается вершина левой границы L_mr(точка L₃ на рис. 20). Новый начальный сектор образуют лучи L_mrL_mr+1 и L_mrR_mr (L₃L₄ и L₃R₃ на рис. 20), при этом последующая проверка начинается с пары mr + 1. При повороте коридора вправо картина симметрична. Процесс завершается, когда из текущей вершины будет видна конечная точка ломаной (если изолиния замкнутая, то начальная точка минимальной ломаной совпадает с конечной).

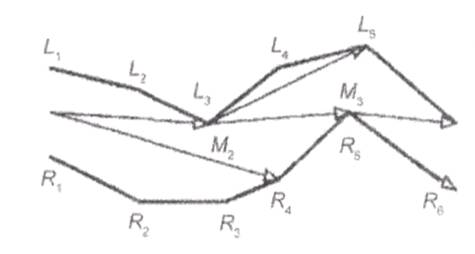
Рис. 20. Построение ломаной минимальной длины

     Легко показать, что каждая текущая вершина будет принадлежать ломаной минимальной длины: замена ее на любую другую точку отрезка, соединяющего чару вершин левой и правой границ коридора, может только удлинить ломаную.
     Трудоемкость алгоритма определяется числом вершин ломаной и числом проверок чар вершин коридора в каждой вершине ломаной. Эти две величины обычно зависят от ширины коридора: при ее уменьшении сужается сектор видимости, поэтому число вершин ломаной увеличивается, а число проверок пар уменьшается.
     Отметим, что построение ломаной минимальной длины можно производить прямо в процессе отслеживания границ коридора.