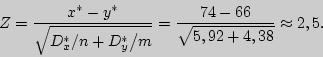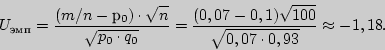Раздел 5. Проблема статистического вывода

 

Статистические гипотезы

На разных этапах статистического исследования возникает необходимость в формулировании и экспериментальной проверке некоторых предположительных утверждений (гипотез).Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Выдвигается основная (нулевая) гипотеза $Н_{0}$ и проверяется, не противоречит ли она имеющимся эмпирическим данным. Конкурирующей (альтернативной) называют гипотезу $Н_{1}$, которая противоречит нулевой.

В результате статистической проверки гипотезы могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза; вероятность совершить такую ошибку обозначают $\alpha $ и называют ее уровнем значимости. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза, вероятность которой обозначают $\beta $, а мощностью критерия является вероятность $1- \beta $.

Процедура обоснованного сопоставления высказанной гипотезы с имеющейся выборкой осуществляется с помощью того или иного статистического критерия и называется статистической проверкой гипотез. Под критической областью понимают совокупность значений критерия, при которых нулевую гипотезу $Н_{0}$ отвергают. Критическую область при заданном уровне значимости следует строить так, чтобы мощность критерия была максимальной.

Статистические критерии проверки гипотез разнообразны, но у них единая логическая схема построения, которую представим на рис. 103.

\includegraphics{D:/html/work/link1/metod/met12/ris103.eps}

1. Сравнение двух дисперсий нормальных генеральных совокупностей. При заданном уровне значимости $\alpha $ проверяется нулевая гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: 

\begin{displaymath}Н_{0}=D[X] = D[Y].\end{displaymath}

В качестве критерия проверки нулевой гипотезы принимают случайную величину отношения большей исправленной дисперсии к меньшей 

 

\begin{displaymath}F=S_{б}^{2} \quad / S_{м}^{2}.\end{displaymath}


Величина $F$ имеет распределение Фишера-Снедекора, которое зависит только от чисел степеней свободы $k_{1}=n_{1} - 1$ и $k_{2}=n_{2}- 1$.

Пример 1. Исследование длительности оборотных средств двух групп предприятий (по 13 предприятий в каждой) дало следующие результаты:

$х^{\ast } = 23$ дня, $у^{\ast }= 26$ дней, $\sigma _x^2 = 3$ дня, $\sigma _y^2 = 6$ дней.

Можно ли считать, что отклонения в длительности оборота оборотных средств групп предприятий одинаковы для уровня значимости 0,1?

Решение. В этой задаче надо проверить нулевую гипотезу $Н_{0} : D[X] = D[Y]$ о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе$Н_{1} : D[X] \ne \quad D[Y]$. Используем критерий Фишера-Снедекора со степенями свободы $k_{1}=k_{2} = 13 - 1$ и вычислим наблюдаемое значение критерия (отношение большей дисперсии к меньшей)

 

\begin{displaymath} F_{эмп} = {S_{б}^2 } \mathord{\left/ {\vphantom {{S_{б}^2 } ... .../ {\vphantom {6 3}} \right. \kern-\nulldelimiterspace} 3} = 2. \end{displaymath}

По таблице приложения 6 по уровню значимости для двусторонней критической области $\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-\nulldelimiterspace... ...athord{\left/ {\vphantom {{0,1} 2}} \right. \kern-\nulldelimiterspace} 2 = 0,05$ и числам степеней свободы $k_{1}=k_{2} = 12$ находим критическую точку

\begin{displaymath}F_{кр} (0,05; 12; 12) = 2,69.\end{displaymath}


Так как $F_{эмп}= 2 < 2,69 = F_{кр}$, то нет оснований отвергать нулевую гипотезу о равенстве отклонений в длительности оборота оборотных средств двух групп предприятий.

Пример 2. Школьникам давались обычные арифметические задачи, а потом одной случайно выбранной половине учащихся сообщалось, что они не выдержали испытания, а остальным - обратное. Затем у каждого из них спрашивали, сколько секунд ему потребуется для решения новой задачи. Экспериментатор, вычисляя разность между определенным временем решения задачи, которое называл школьник, и результатами ранее выполненного задания, получил следующие данные:

группа 1 (учащиеся, которым сообщалось о положительном результате)

$n_{1} = 13, S_1^2 = 4,06$

группа 2 (учащиеся, которым сообщалось о неудаче)

$n_{2}= 12, S_2^2 = 20,25$

Проверьте на уровне значимости 0,01 гипотезу о том, что дисперсия совокупности детских оценок, имеющих отношение к оценке их возможностей, не зависит от того, что сообщалось детям о плохих результатах испытаний или об удачном решении первой задачи.

Решение. Применим критерий Фишера-Снедекора для нулевой гипотезы $Н_{0} : D[X] = D[Y]$ и конкурирующей $Н_{1} : D[Y] > D[X]$. Вычислим наблюдаемое значение критерия

\begin{displaymath} F_{{\rm эмп}} = {S_2^2 } \mathord{\left/ {\vphantom {{S_2^2 ... ...,06}}} \right. \kern-\nulldelimiterspace} {4,06} \approx 4,99. \end{displaymath}

 

Критическую точку находим в приложении для уровня значимости $\alpha = 0,01$ и числам степеней свободы $k_{1} = 12 - 1$ и $k_{2} = 13 - 1$:

\begin{displaymath}F_{кр}(0,01; 11; 12) = 4,22.\end{displaymath}


Получили, что $F_{эмп} = 4,99 > 4,22 = F_{кр}$ и нулевая гипотеза на уровне значимости 0,01 отвергается.

2. Сравнение двух средних нормальных генеральных совокупностей с известными дисперсиями. Проверяется нулевая гипотеза о равенстве генеральных средних рассматриваемых совокупностей с заданными или вычисляемыми дисперсиями. В качестве критерия проверки нулевой гипотезы примем случайную величину

\begin{displaymath} Z = {\displaystyle x^\ast - y^\ast \over\displaystyle \sqrt ... ...ft/ {\vphantom {] m}} \right. \kern-\nulldelimiterspace} m} }. \end{displaymath}

Пример 3. Производительность двух моторных заводов, выпускающих дизельные двигатели, характеризуется следующими данными:

1-й завод

72

84

69

74

82

67

75

86

68

61

2-й завод

55

65

73

66

58

71

77

68

68

59

Можно ли считать одинаковыми производительности дизельных двигателей на обоих заводах при уровне значимости $\alpha =0,05$?

Решение. Найдем выборочные числовые характеристики данных независимых выборок:

\begin{displaymath}х^{\ast } = 74, D_x^\ast = 59,2, y^{\ast } = 66, D_y^\ast = 43,8.\end{displaymath}


Найдем наблюдаемое значение критерия:

\begin{displaymath} Z_{{\rm эмп}} = {\displaystyle x^\ast - y^\ast \over\display... ...e 74 - 66\over\displaystyle \sqrt {5,92 + 4,38} } \approx 2,5. \end{displaymath}

 

По условию, конкурирующая гипотеза имеет вид $M[X] \ne M[Y]$, поэтому критическая область - двусторонняя.

Найдем критическую точку:

\begin{displaymath} \Phi (Z_{{\rm кр}} ) = {(1 - \alpha )} \mathord{\left/ {\vph... ...{(1 - 0,05)} 2}} \right. \kern-\nulldelimiterspace} 2 = 0,475, \end{displaymath}

по таблице функции Лапласа (прил. 2) находим $Z_{кр} \approx 2$.

Так как $\left\vert {Z_{эмп} } \right\vert = 2,5 > 2 = Z_{кр}$, то нулевая гипотеза об одинаковости производительности двух заводов отклоняется.

3. Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности. По выборочной средней при заданном уровне значимости проверяется нулевая гипотеза $Н_{0}: a = a_{0}$ о равенстве генеральной средней $a $ гипотетическому значению $a_{0}$. В качестве проверки нулевой гипотезы примем случайную величину

\begin{displaymath} U = (\bar {X} - {a_0 )} \mathord{\left/ {\vphantom {{a_0 )} ... ...sqrt n } \sigma }} \right. \kern-\nulldelimiterspace} \sigma , \end{displaymath}

которая распределена нормально.

Пример 4. Из нормальной генеральной совокупности с известным средним квадратическим отклонением $\sigma = 0,2$ извлечена выборка объема $n = 25$ и по ней найдена выборочная средняя $х^{\ast} = 21,04$. Проверить нулевую гипотезу $Н_{0}: a= a_{0} = 21$, при конкурирующей гипотезе $Н_{1}: а \ne 21$ и уровне значимости 0,1.

Решение. Найдем наблюдаемое значение критерия:

\begin{displaymath} U_{{\rm эмп}} = (х^\ast - а_0 ){\sqrt п } \mathord{\left/ {\... ...t {25} } {0,2}}} \right. \kern-\nulldelimiterspace} {0,2} = 1. \end{displaymath}

Найдем критическую точку двусторонней критической области:

\begin{displaymath} \Phi (U_{{\rm кр}} ) = (1 - {\alpha )} \mathord{\left/ {\vph... ...hantom {{0,1)} 2}} \right. \kern-\nulldelimiterspace} 2 = 0,45 \end{displaymath}

и по таблице функции Лапласа находим $U_{кр} \quad \approx 1,65$.

Поскольку $U_{кр} = 1,65 > 1 = U_{эмп}$, то нулевая гипотеза принимается.

4. Сравнение наблюдаемой относительной частоты с гипотетической вероятностью появления события. При заданном уровне значимости $\alpha $ проверяется нулевая гипотеза, состоящая в том, что неизвестная вероятность $р$ появления события равна гипотетической вероятности $р_{0}$ серии повторных независимых испытаний.

В качестве критерия проверки нулевой гипотезы принимаем случайную величину

\begin{displaymath} U = {\left( {{\displaystyle m\over\displaystyle n} - p_0 } \... ... } }}} \right. \kern-\nulldelimiterspace} {\sqrt {p_0 q_0 } }. \end{displaymath}

Пример 5. По 100 независимым испытаниям найдена относительная частота 0,07. При уровне значимости 0,05 проверить нулевую гипотезу $Н_{0 }: р= р_{0} = 0,1$ при конкурирующей гипотезе $Н_{1 }: р \quad \ne 0,1$.

Решение. Найдем наблюдаемое значение критерия:

\begin{displaymath} U_{эмп} = {\displaystyle \left( {m \mathord{\left/ {\vphanto... ...} \over\displaystyle \sqrt {0,07 \cdot 0,93} } \approx - 1,18. \end{displaymath}

Учитывая, что критическая область двусторонняя, находим $U_{кр}$ из равенства

\begin{displaymath} \Phi (U_{кр}) = (1 - {\alpha )} \mathord{\left/ {\vphantom {... ...tom {{0,05)} 2}} \right. \kern-\nulldelimiterspace} 2 = 0,475. \end{displaymath}

По таблице функции Лапласа (прил. 2) находим $U_{кр} \quad \approx 2$.

Поскольку $\left\vert {U_{эмп}} \right\vert = 1,18 < 2 = U_{кр} $, то нет оснований отвергать гипотезу о незначительном отличии наблюдаемой относительной частоты от гипотетической вероятности.

Вопросы для самоконтроля

  1. Назовите основные типы статистических критериев проверки гипотез.
  2. Что означает уровень значимости критерия?
  3. Что общего в методике построения доверительных интервалов и проверки статистических гипотез?
  4. Поясните смысл понятий "ошибка первого рода", "ошибка второго рода", "мощность критерия".
  5. В чем отличие одностороннего и двухстороннего критериев, простой и сложной гипотез?
  6. Как зависят области принятия основной гипотезы от уровня значимости?
  7. Как определяются критические границы для одностороннего и двухстороннего критериев при заданном уровне значимости?
  8. Приведите примеры практических задач по проверке гипотез о равенстве математических ожиданий, дисперсий.

Задачи

 По двум независимым выборкам, объемы которых $n_{1} = 10$ и $n_{2} = 15$, извлеченным из нормальных генеральных совокупностей $Х$ и $Y$, найдены исправленные выборочные дисперсии $S_{x} = 0,54$ и $S_{y} = 0,32$. При уровне значимости $\alpha = 0,1$ проверьте нулевую гипотезу $Н_{0} : D[Х] = D[Y]$ о равенстве генеральных дисперсий, при конкурирующей гипотезе$Н_{1} : D[X] > D[Y]$.

 По двум независимым выборкам, объем которых $n_{1} = 9$ и $n_{2} = 16$, извлеченным из нормальных генеральных совокупностей $Х$ и $Y$, найдены выборочные дисперсии $D_x^\ast = 20,2$ и $D_y^\ast = 14$. При уровне значимости $\alpha =0,05$ проверьте нулевую гипотезу $Н_{0} : D[Х] = D[Y]$ о равенстве генеральных дисперсий при конкурирующей гипотезе $Н_{1} : D[X] \ne D[Y]$.

 Проведено исследование розничного товарооборота продовольственных магазинов в двух районах Ярославской области (по 20 магазинов в каждом). Априори известны средние значения розничного товарооборота - 78,8 и 78,56 тыс. руб. Полученные в результате оценки средних квадратичных отклонений в первом и втором районах соответственно равны 7,2 и 7,8 тыс. руб. Можно ли считать, что разброс розничного товарооборота магазинов в районах неодинаков при уровне значимости $\alpha = 0,1$? Можно ли сделать вывод о разной покупательной способности населения районов?

 По выборке объема $n_{1} = 30$ найден средний вес $х^{\ast }=130$г. изделий, изготовленных на первом станке; по выборке объема $n_{2} = 40$ найден средний вес $y^{\ast }=125$г. изделий, изготовленных на втором станке. Генеральные дисперсии известны: $D[X] = 60 \mbox{г}^{2}, D[Y] = 80 \mbox{г}^{2}$. Проверьте нулевую гипотезу $Н_{0} : М[Х] = М[Y]$ при конкурирующей гипотезе $М[Х] \ne М[Y]$ и уровне значимости 0,05. Предполагаем, что случайные величины $Х$ и $Y$ распределены нормально и выборки независимы.

Исследование пропусков по болезни детей в двух группах детского сада в течение года (по 16 детей в каждой группе) дало следующие результаты: $x^{\ast}= 32$дня, $y^{\ast }= 41$день, $S_x^2 =\mbox{дней}^{2}$, $S_y^2 = 17\mbox{дней}^{2}$.

Можно ли считать, что среднее количество дней пропусков по болезни в обеих группах одинаково при уровне значимости $\alpha = 0,1$?

 Из нормальной генеральной совокупности с известным средним квадратическим отклонением $\sigma = 10$ известна выборка объема $n = 36$, и по ней найдена выборочная средняя$х^{\ast } = 107,5$. Проверьте нулевую гипотезу $Н_{0} : a = a_{0} = 110$ при конкурирующей гипотезе $Н_{1} : a \ne 110$ и уровне значимости 0,01.

Из двух партий изделий, изготовленных на двух одинаково настроенных станках, известны малые выборки, объемы которых $n_{1} = 12$ и $n_{2} = 15$. Получены следующие результаты:

Контролируемый размер

изделий первого станка

3,4

3,5

3,8

3,9

Число изделий

2

4

5

1

 

Контролируемый размер

изделий второго станка

3,2

3,4

3,7

 

Число изделий

4

3

8

 

Проверьте нулевую гипотезу о равенстве средних размеров изделий при уровне значимости 0,05.

По 100 независимым испытаниям найдена относительная частота $m/n = 0,15$. При уровне значимости 0,05 проверьте нулевую гипотезу $Н_{0} : р = р_{0} = 0,2$ при конкурирующей гипотезе а) $Н_{1}: р \ne 0,2$; б) $Н_{1} : р < р_{0}$ .

В банке в течение двух дней проводилось исследование времени обслуживания клиентов, данные которого представлены в таблице:

Номер

интервала

Время обслуживания (мин.)

Число клиентов в

1-й день

Число клиентов во 2-й день

1

2

3

4

5

6

7

6-8

8-10

10-12

12-14

14-16

16-18

18-20

2

3

8

12

15

10

3

3

4

9

13

17

8

3

Можно ли считать одинаковыми отклонения от среднего времени обслуживания клиентов банка в 1-й и 2-й дни при $\alpha =0,05$?

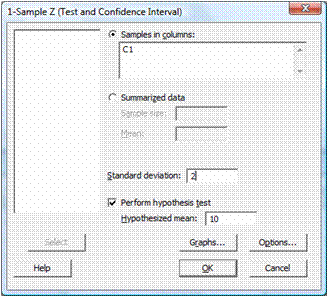
За смену отказали 20 элементов первого устройства, состоящего из 800 элементов, и 30 элементов второго, состоящего из 1000 элементов. При уровне значимости $\alpha = 0,01$ проверьте нулевую гипотезу $Н_{0} = р_{1} = р_{2} = р$ о равенстве вероятностей отказа элементов обоих устройств при конкурирующей гипотезе $Н_{1} : р_{1} \ne р_{2}$.

 

 

 

Любое недоказанное утверждение или догадку можно считать гипотезой. Статистическая гипотеза является предположением об одном или нескольких параметрах функции распределения случайной величины. К примеру, можно предположить, что генеральная совокупность данных распределена согласно нормальному закону или две выборки принадлежат двум разным популяциям, или различие между дисперсиями двух выборок статистически незначимо и т.д.

Статистические гипотезы проверяются на основании выборочных опытов/наблюдений. Поэтому вероятность той или иной гипотезы никогда не может быть принята однозначно равной 0 или 1. Вместо этого используются допустимые уровни вероятности: α и 1-α (или β). В практике статистического анализа чаще всего имеют дело с двумя конкурирующими гипотезами: нулевой гипотезой, обозначаемой H0, и альтернативной гипотезой, обозначаемой Hα или H1.

Нулевая гипотеза – это утверждение, подлежащее проверке. Альтернативная гипотеза – это противоположное утверждение, которое мы пытаемся опровергнуть в ходе анализа. В зависимости от величины вероятности альтернативная гипотеза может быть принята либо отвергнута. Нулевая гипотеза может быть отвергнута, но не принята! В случае высокого уровня вероятности правдивости нулевой гипотезы, говорят, что гипотеза не может быть отвергнута.

Принятие решений о генеральной совокупности на основе выборочных данных приводит к возможности постановки неправильного вывода. Различают два вида ошибок, связанных с постановкой вывода на основе выборочных данных:

·         Ошибка первого рода – возникает, когда отвергается нулевая гипотеза, при этом являясь правильной.

·         Ошибка второго рода – возникает, когда принимается нулевая гипотеза, при этом являясь ложной.

Чем ниже показатель α (вероятность ошибки первого рода), тем больше уверенность в правдивости нулевой гипотезы и наоборот.

В качестве примера наблюдений для проверки статистических гипотез используем набор из 100 значений со средним 10 и стандартным отклонением 2, сгенерированных программой Minitab 16. Рабочий файл, содержащий набор значений и результаты анализа, прикреплен к статье и доступен для всех зарегистрированных пользователей.

В меню Stat выберите Basic Statistics, а затем тест, необходимый для проверки статистической гипотезы. Используем 1-Sample Z… так как и закон распределения и стандартное отклонение нам известны (оба параметра заданы при генерации данных).

В появившемся окне внесем следующие настройки:

1. В поле Samples in columns: укажите диапазон анализируемых данных (C1 в данном случае)
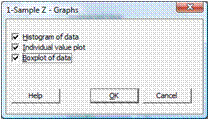
 2. В строке Standard deviation: введите значение стандартного отклонения – 2
 3. Поставьте флажок напротив Perform hypothesis test и укажите Hypothezed mean (величина, с которой будет сравнено среднее арифметическое значение наблюдений) – 10

 

 

4. Нажав на Graphs… можно выбрать три вида диаграмм, которые будут построены вместе с проверкой гипотезы – установите флажок напротив каждой их них:

 

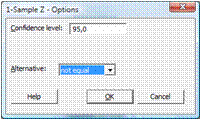
5. В меню Options… можно установить доверительный интервал (1 – α, по умолчанию установлено значение 95%) и альтернативную гипотезу – выберите "not equal” (не равно):

 

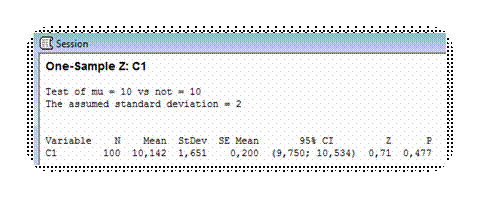
После внесения всех настроек, нажмите OK и перейдите в окно Session:

 

Интерпретация полученных результатов:

·         Variable – столбец переменных

·         N – число наблюдаемых значений

·         Mean – среднее арифметическое значение

·         StDev – стандартное отклонение.

·         SE Mean – средняя стандартизированная ошибка

·         95% CI – доверительный интервал

·         Z – Z-значение, используется для расчета Р

·         P – вероятность

Наибольший интерес, из полученных результатов, представляет величина Р – вероятность того, что нулевая гипотеза может быть принята. Для постановки вывода следует сравнить величину Р с α-уровнем:

·         Если Р ≤ α, то нулевая гипотеза отвергается и принимается альтернативная.

·         Если Р > α, то альтернативная гипотеза отвергается. В таком случае говорят, что нулевая гипотеза не может быть отвергнута – несмотря на то, что альтернативная отвергнута, нулевую гипотезу никогда не принимают.

α-уровень задается исследователем при настройке доверительного интервала: доверительный интервал равен 1 – α. Следовательно, при значении доверительного интервала 95%, α-уровень равен 5%. Для проверки статистической гипотезы можно задать любое значение α-уровня от 0 до 1, на чаще всего используют величину 0,05 или 5%.

В рассмотренном случае значение Р составляет 0,477, при этом α-уровень – 0,05, соответственно с большой долей вероятности можно утверждать, что нулевая гипотеза не может быть отвергнута: среднее арифметическое значение наблюдаемых результатов равно 10.

Ниже представлены, полученные в ходе проверки гипотез, диаграммы:

 

Фактически показания диаграмм идентичны: расчетное значение попадает в пределы доверительного интервала и близко к 10. Разница между диаграммами состоит лишь в способе отображения распределения наблюдаемых значений: гистограмма, точечная или ящичная диаграммы.

 

Статистическая мощность (реже "чувствительность") (англ. statistical power) - это вероятность того, что тот или иной статистический критерий правильно отклонит неверную нулевую гипотезу. Иными словами - это способность критерия обнаружить различия там, где они действительно существуют. Обычно процесс проверки статистической гипотезы включает следующие шаги:

·                     Формулировка собственно проверяемой нулевой гипотезы. Например, в случае двухвыборочного критерия Стьюдента она состоит в том, что обе выборки происходят из нормально распределенных генеральных совокупностей с одинаковыми средними значениями (подробнее см. здесь).

·                     Выбор подходящего статистического критерия для проверки нулевой гипотезы. Вычисление значения этого критерия по имеющимся выборочным данным.

·                     Определение критического значения критерия, исходя из желаемого уровня статистической значимости αи свойств теоретического распределения этого критерия.

·                     Проверка того, превышает ли рассчитанный по выборочным данным критерий критическое значение. Если такое превышение не наблюдается, делают вывод о том, что нулевая гипотеза верна.


Не обнаружив различий, исследователь, к сожалению, часто делает вывод об их действительном отсутствии. Однако проблема заключается в том, что такой вывод не всегда будет верным, т.к. сравнивая случайные выборки исследователь, как известно, неизбежно рискует совершить одну из двух типов ошибок:

·                     Ошибка первого типа (= "первого рода"): отклонение верной нулевой гипотезы. Риск совершить такую ошибку равен выбранному уровню значимости (например,  α=0.05).

·                      Ошибка второго типа (= "второго рода"): сохранение неверной нулевой гипотезы. Вероятность ошибочно сохранить неверную нулевую гипотезу обозначают буквой β.

Таким образом, прежде чем сделать вывод об остутствии различий, исследователь должен выяснить, была ли мощность использованного статистического критерия достаточной для их обнаружения. Уровень β-риска тесно связан с 1) величиной различий между выборками (т.н. "величиной эффекта"), 2) числом наблюдений и 3) разбросом данных. Наиболее важным является число наблюдений: чем больше размер выборок, тем выше мощность теста. При "достаточно" больших выборках даже небольшие различия окажутся статистически значимыми. И наоборот - при малых выборках даже большие различия выявить будет трудно. Зная эти закономерности, мы можем заранее (т.е. до проведения исследования) определить минимальный размер выборок, необходимый для выявления эффекта.

На практике обычно (но не всегда) приемлемой считается мощность теста, равная или превышающая 80% (что соответствует β-риску в 20%). Этот уровень является следствием т.н. "соотношения 1 к 4" (англ. "one-to-four trade-off") между уровнями α-риска и β-риска: если принять уровень значимости α=0.05, тогда β=0.05×4=0.20и мощность критерия составит Π=1−0.20=0.80.

При проведении вычислений, связанных с мощностью критерия Стьюдента, нам придестя оперировать следующими параметрами:

·                     Величина эффекта, которую мы хотим выявить в ходе исследования ("дельта", т.е. разница между средними значениями сравниваемых выборок).

·                     Стандартное отклонение (предполагается, что оно статистически не различается в сравниваемых выборках).

·                     Уровень значимости, α.

·                     Мощность критерия (обычно выражается в %).

·                     Объем выборки

 

Источник: lifecity.com.ua

В качестве примера предположим, что мы планируем проведение эксперимента для установления эффекта температуры на индивидуальный вес водного жука. В эксперименте будут задействованы два температурных режима и, соответственно, установление эффекта температуры мы будем проверять, сравнивая средние значения веса жуков из двух экспериментальных групп при помощи двустороннего критерия Стьюдента (двусторонний вариант выбран потому, что до проведения эксперимента мы не знаем, каков именно эффект окажет повышение температуры - повышение или понижение веса жуков). Проверяемая в данном случае нулевая гипотеза состоит в том, что температура не оказывает никакого влияния на вес жуков.

 

Допустим, что минимальная разница в среднем весе жуков, которую мы хотим выявить в ходе эксперимента, составляет 3 мг. При уровне значимости α=0.05 желаемая мощность теста должна составить 80%. Вопрос заключается в том, сколько животных мы должны задействовать в эксперименте для того, чтобы перечисленные условия были выполнены. Как следует из приведенного выше списка, для определения оптимального размера выборки нам необходимо знать стандартное отклонение веса изучаемого вида жуков. К сожалению, до проведения эксперимента мы не можем точно оценить этот параметр. Вариантов решения этой проблемы два: 1) основываясь на своем экспертном мнении, исследователь может дать примерную оценку стандартного отклонения; 2) можно попытаться найти соответствующие литературные данные. Предположим, что мы воспользовались вторым вариантом и выяснили, что стандартное отклонение веса для изучаемого вида жуков составляет 1.8 мг.

Теперь у нас есть вся необходимая информация для расчета минимального объема выборки. В R соответствующие вычисления можно выполнить при помощи базовой функции power.t.test():

 

power.t.test(delta = 3.0,
              sd = 1.8,
              sig.level = 0.05,
              power = 0.8)
 
     Two-sample t test power calculation 
 
              n = 6.76095
          delta = 3
             sd = 1.8
      sig.level = 0.05
          power = 0.8
    alternative = two.sided
 
 NOTE: n is number in *each* group

 

В приведенной выше команде delta - минимальная величина эффекта, которую мы хотим обнаружить в ходе эксперимента, sd - стандартное отклонение веса жуков (по литературным данным), sig.level - уровень значимости, а power - мощность t-критерия. В результатах вычислений программа еще раз перечисляет имеющиеся исходные параметры, а также сообщает n - рассчитанный минимальный размер каждой выборки для обнаружения желаемого эффекта при этих параметрах (округлив, получаем 7 жуков в каждой экспериментальной группе). Кроме того, программа напоминает нам, что вычисления были выполнены для двустроннего критерия Стьюдента (alternative = two.sided) и что параметр n соответствует числу наблюдений в каждой группе (n is number in *each* group).


Зная число наблюдений, величину эффекта, стандартное отклонение и уровень значимости мы можем рассчитать мощность теста. Например:

power.t.test(n = 15,
              delta = 3.0,
              sd = 1.8,
              sig.level = 0.05)
 
     Two-sample t test power calculation 
 
              n = 15
          delta = 3
             sd = 1.8
      sig.level = 0.05
          power = 0.9927162
    alternative = two.sided
 
 NOTE: n is number in *each* group



Как видим, при n = 15, delta = 3, sd = 1.8 и sig.level = 0.05 мощность критерия составит 99%.

При необходимости выполнить вычисления для парного критерия Стьюдента, в вызов функции power.t.test()достаточно добавить аргумент type = "paired":

power.t.test(delta = 3.0,
               sd = 1.8,
               sig.level = 0.05,
               power = 0.8,
               type  = "paired")
 
     Paired t test power calculation 
 
              n = 5.04919
          delta = 3
             sd = 1.8
      sig.level = 0.05
          power = 0.8
    alternative = two.sided
 
 NOTE: n is number of *pairs*, sd is std.dev. of *differences* within pairs


 Как видим, в случае с зависимыми выборками минимальный размер выборок, необходимый для выявления заданной величины эффекта, несколько меньше, чем в случае с независимыми выборками (в рассматриваемом примере - 5 против 7 жуков в каждой группе).

Наконец, при необходимости выполнить одновыборочный t-тест аргументу type следует присвоить значение"one.sample":

power.t.test(delta = 3.0,
               sd = 1.8,
               sig.level = 0.05,
               power = 0.8,
               type  = "one.sample")
 
     One-sample t test power calculation 
 
              n = 5.04919
          delta = 3
             sd = 1.8
      sig.level = 0.05
          power = 0.8
    alternative = two.sided


В заключение следует еще раз подчеркнуть, что если в ходе выполнения t-теста проверяемая нулевая гипотеза не отклонена, это не значит, что эффект в действительности остутствует. Возможно, объемы выборок были просто недостаточно велики для этого. Поэтому рекомендуется приводить в отчетах (статьях, презентациях, и т.п.) не только результаты статистического теста как такового, но еще и информацию о его мощности. Это позволит читателям отчета сформировать четкое представление о том, носколько полученные данные поддерживают сделанные по результатам анализа выводы.