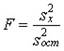|
Раздел 9. Дисперсионный анализ
Может быть поставлена задача сравнения двух выборочных дисперсий. Для ее решения применяется критерий, названный в честь английского статистика Рональда Фишера (1890 - 1968) F критерием. Этот критерий представляет собой отношение выборочных дисперсий s21 иs22, которые рассматриваются как оценки одной и той же генеральной дисперсии σ2:
Испытуемая гипотеза является нулевой гипотезой Н0 : σ21 = σ22 = σ2, альтернативная гипотеза Н1 : σ21 ? σ22 ? σ2 . F - критерий строится так, что в числителе стоит большая дисперсия. Fmin = 1, Fmax → ∞ .Критические значения критерия F берутся из таблиц F-распределения. F-распределение зависит от уровня значимости и от числа степеней свободы сравниваемых дисперсий d.f.1 и d.f.2 (cм. приложение, табл. 3). В дисперсионном анализе общая вариация подразделяется на составляющие и производится сравнение этих составляющих. Испытуемая гипотеза состоит в том, что если данные каждой группы представляют случайную выборку из нормально распределенной генеральной совокупности, то величины всех частных дисперсий должны быть пропорциональны своим степеням свободы и каждую из них можно рассматривать как оценку генеральной дисперсии. Дисперсионный анализ часто применяется совместно с аналитической группировкой (см. гл. 6). Вэтом случае данные подразделяются на группы по значениям признака-фактора, вычисляются значения средних величин результативного признака в группах, считается, что различия в их значениях определяются различиями в значениях фактора. Задача состоит в оценке существенности различий между средними значениями результативного признака в группах.Итак, испытуемая гипотеза может быть записана как гипотеза о средних величинах Н0 : μ1 = μ2=μ3 =… Как было показано в предыдущем параграфе, когда выделяются две группы, этазадача решается с помощью t-критерия. Если же число сравниваемых групп больше двух, тосущественность различий между группами доказывается с помощью дисперсионного анализа,на основе F-критерия. Заметим, что результаты дисперсионного анализа, так же как и выводыо характере связи, значения показателей ее силы и тесноты, зависят от числа групп,выделенных по признаку-фактору. В случае выделения групп по одному фактору мы имеем так называемый однофакторный дисперсионный комплекс. Разложение дисперсии при этом производится в соответствии справилом сложения дисперсий (см. гл. б):
где уij - значение результативного признака у i-й единицы в j-й группе; i - номер единицы, i = 1, .... п.; j - номер группы; пj- численность у-й группы; yj - средняя величина результативного признака в у-й группе; у? — общая средняя результативного признака.
Если обозначить суммы квадратов отклонений буквой D, получим равенство: Dобщ = Dфакт +Dост (7.41) На основе разложения дисперсии (7.41) в соответствии с гипотезой отсутствия различий междугруппами могут быть получены три оценки генеральной дисперсии, пропорциональные степенисвободы: на основе общей вариации, межгрупповой (факторной) и внутригрупповой(остаточной). Число степеней'свободы равно:
для общей вариации
для межгрупповой вариации
для внутригрупповой вариации Как и суммы квадратов отклонений, числа степеней свободы связаны между собой равенством:
или п - 1 = (m - 1) + (п - т). (7.42)
Деление сумм квадратов отклонений на соответствующее число степеней свободы дает триоценки генеральной дисперсии σ2 .
Поскольку Dфакт измеряет вариацию результативного признака, связанную с изменениемфактора, по которому произведена группировка, a Dост - вариацию, связанную с изменениемвсех прочих факторов, сравнение этих величин, рассчитанных на одну степень свободы, даетвозможность оценить существенность влияния признака-фактора на результативный признак спомощью F-критерия:
Эта запись предполагает, что s2факт > s2ост. Как правило, мы получаем именно такоесоотношение. Если F факт > Fтабл (α., d.f.1, d.f.2), можно утверждать, что нуль-гипотеза несоответствует фактическим данным, влияние признака-фактора является существенным или,иначе говоря, статистически значимым. Рассмотренные этапы однофакторного дисперсионного анализа представлены в табл. 7.9. Таблица 7.9 Схема однофакторного дисперсионного анализа
По данным табл. 6.6 проверим гипотезу Н0 : μ 1= μ2 ..., т. е. предположим, что оборачиваемость средств никак не влияет на прибыль. Dфакт = 172,76, d.f.факт =3-1=2, σ21 = 86,38; Dост – Dобщ - Dфакт = 224,4 - 172.76 = 51,64; d.f.ост = 20 - 3=17; s22 = 3,03. Тогда F = 28,5. Критическое значение F-критерия из табл. 3 приложения F(α=0,05, d.f.1=2,d.f.2=17) = 3,59. Таким образом Fфакт > Fкрит следовательно, Н0 отклоняется.Действительно, скорость оборота средств является очень важным фактором формированияприбыли, на это указывало и значение эмпирического корреляционного отношения η = 0,881. Рассмотрим двухфакторный дисперсионный анализ, основой проведения которого служиткомбинационная группировка по двум факторам х и z, с последующим разложением дисперсиирезультативного признака у:
где i - номер единицы в j-й группе по признаку х и k-й по признаку z; j = 1?,т?, k =I?р?, у?jk - среднее значение признака у? в группе, образованной комбинацией j-го значенияпризнака х и k-го значения признака z; у?j - среднее значение признака у в j-й группе по признаку х; y?k - среднее значение признака у в k-й группе по признаку z; у? - общая средняя признака y в целом по выборке; пjk - число единиц в группе, образованной комбинацией j-го значения признака х и k-го значенияпризнака z; пj - число единиц в j-й группе по признаку х, пk - число единиц в k-й группе по признаку z; т Р т р
п-
общее число единиц,
Равенство (7.44) можно записать так: Dобщ = Dx + Dz + Dxz + Dост (7.45) где Dч - вариация у под влиянием фактора x; Dz - вариация у под влиянием фактора z; Dxz - вариация у, обусловленная взаимодействием факторов х и z; Dост - вариация у под влиянием прочих факторов.
Первые три слагаемые составляют вариацию признака у, вызванную изучаемыми факторами,поэтому равенство (7.45) можно записать в виде: Dобщ = Dфакт +Dост (7.46) где Dфакт = Dх + Dz + Dxz. (7.47)
Величина Dфакт может быть рассчитана не через составляющие, а непосредственно как
Однако при неравенстве численностей подгрупп пjk и групп пj и пk равенство нарушается (засчет взвешивания при неравных весах). Поэтому рассчитываются невзвешенные величины:
Затем на основе сравнения взвешенной (7.48) и невзвешенной величин факторной дисперсиинаходят поправочный коэффициент:
Этот коэффициент используется для корректировки невзвешенных сумм
квадратов отклонений
Число степеней свободы для каждой суммы квадратов отклонений составляет: d.f.x=m- 1; d.f.z = p - 1; d.f.xz = (m-1)(p -1) = mp - т - р + 1, в целом d.f.факт = d.f.x + d.f.z + d.f.xz = mp-1;
В двухфакторном дисперсионном анализе испытуемые гипотезы формулируются следующимобразом: 1. Н0 : μ1• = μ2. =…μm 2. Н0 : μ1• = μ2. =…μp 3. Н0 : μ1• = μ2. =…μmp Вся процедура двухфакторного дисперсионного анализа обобщается в табл. 7.10. Таблица 7.10 Схема двухфакторного дисперсионного анализа
Решение о первой гипотезе принимается на основе сравнения
Если Fфакт > Fкрит, то Н0 отклоняется. Вторая гипотеза испытывается на основе сравнения
Третья - на основе сравнения
Во всех случаях, если Fфакт > Fкрит, Н0 отклоняется. На основе F-критерия принимаютсярешения о форме уравнения регрессии, о статистической з начимости той или иной объясняющейпеременной при построении многофакторного уравнения регрессии (см. гл. 8) и др. Рассмотренные направления проверки статистических гипотез охватывают лишь важнейшие изних. Процедура испытания статистических гипотез применяется для определения того,случайно или нет полученное значение коэффициента корреляции, коэффициента вариации и т.д., случайны или нет различия в значениях показателей (медиан, коэффициентов корреляции,регрессии и т.д.) в разных совокупностях. Во всех случаях результатом являетсявероятностное суждение, которое составляет сущность анализа данных в разнообразныхсферах: в медицине, биологии, технике, политике, спорте, экономике, психологии и социологии. |
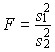 .
.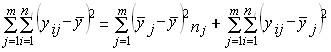 ,
,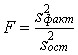 .
.
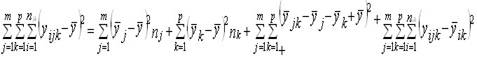 (7.44)
(7.44)