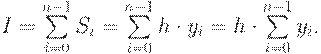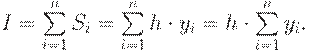Метод прямоугольников

Словесный алгоритм метода прямоугольников:

Весь участок [a,b] делим на n равных частей с шагом h=(b-a)/n.
Определяем значение yi подынтегральной функции f(x) в каждой части деления, т.е.

$Описание: y_i=f(x_i), i=\overline{0,n}.$

В каждой части деления подынтегральную функцию f(x) аппроксимируем интерполяционным многочленом степени n = 0, т.е. прямой, параллельной оси OX. В результате вся подынтегральная функция на участке [a,b] аппроксимируется ломаной линией.
Для каждой части деления определяем площадь Si частичного прямоугольника.
Суммируем эти площади. Приближенное значение интеграла I равно сумме площадей частичных прямоугольников.

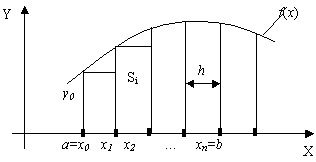
Если высота каждого частичного прямоугольника равна значению подынтегральной функции в левых концах каждого шага, то метод называется методом левых прямоугольников (рис.12.3). Тогда квадратурная формула имеет вид

$Описание: I=\sum \limits_{i=0}^{n-1}S_i = \sum \limits_{i=0}^{n-1}h \cdot y_i = h \cdot \sum \limits_{i=0}^{n-1}y_i.$

Описание: Метод левых прямоугольников

Рис. 12.3. Метод левых прямоугольников

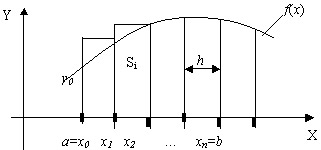
Если высота каждого частичного прямоугольника равна значению подынтегральной функции в правых концах каждого шага, то метод называется методом правых прямоугольников (рис.12.4). Тогда квадратурная формула имеет вид

$Описание: I=\sum \limits_{i=1}^{n}S_i = \sum \limits_{i=1}^{n}h \cdot y_i = h \cdot \sum \limits_{i=1}^{n}y_i.$

Описание: Метод правых прямоугольников

Рис. 12.4. Метод правых прямоугольников

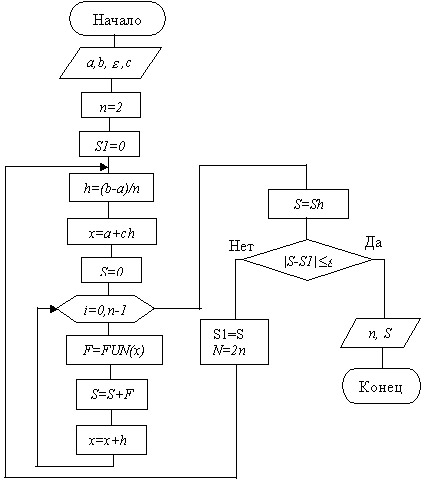
Точность каждого метода прямоугольников имеет порядок h.

Алгоритм вычисления интеграла построим в виде итерационного процесса поиска с автоматическим выбором шага. На каждом шаге будем уменьшать шаг в два раза, то есть увеличивать число шагов n в два раза. Выход из процесса поиска организуем по точности вычисления интеграла. Начальное число шагов n=2.Схема алгоритма методов прямоугольников представлена на рис.12.5.

Описание: Схема алгоритма метода прямоугольников (с автоматическим выбором шага)

Рис. 12.5. Схема алгоритма метода прямоугольников (с автоматическим выбором шага)

Условные обозначения:

a,b - концы интервала,

$Описание: \varepsilon$ - заданная точность,

с=0 - метод левых прямоугольников,

с=1 - метод правых прямоугольников,

S1 - значение интеграла на предыдущем шаге,

S - значение интеграла на текущем шаге.