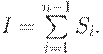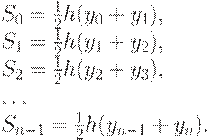Метод трапеций

Словесный алгоритм метода трапеций:

Интервал [a,b] делим на n равных частей с шагом h=(b-a)/n.

Вычисляем значение подынтегральной функции в каждой узловой точке

$Описание: y_i=f(x), i=\overline{0,n}.$

На каждом шаге подынтегральную функцию f(x) аппроксимируем прямой, соединяющей две соседние узловые точки. В результате вся подынтегральная функция на участке [a,b] заменяется ломаной линией проходящей через все узловые точки.

Вычисляем площадь каждой частичной трапеции.

Приближенное значение интеграла равно сумме площадей частичных трапеций, т.е.

$Описание: I=\sum \limits_{i=1}^{n-1}S_i.$

Найдем площади Si частичных трапеций:

$Описание: S_0=\frac{1}{2}h(y_0+y_1),\\ S_1=\frac{1}{2}h(y_1+y_2),\\ S_2=\frac{1}{2}h(y_2+y_3),\\ \ldots\\ S_{n-1}=\frac{1}{2}h(y_{n-1}+y_n).$

Приближенное значение интеграла равно

$Описание: I=\sum \limits_{i=1}^{n-1}S_i = \frac{h}{2} \sum \limits_{i=1}^{n}(y_i + y_{i+1}) = \frac{h}{2}(y_0 + y_n + 2\sum \limits_{i=1}^{n-1}y_i).$

Точность метода трапеций имеет порядок h2.

Схема алгоритма метода трапеций представлена на рис.12.6.

Описание: Схема алгоритма метода трапеций (с автоматическим выбором шага)

Рис. 12.6. Схема алгоритма метода трапеций (с автоматическим выбором шага)