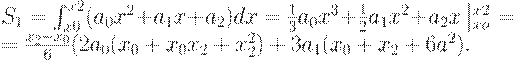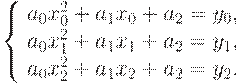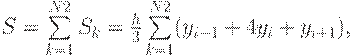Метод Симпсона

В методе Симпсона в каждой части деления подынтегральная функция аппроксимируется квадратичной параболой a0x2+a1x+a2. В результате вся кривая подынтегральной функции на участке [a,b] заменяется кусочно-непрерывной линией, состоящей из отрезков квадратичных парабол. Приближенное значение интеграла I равно сумме площадей под квадратичными параболами.

Т.к. для построения квадратичной параболы необходимо иметь три точки, то каждая часть деления в методе Симпсона включает два шага, т.е.

Lk=2h.

В результате количество частей деления N2=n/2. Тогда n в методе Симпсона всегда четное число.

Определим площадь S1 на участке [x0, x2] (рис.12.2).

Исходя из геометрического смысла определенного интеграла, площадь S1 равна определенному интегралу от квадратичной параболы на участке [x0, x2]:

$Описание: S_1=\int_{x0}^{x2}(a_0x^2 + a_1x + a_2)dx = \frac{1}{3}a_0x^3 + \frac{1}{2}a_1x^2 + a_2x\left|_{xo}^{x2} \right. =\\ = \frac{x_2-x_0}{6}(2a_0(x_0 + x_0x_2 +x_2^2) + 3a_1(x_0 + x_2 + 6a^2).$

Неизвестные коэффициенты квадратичной параболы а0 , а1, а2 определяем из условия прохождения параболой через три узловых точки с координатами (x0y0), (x1y1), (x2y2).

На основании этого условия строим систему линейных уравнений:

$Описание: \left\{ \begin{array}{l} a_0x_0^2 + a_1x_0 + a_2 = y_0,\\ a_0x_1^2 + a_1x_1 + a_2 = y_1,\\ a_0x_2^2 + a_1x_2 + a_2 = y_2. \end{array} \right.$