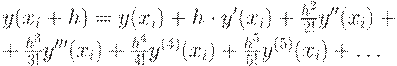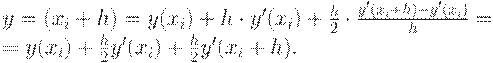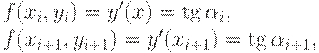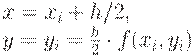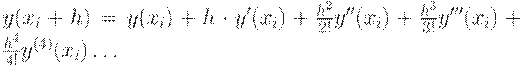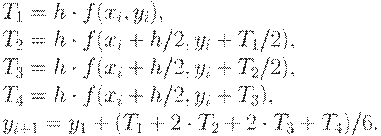Методы Рунге - Кутта

Наиболее эффективными и часто встречаемыми методами решениями задачи Коши являются методы Рунге - Кутта. Они основаны на аппроксимации искомой функции у(х) в пределах каждого шага многочленом, который получен при помощи разложения функции у(х) в окрестности шага h каждой i-ой точки в ряд Тейлора:

$Описание: y(x_i+h) = y(x_i) + h \cdot y'(x_i) + \frac{h^2}{2!}y''(x_i) + \\ + \frac{h^3}{3!}y'''(x_i) + \frac{h^4}{4!}y^{(4)}(x_i) + \frac{h^5}{5!}y^{(5)}(x_i) + \ldots$

( 12.4)

Усекая ряд Тейлора в различных точках и отбрасывая правые члены ряда, Рунге и Кутта получали различные методы для определения значений функции у(х) в каждой узловой точке. Точность каждого метода определяется отброшенными членами ряда.

Метод Рунге - Кутта 1-го порядка (метод Эйлера)

Отбросим в (12.4) члены ряда, содержащие h2, h3, h4:.

Тогда $Описание: y(x_i+h)=y(x_i)+h \cdot y'(x_i)$ .

Так как

Получим формулу Эйлера:

$Описание: y_{i+1}=y_i + h \cdot f(x_i,y_i)$

( 12.5)

Так как точность методов Рунге-Кутта определяется отброшенными членами ряда (12.4), то точность метода Эйлера на каждом шаге составляет $Описание: \approx h^2$ .

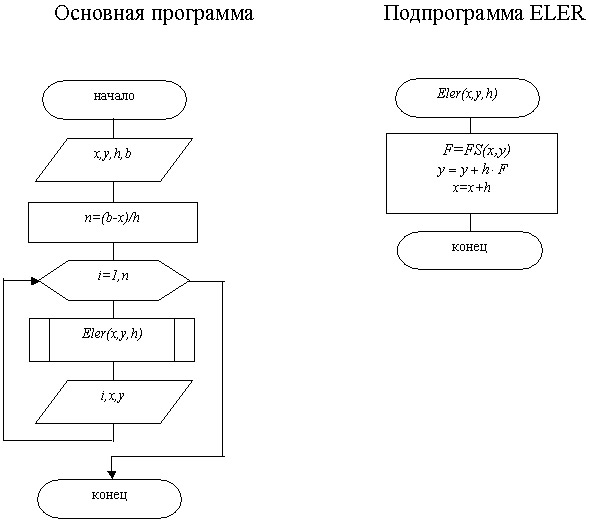
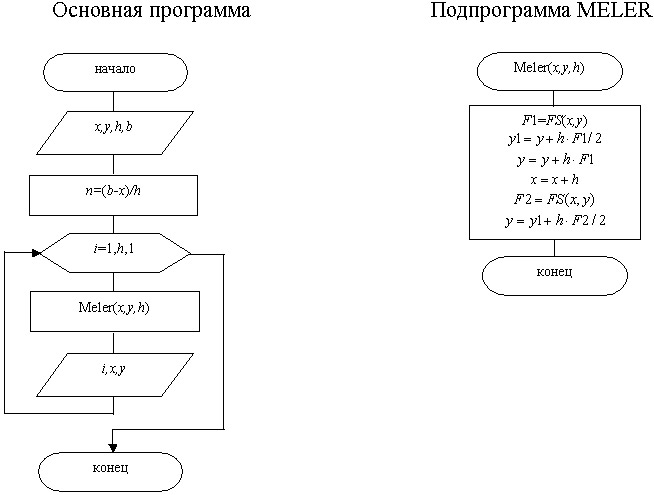
Алгоритм метода Эйлера можно построить в виде двух программных модулей: основной программы и подпрограммы ELER, реализующей метод.

Описание: Схема алгоритма метода Эйлера

Рис. 12.10. Схема алгоритма метода Эйлера

Здесь

(x,y) -при вводе начальная точка, далее текущие значения табличной функции,

h -шаг интегрирования дифференциального уравнения,

b -конец интервала интегрирования.

Рассмотрим геометрический смысл метода Эйлера.

Формула Эйлера имеет вид:

$Описание: y_{i+1}=y_i + h \cdot f(x_i,y_i),$

где $Описание: f(x_i,y_i) = y'(x_i) = \tg\alpha_i$ .

Тогда формула Эйлера принимает вид:

$Описание: y_{i+1}=y_i + h \cdot \tg\alpha_i,$

где

$Описание: \tg\alpha_i$ - тангенс угла наклона касательной к искомой функции у(x) в начальной точке каждого шага.

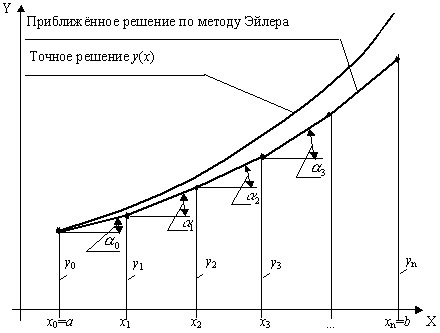
Описание: Геометрический смысл метода Эйлера

Рис. 12.11. Геометрический смысл метода Эйлера

В результате в методе Эйлера на графике (рис 12.10) вся искомая функция y(x) на участке [a,b] аппроксимируется ломаной линией, каждый отрезок которой на шаге h линейно аппроксимирует искомую функцию. Поэтому метод Эйлера получил еще название метода ломаных.

В методе Эйлера наклон касательной в пределах каждого шага считается постоянным и равным значению производной в начальной точке шага xi. В действительности производная, а, значит, и тангенс угла наклона касательной к кривой y(x) в пределах каждого шага меняется. Поэтому в точке xi+h наклон касательной не должен быть равен наклону в точке xi. Следовательно, на каждом шаге вносится погрешность.

Первый отрезок ломаной действительно касается искомой интегральной кривой y(x) в точке (x0,y0). На последовательных же шагах касательные проводятся из точек (xi,yi), подсчитанных с погрешностью. В результате с каждым шагом ошибки накапливаются.

Основной недостаток метода Эйлера - систематическое накопление ошибок. Поэтому метод Эйлера рекомендуется применять для решения дифференциальных уравнений при малых значениях шага интегрирования h.

Метод Рунге - Кутта 2-го порядка (модифицированный метод Эйлера)

Отбросим в (12.4) члены ряда, содержащие h3, h4, h5:.

Тогда

$Описание: y(x_i+h)=y(x_i)+h\cdot y'(x_i)+\frac{h^2}{2!} \cdot y"(x_i).$

( 12.6)

Чтобы сохранить член ряда, содержащий h2, надо определить вторую производную y"(xi).Ее можно аппроксимировать разделенной разностью 2-го порядка

$Описание: y"=(x_i)=\frac{\Delta y'}{\Delta x}= \frac{y'(x_i+h)-y'(x_i)}{h}$

Подставляя это выражение в (12.6), получим

$Описание: y=(x_i+h) =y(x_i) + h\cdot y'(x_i) + \frac{h}{2} \cdot \frac{y'(x_i+h)-y'(x_i)}{h}=\\ =y(x_i) + \frac{h}{2}y'(x_i) + \frac{h}{2}y'(x_i+h).$

Окончательно, модифицированная или уточненная формула Эйлера имеет вид:

$Описание: y_{i+1}=y_i + \frac{h}{2}f(x_i,y_i) + \frac{h}{2}f(x_{i+1},y_{i+1}).$

( 12.7)

Как видно, для определения функции y(x) в точке i+1 необходимо знать значение правой части дифференциального уравнения f(xi+1, yi+1) в этой точке, для определения которой необходимо знать предварительное значение yi+1.

Для определения предварительного значения yi+1 воспользуемся формулой Эйлера. Тогда все вычисления на каждом шаге по модифицированной или уточненной формуле Эйлера будем выполнять в два этапа:

На первом этапе вычисляем предварительное значение $Описание: y_{i+1}^Э$ по формуле Эйлера

$Описание: y_{i+1}^Э = y_i + hf(x_i,y_i).$

На втором этапе уточняем значение y=i+1 по модифицированной или уточненной формуле Эйлера

$Описание: y_{i+1} = y_i + \frac{h}{2}f(x_i,y_i) + \frac{h}{2}f(x_{i+1},y_{i+1}^Э).$

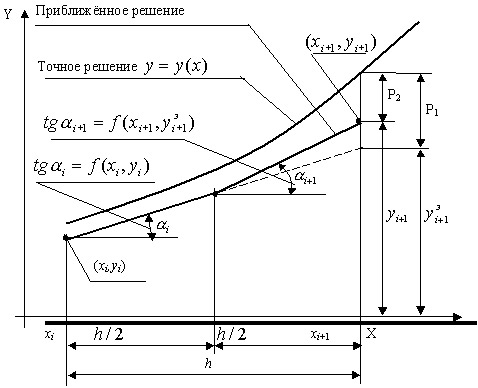
Точность метода определяется отброшенными членами ряда Тейлора (12.4), т.е. точность уточненного или модифицированного метода Эйлера на каждом шаге $Описание: \approx h^3$ .

Рассмотрим геометрический смысл модифицированного метода Эйлера.

Так как

$Описание: f(x_i,y_i) = y'(x) = \tg\alpha_i,\\ f(x_{i+1},y_{i+1}) = y'(x_{i+1}) = \tg\alpha_{i+1},$

то модифицированную формулу Эйлера можно представить в виде:

$Описание: y_{i+1} = y_I + \frac{h}{2}\tg\alpha_i + \frac{h}{2}\tg\alpha_{i+1},$

где

$Описание: \tg \alpha_i$ - тангенс угла наклона касательной к искомой функции у(х) в начальной точке каждого шага,

$Описание: \tg \alpha_{i+1}$ - тангенс угла наклона касательной к искомой функции у(х) в конечной точке каждого шага.

Описание: Геометрический смысл модифицированного метода Эйлера

Рис. 12.12. Геометрический смысл модифицированного метода Эйлера

Здесь

P1 - накопленная ошибка в (i+1)й точке по методу Эйлера,

P2 - накопленная ошибка в (i+1)й точке по модифицированному методу Эйлера.

Как видно из рис.12.11, в первой половине каждого шага, то есть на участке [xi, xi+h/2], искомая функция y(x) аппроксимируется прямой, которая выходит из точки (xi, yi) под углом, тангенс которого $Описание: \tg \alpha_i = f(x_i,y_i)$ .

Во второй половине этого же шага, т.е. на участке [xi + h/2,xi + h], искомая функция y(x) аппроксимируется прямой, которая выходит из точки с координатами

$Описание: x=x_i + h/2,\\ y=y_i = \frac{h}{2} \cdot f(x_i,y_i)$

под углом, тангенс которого

$Описание: \tg \alpha_{i+1} = f(x_{i+1},y_{i+1}^Э).$

В результате в модифицированном методе Эйлера функция у(х) на каждом шаге аппроксимируется не одной прямой, а двумя.

Алгоритм модифицированного метода Эйлера можно построить в виде двух программных модулей: основной программы и подпрограммы МELER, реализующей метод (рис. 12.13).

Описание: Схема алгоритма модифицированного метода Эйлера

Рис. 12.13. Схема алгоритма модифицированного метода Эйлера

Здесь

(x,y) -при вводе начальная точка, далее текущие значения табличной функции,

h -шаг интегрирования дифференциального уравнения,

b -конец интервала интегрирования.

Метод Рунге - Кутта 4-го порядка

Самое большое распространение из всех численных методов решения дифференциальных уравнений с помощью ЭВМ получил метод Рунге-Кутта 4-го порядка. В литературе он известен как метод Рунге-Кутта.

В этом методе на каждом шаге интегрирования дифференциальных уравнений искомая функция y(x) аппроксимируется рядом Тейлора (12.4), содержащим члены ряда с h4:

$Описание: y(x_i+h) = y(x_i) + h \cdot y'(x_i) + \frac{h^2}{2!}y''(x_i) + \frac{h^3}{3!}y'''(x_i) + \frac{h^4}{4!}y^{(4)}(x_i)\ldots$

В результате ошибка на каждом шаге имеет порядок h5.

Для сохранения членов ряда, содержащих h2,h3,h4 необходимо определить вторую y", третью y"' и четвертую y(4) производные функции y(x). Эти производные аппроксимируем разделенными разностями второго, третьего и четвертого порядков соответственно.

В результате для получения значения функции yi+1 по методу Рунге-Кутта выполняется следующая последовательность вычислительных операций:

$Описание: T_1=h \cdot f(x_i,y_i),\\ T_2=h \cdot f(x_i+h/2,y_i+T_1/2),\\ T_3=h \cdot f(x_i+h/2,y_i+T_2/2),\\ T_4=h \cdot f(x_i+h/2,y_i+T_3),\\ y_{i+1}=y_1+(T_1+2 \cdot T_2+2 \cdot T_3+T_4)/6.$

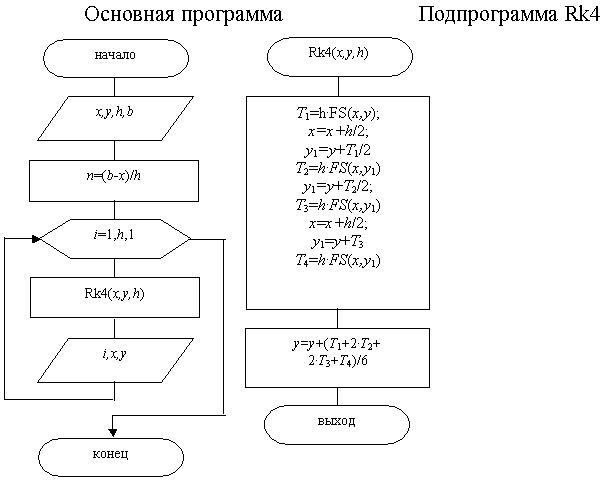
Вывод формулы не приведен. Предоставляется возможность вывод формул выполнить самостоятельно.

Алгоритм метода Рунге-Кутта (4-го порядка) можно построить в виде двух программных модулей: основной программы и подпрограммы Rk4, реализующей метод (рис 12.14).

Описание: Схема алгоритма метода Рунге-Кутта 4-го порядка.

Рис. 12.14. Схема алгоритма метода Рунге-Кутта 4-го порядка.

Здесь

(x,y) -при вводе начальная точка, далее текущие значения табличной функции,

h -шаг интегрирования дифференциального уравнения,

b -конец интервала интегрирования.