НЕПРЕРЫВНО-ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ (D-схемы)

Особенностью непрерывно-детерминированного подхода является применение в качестве математических моделей дифференциальные уравнений. Дифференциальными уравнениями называются такие уравнения, в которых неизвестными являются функции одной или нескольких переменных, причем в уравнение входят не только функции, но и их производные различных порядков. Если неизвестные — функции многих переменных, то уравнения называются уравнениями в частных производных, в противном случае при рассмотрении функции только одной независимой переменной уравнения называются обыкновенными дифференциальными уравнениями. Обычно в таких математических моделях в качестве независимой переменной, от которой зависят неизвестные искомые функции, служит время t. Тогда математическое соотношение для детерминированных систем в общем виде будет (5.1) где и — n-мерные векторы; —вектор-функция, которая определена на некотором (n + 1)-мерном множестве и является непрерывной. Так как математические схемы такого вида отражают динамику изучаемой системы, т. е. ее поведение во времени, то они называются D-схемами (англ. dynamic). В простейшем случае обыкновенное дифференциальное уравнение имеет вид (5.2) Наиболее важно для системотехники приложение D-схем в качестве математического аппарата в теории автоматического управления. 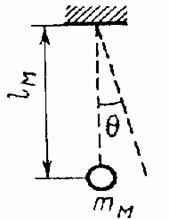Для иллюстрации особенностей построения и применения D-схем рассмотрим простейший пример формализации процесса функционирования двух элементарных систем различной физической природы: механической SM (колебания маятника, рис. 1); Рис 1. 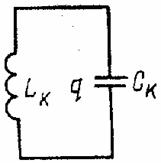электрической SX (колебательный контур, рис. 2). Рис 2. Процесс малых колебаний маятника описывается обыкновенным дифференциальным уравнением , где — масса и длина подвеса маятника; g — ускорение свободного падения; в — угол отклонения маятника в момент времени t. Из этого уравнения свободного колебания маятника можно найти оценки интересующих характеристик. Аналогично, процессы в электрическом колебательном контуре описываются обыкновенным дифференциальным уравнением , где — индуктивность и емкость конденсатора; q(t) — заряд конденсатора в момент времени t. Из этого уравнения можно получить различные оценки характеристик процесса в колебательном контуре. Очевидно, что, введя обозначения , h1 = 0, , , получим обыкновенное дифференциальное уравнение второго порядка, описывающее поведение замкнутой системы: (5.3) где h0, hl, h2 — параметры системы; z(t) — состояние системы в момент времени t. Таким образом, поведение этих двух объектов может быть исследовано на основе общей математической модели (5.3). Кроме того, необходимо отметить, что поведение одной из систем может быть проанализировано с помощью другой. Например, поведение маятника (системы SM) может быть изучено с помощью электрического колебательного контура (системы SX). Если изучаемая система S, т. е. маятник или контур, взаимодействует с внешней средой Е, то появляется входное воздействие x(t) (внешняя сила для маятника и источник энергии для контура) и непрерывно-детерминированная модель такой системы будет иметь вид (5.4) С точки зрения общей схемы математической модели x(t) является входным (управляющим) воздействием, а состояние системы S в данном случае можно рассматривать как выходную характеристику, т. е. полагать, что выходная переменная совпадает с состоянием системы в данный момент времени y = z. При решении задач системотехники важное значение имеют проблемы управления большими системами. Следует обратить внимание на системы автоматического управления — частный случай динамических систем, описываемых D-схемами и выделенных в отдельный класс моделей в силу их практической специфики. Описывая процессы автоматического управления, придерживаются обычно представления реального объекта в виде двух систем: управляющей и управляемой (объекта управления). 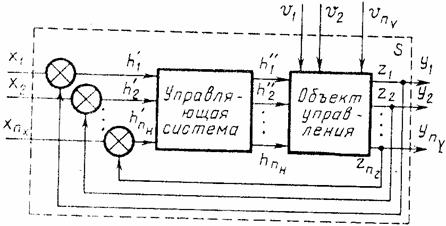Структура многомерной системы автоматического управления общего вида представлена на (рис. 3), где обозначены эндогенные переменные: — вектор входных (задающих) воздействий; — вектор возмущающих воздействий; — вектор сигналов ошибки; – вектор управляющих воздействий; независимые переменные: — вектор состояний системы S; — вектор выходныхпеременных, обычно . Рис 3. Структура системы автоматического управления Современная управляющая система — это совокупность программно-технических средств, обеспечивающих достижение объектом управления определенной цели. Насколько точно объект управления достигает заданной цели, можно судить для одномерной системы по координате состояния y(t). Разность между заданным yзад(t) и действительным y(t) законами изменения управляемой величины есть ошибка управления h'(t)= yзад(t) - y(t). Системы, для которых ошибки управления h'(t) = 0 во все моменты времени, называются идеальными. На практике реализация идеальных систем невозможна. Таким образом, ошибка h'(t) — необходимый субстрат автоматического управления, основанного на принципе отрицательной обратной связи, так как для приведения в соответствие выходной переменной у(t) ее заданному значению используется информация об отклонении между ними. Задачей системы автоматического управления является изменение переменной у(t) согласно заданному закону с определенной точностью (с допустимой ошибкой). При проектировании и эксплуатации систем автоматического управления необходимо выбрать такие параметры системы S, которые обеспечили бы требуемую точность управления, а также устойчивость системы в переходном процессе. Если система устойчива, то представляют практический интерес поведение системы во времени, максимальное отклонение регулируемой переменной у(t) в переходном процессе, время переходного процесса и т. п. Выводы о свойствах систем автоматического управления различных классов можно сделать по виду дифференциальных уравнений, приближенно описывающих процессы в системах. Порядок дифференциального уравнения и значения его коэффициентов полностью определяются статическими и динамическими параметрами системы S. Таким образом, использование D-схем позволяет формализовать процесс функционирования непрерывно-детерминированных систем S и оценить их основные характеристики, применяя аналитический или имитационный подход, реализованный в виде соответствующего языка для моделирования непрерывных систем или использующий аналоговые и гибридные средства вычислительной техники.