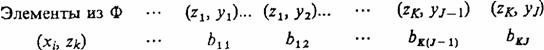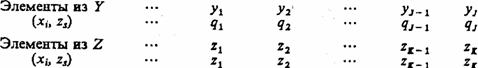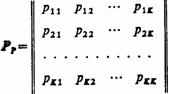ДИСКРЕТНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ (Р-схемы)

При дискретно-стохастическом подходе к формализации процесса функционирования системы S подход остается аналогичный рассмотренному конечному автомату, то влияние фактора стохастичности можно проследить разновидности таких автоматов, а именно на вероятностных (стохастических) автоматах.

В общем виде вероятностный автомат (англ. probabilistic automat) можно определить как дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически.

Применение схем вероятностных автоматов (Р - схем) имеет важное значение для разработки методов проектирования дискретных систем, проявляющих статистически закономерное случайное поведение, для выяснения алгоритмических возможностей таких систем и обоснования границ целесообразности их использования, а также для решения задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям.

множество G, элементами которого являются всевозможные пары , где хi и zs —-элементы входного подмножества X и подмножества состояний Z соответственно. Если существуют две такие функции j и y, то с их помощью осуществляются отображения  и , то говорят, что  определяет автомат детерминированного типа.

Введем в рассмотрение более общую математическую схему. Пусть Ф — множество всевозможных пар вида , где yj — элемент выходного подмножества Y. Потребуем, чтобы любой элемент множества G индуцировал на множестве Ф некоторый закон распределения следующего вида:

При этом , где bkj — вероятности перехода автомата в состояние zk и появления на выходе сигнала yj если он был в состоянии zs и на его вход в этот момент времени поступил сигнал xi. Число таких распределений, представленных в виде таблиц, равно числу элементов множества G. Обозначим множество этих таблиц через В. Тогда четверка элементов  называется вероятностным автоматом (Р - автоматом).

Пусть элементы множества G индуцируют некоторые законы распределения на подмножествах Y и Z, что можно представить соответственно в виде:

При этом  и  где zk и qk — вероятности перехода Р-автомата в состояние zk и появления выходного сигнала уk при условии, что Р-автомат находился в состоянии zs и на его вход поступил входной сигнал хi.

Если для всех k и j имеет место соотношение , то такой Р-автомат называется вероятностным автоматом Мили. Это требование означает выполнение условия независимости распределений для нового состояния Р-автомата и его выходного сигнала.

определение выходного сигнала Р-автомата зависит лишь от того состояния, в котором находится автомат в данном такте работы. Другими словами, пусть каждый элемент выходного подмножества Y индуцирует распределение вероятностей выходов, имеющее следующий вид:

Здесь , где si — вероятность появления выходного сигнала yi при условии, что Р-автомат находился в состоянии zk.

для всех k и i имеет место соотношение , то такой Р-автомат называется вероятностным автоматом Мура.

Понятие Р-автоматов Мили и Мура введено по аналогии с детерминированным F-автоматом, задаваемым . Частным случаем Р-автомата, задаваемого как  являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминированно. Если выходной сигнал Р-автомата определяется детерминированно, то такой автомат называется Y-детерминированным вероятностным автоматом. Аналогично, Z-детерминированным вероятностным автоматом называется Р-автомат, у которого выбор нового состояния является детерминированным.

Y-детерминированный Р-автомат задаётся таблицей переходов и таблицей выходов. Первую из этих таблиц можно представить в виде квадратной матрицы размерности К´К, которую будем называть матрицей переходных вероятностей или просто матрицей переходов Р-автомата. В общем случае такая матрица переходов имеет вид

Для описания Y-детерминированного Р-автомата необходимо задать начальное распределение вероятностей вида

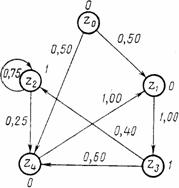
Здесь dk — вероятность того, что в начале работы Р-автомат находится в состоянии k. При этом .

Y-детерминированный Р-автомат можно задать в виде ориентированного графа, вершины которого сопоставляются состояниям автомата, а дуги — возможным переходам из одного состояния в другое. Дуги имеют веса, соответствующие вероятностям перехода рij, а около вершин графа пишутся значения выходных сигналов, индуцируемых этими состояниями рис 1.

рис 1.

Р-автоматы могут использоваться как генераторы марковских последовательностей, которые необходимы при построении и реализации процессов функционирования систем S или воздействий внешней среды Е.

Для оценки различных характеристик исследуемых систем, представляемых в виде Р-схем, кроме случая аналитических моделей можно применять и имитационные модели, реализуемые, например, методом статистического моделирования.