НЕПРЕРЫВНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ (Q-схемы)

При непрерывно-стохастическом подходе в качестве типовых математических схем применяется система массового обслуживания (англ. queueing system), которые будем называть Q-схемами. Системы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания.

В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования экономических, производственных, технических и других систем, например потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации ЭВМ от удаленных терминалов и т. д.

При этом характерным для работы таких объектов является случайное появление заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени, т. е. стохастический характер процесса их функционирования. Остановимся на основных понятиях массового обслуживания, необходимых для использования Q-схем, как при аналитическом, так и при имитационном.

В любом элементарном акте обслуживания можно выделить две основные составляющие:

1.    ожидание обслуживания заявки;

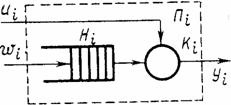
2.     собственно обслуживание заявки.

Это можно изобразить в виде некоторого i-гo прибора обслуживания Пi (рис. 2.), состоящего из накопителя заявок Нi, в котором может одновременно находиться  заявок, где  —емкость i-го накопителя, и канала обслуживания заявок (или просто канала) Ki

Рис. 2.

На каждый элемент прибора обслуживания Пi, поступают потоки событий: в накопитель Hi — поток заявок wi на канал Ki — поток обслуживания ui.

Потоком событий называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных событий.

Поток событий называется однородным, если он характеризуется только моментами поступления этих событий (вызывающими моментами) и задается последовательностью , где tn — момент наступления n-го события — неотрицательное вещественное число.

Однородный поток событий также может быть задан в виде последовательности промежутков времени между n-м и (n—1)-м событиями {tn}, которая однозначно связана с последовательностью вызывающих моментов {tn}, где ,, to = 0, т. е. t1 = t1

Потоком неоднородных событий называется последовательность , где tn — вызывающие моменты; fn — набор признаков события. Например, применительно к процессу обслуживания для неоднородного потока заявок могут быть заданы принадлежность к тому или иному источнику заявок, наличие приоритета, возможность обслуживания тем или иным типом канала и т. п.

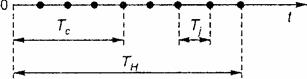
поток, в котором события разделены интервалами времени t1, t2,…, которые вообще являются случайными величинами. Пусть интервалы t1, t2,.., независимы между собой. Тогда поток событий называется потоком с ограниченным последействием. Пример потока событий приведен на рис. 3. , где обозначено Тj — интервал между событиями (случайная величина); Тн — время наблюдения, Tс — момент совершения события.

рис. 3.

Интенсивность потока можно рассчитать экспериментально по формуле

где N— число событий, произошедших за время наблюдения Тн. Если         Тн =const или определено какой-либо формулой , то поток называется детерминированным. Иначе поток называется случайным.

Случайные потоки бывают:

1.               ординарными - когда вероятность одновременного появления 2-х и более событий равна нулю. Поток событий называется ординарным, если вероятность того, что на малый интервал времени Dt, примыкающий к моменту времени t, попадает больше одного события Р>1 (t, Dt), пренебрежительно мала по сравнению с вероятностью того, что на этот же интервал времени Dt попадает ровно одно событие P1 (t, Dt), т. е. P1 (t, Dt)» Р>1 (t, Dt).

2.               стационарными - когда частота появления событий постоянная. Стационарным потоком событий называется поток, для которого вероятность появления того или иного числа событий на интервале времени t зависит лишь от длины этого участка и не зависит от того, где на оси времени  взят этот участок.

3.               без последействия - когда вероятность не зависит от момента совершения предыдущих событий.

Обычно при моделировании различных систем применительно к элементарному каналу обслуживания Кi можно считать, что поток заявок , т. е. интервалы времени между моментами появления заявок (вызывающие моменты) на входе Ki образует подмножество неуправляемых переменных, а поток обслуживания , т. е. интервалы времени между началом и окончанием обслуживания заявки, образует подмножество управляемых переменных.

Заявки, обслуженные каналом Кi и заявки, покинувшие прибор Пi, по различным причинам необслуженными (например, из-за переполнения накопителя Нi), образуют выходной поток , т. е. интервалы времени между моментами выхода заявок образуют подмножество выходных переменных.

В практике моделирования систем, имеющих более сложные структурные связи и алгоритмы поведения, для формализации используются не отдельные приборы обслуживания, а Q-схемы, образуемые композицией многих элементарных приборов обслуживания Пi ( (сети массового обслуживания). Если каналы Кi различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема), а если приборы Пi и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема). Таким образом, для задания Q-схемы необходимо использовать оператор сопряжения R, отражающий взаимосвязь элементов структуры (каналов и накопителей) между собой. Связи между элементами Q-схемы изображают в виде стрелок (линий потока, отражающих направление движения заявок). Различают разомкнутые и замкнутые Q-схемы.

В разомкнутой Q-схеме выходной поток обслуженных заявок не может снова поступить на какой-либо элемент, т. е. обратная связь отсутствует.

В замкнутых Q-схемах имеются обратные связи, по которым заявки двигаются в направлении, обратном движению вход-выход.

Для задания Q-схемы также необходимо описать алгоритмы ее функционирования, которые определяют набор правил поведения заявок в системе в различных неоднозначных ситуациях. В зависимости от места возникновения таких ситуаций различают алгоритмы (дисциплины) ожидания заявок в накопителе Нi, и обслуживания заявок каналом Кi каждого элементарного обслуживающего прибора Пi Q-схемы. Неоднородность заявок, отражающая процесс в той или иной реальной системе, учитывается с помощью введения классов приоритетов.

В зависимости от динамики приоритетов в Q-схемах различают статические и динамические приоритеты.

Статические приоритеты назначаются заранее и не зависят от состояний Q-схемы, т. е. они являются фиксированными в пределах решения конкретной задачи моделирования.

Динамические приоритеты возникают при моделировании в зависимости от возникающих ситуаций.

Исходя из правил выбора заявок из накопителя Hi на обслуживание каналом Кi можно выделить относительные и абсолютные приоритеты.

Относительный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель Нi ожидает окончания обслуживания предшествующей заявки каналом Кi и только после этого занимает канал.

Абсолютный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель Нi прерывает обслуживание каналом Кi заявки с более низким приоритетом и сама занимает канал (при этом вытесненная из Кi заявка может либо покинуть систему, либо может быть снова записана на какое-то место в Нi).

При рассмотрении алгоритмов функционирования приборов обслуживания Пi (каналов Кi и накопителей Нi) необходимо также задать набор правил, по которым заявки покидают Нi и Кi, для Нi — либо правила переполнения, по которым заявки в зависимости от заполнения Нi, покидают систему, либо правила ухода, связанные с истечением времени ожидания заявки в Нi, для Кi — правила выбора маршрутов или направлений ухода.

Кроме того, для заявок необходимо задать правила, по которым они остаются в канале Кi или не допускаются до обслуживания каналом Кi т. е. правила блокировок канала. При этом различают блокировки Кi по выходу и по входу.

Весь набор возможных алгоритмов поведения заявок в Q-схеме можно представить в виде некоторого оператора алгоритмов поведения заявок А.

Таким образом, Q-схема, описывающая процесс функционирования системы массового обслуживания любой сложности, однозначно задается в виде .

При ряде упрощающих предположений относително подмножеств входящих потоков W и потоков обслуживания U (выполнение условий стационарности, ординарности и ограниченного последействия) оператора сопряжения элементов структуры R (однофазное одноканальное обслуживание в разомкнутой системе), подмножества собственных параметров Н (обслуживание с бесконечной емкостью накопителя), оператора алгоритмов обслуживания заявок А (бесприоритетное обслуживание без прерываний и блокировок) для оценки вероятностно-временных характеристик можно использовать аналитический аппарат, разработанный в теории массового обслуживания.