Сетевые модели (N-схемы)

В практике моделирования объектов часто приходится решать задачи, связанные с формализованным описанием и анализом причинно-следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов. Самым распространенным в настоящее время формализмом, описывающим структуру и взаимодействие параллельных систем и процессов, являются сети Петри (англ. Petri Nets), предложенные К. Петри. Теория сетей Петри развивается в нескольких направлениях: 1. разработка математических основ, 2. структурная теория сетей, 3. различные приложения (параллельное программирование, дискретные динамические системы и т. д.). Формально сеть Петри (N-схема) задается четверкой вида , где В — конечное множество символов, называемых позициями , D — конечное множество символов, называемых переходами, , ; I — входная функция (прямая функция инцидентности) ; О — выходная функция (обратная функция инцидентности), . Таким образом, входная функция I отображает переход dj в множество входных позиций , а выходная функция О отображает переход dj в множество выходных позиций . Для каждого перехода можно определить множество входных позиций перехода I(dj) и выходных позиций перехода О(dj) как Аналогично, для каждого перехода вводятся определения множества входных переходов позиции I(bi) и множества выходных переходов позиции O(bi): . 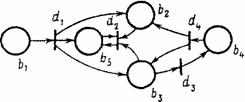Графически N-схема изображается в виде двудольного ориентированного мультиграфа, представляющего собой совокупность позиций и переходов (рис. 1). Рис. 1. Графическое изображение N-схемы Как видно из этого рисунка, граф N-схемы имеет два типа узлов: позиции и переходы, изображаемые 0 и 1 соответственно. Ориентировочные дуги соединяют позиции и переходы, причем каждая дуга направлена от элемента одного множества (позиции или перехода) к элементу другого множества (переходу или позиции). Граф N-схемы является мультиграфом, так как он допускает существование кратных дуг от одной вершины к другой. Приведенное представление N-схемы может использоваться только для отражения статики моделируемой системы (взаимосвязи событий и условий), но не позволяет отразить в модели динамику функционирования моделируемой системы. Для представления динамических свойств объекта вводится функция маркировки (разметки) . Маркировка М есть присвоение неких абстрактных объектов, называемых метками (фишками), позициям N-схемы, причем количество меток, соответствующее каждой позиции, может меняться. При графическом задании N-схемы разметка отображается помещением внутри вершин-позиций соответствующего числа точек (когда количество точек велико, ставят цифры). Маркированная (размеченная) N-схема может быть описана в виде пятерки и является совокупностью сети Петри и маркировки М. 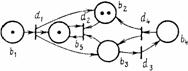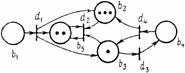Функционирование N-схемы отражается путем перехода от разметки к разметке. Начальная разметка обозначается как . Смена разметок происходит в результате срабатывания одного из переходов сети. Необходимым условием срабатывания перехода dj является , где , - разметка позиции bi. Переход dj для которого выполняется указанное условие, определяется как находящийся в состоянии готовности к срабатыванию или как возбужденный переход. Срабатывание перехода изменяет разметку сети М(b) = (М(b1), М(b2), ..., M(bn))2 на разметку М¢(b) по следующему правилу: M'(b) = M(b)-I(dj) + O(dj) т. е. переход dj изымает по одной метке из каждой своей входной позиции и добавляет по одной метке в каждую из выходных позиций. Рис. 2. Пример функционирования размеченной N-схемы Важной особенностью моделей процесса функционирования систем с использованием типовых N-схем является простота построения иерархических конструкций модели. С одной стороны, каждая N-схема может рассматриваться как макропереход или макропозиция модели более высокого уровня. С другой стороны, переход, или позиция N-схемы, может детализироваться в форме отдельной подсети для более углубленного исследования процессов в моделируемой системе S. Типовые N-схемы на основе обычных размеченных сетей Петри пригодны для описания в моделируемой системе S событий произвольной длительности. В этом случае модель, построенная с использованием таких N-схем, отражает только порядок наступления событий в исследуемой системе S. Для отражения временных параметров процесса функционирования моделируемой системы S на базе N-схем используется расширение аппарата сетей Петри: временные сети, E-сети.
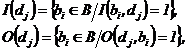
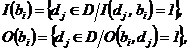