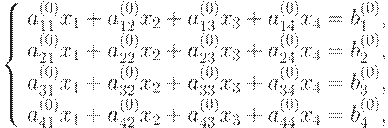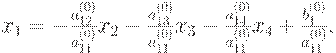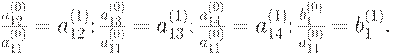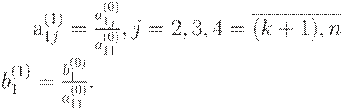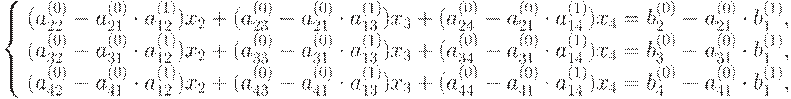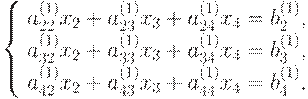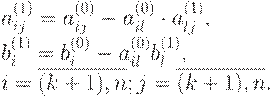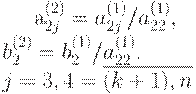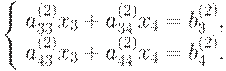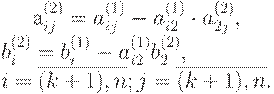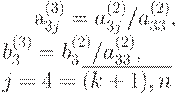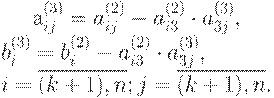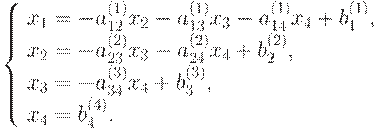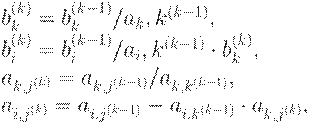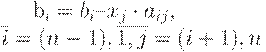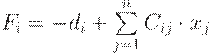Решение систем линейных уравнений методом Гаусса

Метод Гаусса является точным методом. Он позволяет получить решение системы за конечное число арифметических действий. В основе метода лежит идея последовательного исключения неизвестных. Метод состоит из двух этапов. На первом этапе (прямой ход) система при помощи последовательного исключения неизвестных приводится к треугольному виду. На втором этапе (обратный ход) из системы треугольного вида последовательно, в обратном порядке, начиная c n-го уравнения, находятся неизвестные системы.

В качестве примера возьмем систему 4 порядка.

$Описание: Описание: \left\{ \begin{array}{l} a_{11}^{(0)}x_1 + a_{12}^{(0)}x_2 + a_{13}^{(0)}x_3 + a_{14}^{(0)}x_4 = b_1^{(0)},\\ a_{21}^{(0)}x_1 + a_{22}^{(0)}x_2 + a_{23}^{(0)}x_3 + a_{24}^{(0)}x_4 = b_2^{(0)},\\ a_{31}^{(0)}x_1 + a_{32}^{(0)}x_2 + a_{33}^{(0)}x_3 + a_{34}^{(0)}x_4 = b_3^{(0)},\\ a_{41}^{(0)}x_1 + a_{42}^{(0)}x_2 + a_{43}^{(0)}x_3 + a_{44}^{(0)}x_4 = b_4^{(0)}, \end{array} \right.$

( 9.1)

Прямой ход. На первом шаге прямого хода (к=1) находим x1 из первого уравнения системы (9.1).

$Описание: Описание: a_{11}^{(0)}$ - ведущий элемент первой строки.

Если $Описание: Описание: a_{11}^{(0)} \neq 0$ , то

$Описание: Описание: x_1= - \frac {a_{12}^{(0)}}{a_{11}^{(0)}} x_2 - \frac {a_{13}^{(0)}}{a_{11}^{(0)}} x_3 - \frac {a_{14}^{(0)}}{a_{11}^{(0)}} x_4 + \frac {b_1^{(0)}}{a_{11}^{(0)}},$

( 9.2)

Обозначим:

$Описание: Описание: \frac {a_{12}^{(0)}}{a_{11}^{(0)}} = a_{12}^{(1)}; \frac {a_{13}^{(0)}}{a_{11}^{(0)}} = a_{13}^{(1)}; \frac {a_{14}^{(0)}}{a_{11}^{(0)}} = a_{14}^{(1)}; \frac {b_1^{(0)}}{a_{11}^{(0)}} = b_1^{(1)}.$

( 9.3)

Подставляя (9.3) в (9.2), получим

$Описание: Описание: x_1 = -a_{12}^{(1)}x_2 - a_{13}^{(1)}x_3 - a_{14}^{(1)}x_4 + b_1^{(1)},$

( 9.4)

где

$Описание: Описание: a_{1j}^{(1)} = \frac{a_{1j}^{(0)}}{a_{11}^{(0)}}, j=2,3,4 = \overline{(k+1),n}\\ b_1^{(1)} = \frac{b_1^{(0)}}{a_{11}^{(0)}}.$

Подставляем (9.4) во 2, 3 и 4 уравнение системы (9.1), получим:

$Описание: Описание: \left\{ \begin{array}{l} (a_{22}^{(0)} - a_{21}^{(0)} \cdot a_{12}^{(1)}) x_2 + (a_{23}^{(0)} - a_{21}^{(0)} \cdot a_{13}^{(1)}) x_3 + (a_{24}^{(0)} - a_{21}^{(0)} \cdot a_{14}^{(1)}) x_4 = b_2^{(0)} - a_{21}^{(0)}\cdot b_1^{(1)},\\ (a_{32}^{(0)} - a_{31}^{(0)} \cdot a_{12}^{(1)}) x_2 + (a_{33}^{(0)} - a_{31}^{(0)} \cdot a_{13}^{(1)}) x_3 + (a_{34}^{(0)} - a_{31}^{(0)} \cdot a_{14}^{(1)}) x_4 = b_3^{(0)} - a_{31}^{(0)}\cdot b_1^{(1)},\\ (a_{42}^{(0)} - a_{41}^{(0)} \cdot a_{12}^{(1)}) x_2 + (a_{43}^{(0)} - a_{41}^{(0)} \cdot a_{13}^{(1)}) x_3 + (a_{44}^{(0)} - a_{41}^{(0)} \cdot a_{14}^{(1)}) x_4 = b_4^{(0)} - a_{41}^{(0)}\cdot b_1^{(1)}, \end{array} \right.$

Обозначив коэффициенты при неизвестных полученной системы через $Описание: Описание: a_{ij}^{(1)}$ , а свободные члены через $Описание: Описание: b_i^{(1)}$ перепишем полученную систему:

$Описание: Описание: \left\{ \begin{array}{l} a_{22}^{(1)} x_2 + a_{23}^{(1)} x_3 + a_{24}^{(1)} x_4 = b_2^{(1)},\\ a_{32}^{(1)} x_2 + a_{33}^{(1)} x_3 + a_{34}^{(1)} x_4 = b_3^{(1)},\\ a_{42}^{(1)} x_2 + a_{43}^{(1)} x_3 + a_{44}^{(1)} x_4 = b_4^{(1)}. \end{array} \right.$

( 9.5)

где

$Описание: Описание: a_{ij}^{(1)} = a_{ij}^{(0)} - a_{il}^{(0)} \cdot a_{lj}^{(1)},\\ b_i^{(1)} =b_i^{(0)} -a_{il}^{(0)} b_l^{(1)},\\ i=\overline{(k+1),n}; j=\overline{(k+1),n}.$

Таким образом, в результате выполнения первого шага прямого хода исходная система (9.1) n-го порядка преобразована к совокупности уравнения (9.4) и системы линейных уравнений (9.5), порядок которой равен n-1.

На втором шаге прямого хода (к=2) из первого уравнения системы (9.5) находим x2.

$Описание: Описание: a_{22}^{(1)}$ -ведущий элемент первой строки системы (9.5).

Если $Описание: Описание: a_{22}^{(1)} \neq 0$ , то из первого уравнения системы (9.5) имеем:

$Описание: Описание: x_2= - a_{23}^{(2)}x_3 - a_{24}^{(2)}x_4 + b_2^{(2)},$

( 9.6)

где

$Описание: Описание: a_{2j}^{(2)} = a_{2j}^{(1)}/ a_{22}^{(1)},\\ b_2^{(2)} = b_2^{(1)}/ a_{22}^{(1)}.\\ j=3,4=\overline{(k+1),n}$

Подставив выражение (9.6) во второе и третье уравнения системы (9.5), получим новую систему линейных уравнений, порядок которой равен n-2.

$Описание: Описание: \left\{ \begin{array}{l} a_{33}^{(2)}x_3 + a_{34}^{(2)}x_4 = b_3^{(2)},\\ a_{43}^{(2)}x_3 + a_{44}^{(2)}x_4 = b_4^{(2)}. \end{array} \right.$

( 9.7)

где

$Описание: Описание: a_{ij}^{(2)} = a_{ij}^{(1)} - a_{i2}^{(1)} \cdot a_{2j}^{(2)}, \\b_i^{(2)} = b_i^{(1)} - a_{i2}^{(1)}b_2^{(2)},\\ i=\overline{(k+1),n}; j=\overline{(k+1),n}.$

Таким образом, в результате выполнения второго шага прямого хода исходная система (9.1) преобразована к совокупности уравнений (9.4), (9.6) и системы линейных уравнений (9.7),порядок которой равен n-2.

На третьем шаге прямого хода (к=3) из системы (9.7) находим x3.

$Описание: Описание: a_{33}^{(2)}$ - ведущий элемент системы (9.7).

Если $Описание: Описание: a_{33}^{(2)} \neq 0$ , то из первого уравнения системы (9.7) имеем:

$Описание: Описание: x_3= -a_{34}^{(3)}x_4 + b_3^{(3)},$

( 9.8)

где

$Описание: Описание: a_{3j}^{(3)} = a_{3j}^{(2)}/ a_{33}^{(2)},\\ b_3^{(3)} = b_3^{(2)}/ a_{33}^{(2)},\\ j=4=\overline{(k+1),n}$

Подставив выражение (9.8) для x3 во второе уравнение системы (9.7) получим:

$Описание: Описание: a_{44}^{(3)}x_4 = b_4^{(3)},$

( 9.9)

где

$Описание: Описание: a_{ij}^{(3)} = a_{ij}^{(2)} - a_{i3}^{(2)} \cdot a_{3j}^{(3)},\\ b_i^{(3)} = b_i^{(2)} - a_{i3}^{(2)} \cdot a_{3j}^{(3)},\\ i=\overline{(k+1),n}; j=\overline{(k+1),n}.$

На последнем шаге прямого хода, если $Описание: Описание: a_{44}^{(3)} \neq 0,$ то из уравнения (9.9) имеем:

$Описание: Описание: x_4 = b_4^{(4)},$

( 9.10)

где

$Описание: Описание: b_4^{(4)} = b_4^{(3)}/ a_{44}^{(3)}.$

( 9.11)

В результате выполнения всех шагов прямого хода исходная система (9.1) приводится к системе треугольного вида, полученной объединением уравнений (9.4), (9.6), (9.8), (9.10):

$Описание: Описание: \left\{ \begin{array}{l} x_1= -a_{12}^{(1)}x_2 - a_{13}^{(1)}x_3 - a_{14}^{(1)}x_4 + b_1^{(1)},\\ x_2= -a_{23}^{(2)}x_3 - a_{24}^{(2)}x_4 + b_2^{(2)},\\ x_3= -a_{34}^{(3)}x_4 + b_3^{(3)},\\ x_4= b_4^{(4)}. \end{array} \right.$

( 9.12)

При построении алгоритма прямого хода вычисление организуем в цикле по шагам, т.е. $Описание: Описание: k=\overline{1,(n-1)}$ .

Последний n-й шаг прямого хода выведем из цикла т.к. здесь реализуется только одно вычисление

$Описание: Описание: b_n=\frac{b_n}{a_{nn}}.$

( 9.13)

В процессе выполнения всех шагов прямого хода все преобразования коэффициентов и свободных членов проводим по полученным ранее рекуррентным формулам:

$Описание: Описание: b_k^{(k)}= b_k^{(k-1)}/a_k,k^{(k-1)},\\ b_i^{(k)}= b_i^{(k-1)}/a_i,k^{(k-1)} \cdot b_k^{(k)},\\ a_{k,j^{(k)}}= a_{k,j^{(k-1)}}/a_{k,k^{(k-1)}},\\ a_{i,j^{(k)}}= a_{i,j^{(k-1)}}-a_{i,k^{(k-1)}} \cdot a_{k,j^{(k)}},$

( 9.14)

где

$Описание: Описание: k=\overline{1,(n-1)}$ – номер шага прямого хода,

$Описание: Описание: i=\overline{(k+1),n}$ - номер уравнения систем (9.5), (9.7)

$Описание: Описание: j=\overline{(k+1),n}$

В процессе обратного хода из системы (9.12) неизвестные находятся в обратном порядке. Значение корня х4 находят из последнего уравнения системы (9.12). Далее х4 используется для отыскания корня х3 из 3-го уравнения, далее х3 и х4 используются отыскания х2 из 2-го уравнения системы (9.12), и, наконец, х2, х3 и х4 используются для отыскания х1 из 1-го уравнения системы (9.12).

Все вычисления обратного хода проводим в цикле по i, где

$Описание: Описание: i=\overline{(n-1)},1$ по рекуррентным формулам:

$Описание: Описание: b_i={b_i – x_j \cdot a_{ij}} , \\ \overline i=(n-1),\overline {1,j}=(i+1),n$

xi= bi.

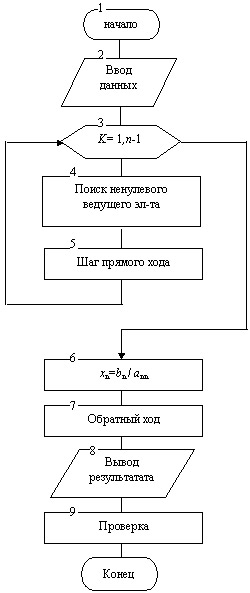
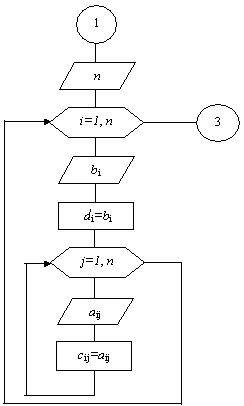
Рассмотренный выше простейший вариант метода Гаусса, называемый схемой единственного деления, обладает следующим недостатком: если ведущий элемент akk какой-либо строки окажется равным нулю, то этот метод формально непригоден, хотя система может иметь единственное решение. Из этих соображений в схеме алгоритма добавлен поиск ненулевого ведущего элемента.

На рисунке 9.1 представлена укрупнённая схема алгоритма (блок-схема) метода Гаусса. На рисунках 9.2 - 9.6 представлены алгоритмы отдельных блоков метода.

Описание: Описание: Укрупнённая схема алгоритма (блок-схема) метода Гаусса

Рис. 9.1. Укрупнённая схема алгоритма (блок-схема) метода Гаусса

Блок 2. С помощью двух вложенных циклов с управляющими переменными i=1,n и j=1,k организуем ввод коэффициентов ai,j и свободных членов bi исходной системы. Для того, чтобы в дальнейшем можно было выполнить в блоке 9 проверку результата, в алгоритме предусмотрено сохранение значений ai,j и bi исходной системы с помощью переприсвоений: cij=aij и di=bi

Описание: Описание:

Рис. 9.2.

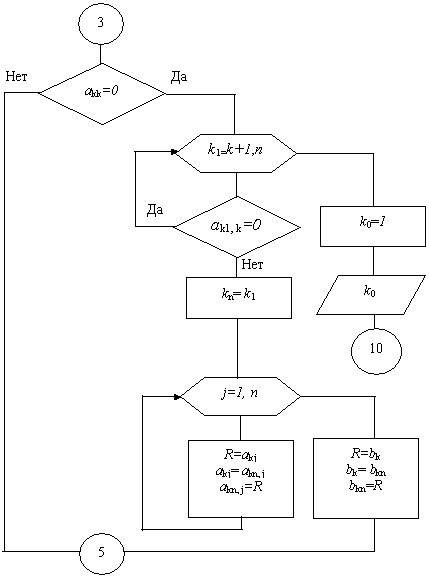
Блок 3. Организуем цикл по k, внутри которого производится вычисление по всем шагам прямого хода. Последний п-й шаг прямого хода выводим из цикла.

Блок 4. На каждом шаге прямого хода выполняем поиск ненулевого ведущего элемента.

Описание: Описание:

Рис. 9.3.

Поиск ненулевого ведущего элемента ведётся в следующем порядке:

а) На каждом k-ом шаге прямого хода ведущий элемент каждой строки сравнивается с нулём;

б) Если в k-ой строке имеется нулевой ведущий элемент, то в k-ом столбце в цикле осуществляется поиск ненулевого элемента.

в) Если в какой-то строке kn такой ненулевой элемент найден, то строки kn и k поэлементно, в цикле по k1=(k+1),n, меняем местами. Для перестановки элементов используется рабочая переменная R.

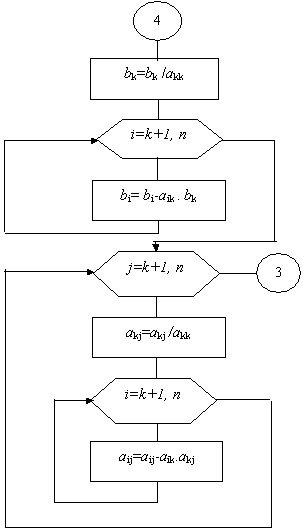
г) Если ненулевой ведущий элемент не найден, то коду ошибки kо присваиваем значение 1 и расчёт прекращается.

Блок 5 - шаг прямого хода. На каждом шаге прямого хода проводим исключение неизвестных путём преобразования коэффициентов и свободных членов системы по полученным ранее рекуррентным формулам.

Описание: Описание:

Рис. 9.4.

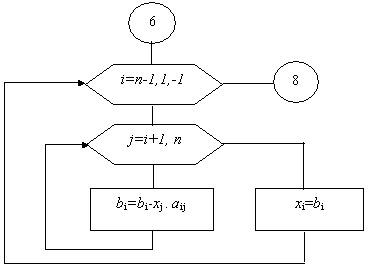
Блок 6. В этом блоке выведем из цикла по k последний шаг прямого хода, т.к. на этом шаге не нужны преобразования коэффициентов и свободных членов, а реализуется только одно вычисление

xn=bn/an,n

Блок 7 - обратный ход. В процессе обратного хода метода Гаусса из системы треугольного вида последовательно в обратном порядке в цикле по i=(n-1),1,-1 находим неизвестные системы по рекуррентной формуле

bi= bi - xj.ai,j , i=(n-1),1, j=(n+1),n.

При этом в цикле по j=(i+1),n использован приём последовательного вычитания xj.ai,j из bi,после чего вводится переприсвоение bi =хi.

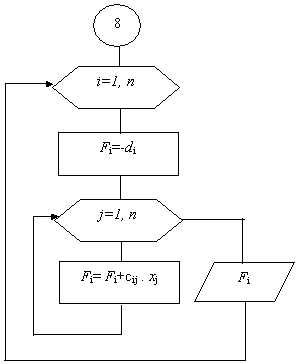
Описание: Описание:

Рис. 9.5.

Блок 9 - проверка результата. В этом блоке подставляя значения полученных неизвестных в исходную систему и используя сохранённые значения коэффициентов системы ci,j и свободных членов di, проводим проверку решения задачи по формуле

$Описание: Описание: F_i = -d_i + \sum \limits_{j=1}^{n}C_{ij} \cdot x_j$

Если корни системы найдены, то Fi – это число, близкое к нулю.

Блок 9 в алгоритме метода Гаусса рекомендуется использовать только в процессе отладки метода.

В дальнейшем, при использовании метода Гаусса при решении различных прикладных задач, особенно в тех случаях, когда метод Гаусса используется внутри другого метода, блок 9 можно опустить, а в блоке 2 при вводе данных исходные значения коэффициентов системы и её свободных членов можно не сохранять.

Описание: Описание:

Рис. 9.6.