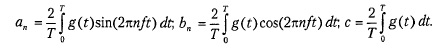5. Физичесий уровень

Информация может передаваться по проводам за счет изменения какой-либо физической величины, например напряжения или силы тока. Представив значение напряжения или силы тока в виде однозначной функции времени g(t), мы сможем смоделировать поведение сигнала и подвергнуть его математическому анализу. Этому анализу и посвящены следующие разделы.

В начале XIX столетия французский математик Жан Батист Фурье (Jean Baptiste Fourier) доказал, что любая периодическая функция g (t) с периодом Т может быть разложена в ряд (возможно, бесконечный), состоящий из сумм синусов и косинусов:

Где f = 1/Т – основная частота (гармоника), аn и bn – амплитуды синусов и косинусов n-й гармоники, а с – константа. Подобное разложение называется рядом Фурье. Разложенная в ряд Фурье функция может быть восстановлена по элементам этого ряда, то есть если период Т и амплитуды гармоник известны, то исходная функция может быть восстановлена с помощью суммы ряда (2.1).

Информационный сигнал, имеющий конечную длительность (все информационные сигналы имеют конечную длительность), может быть разложен в ряд Фурье, если представить, что весь сигнал бесконечно повторяется снова и снова (то есть интервал от T до 2T полностью повторяет интервал от 0 до T, и т. д.).

Амплитуды аn могут быть вычислены для любой заданной функции g(t). Для этого нужно умножить левую и правую стороны уравнения на sin (2πkft), а затем проинтегрировать от 0 до Т. Поскольку:

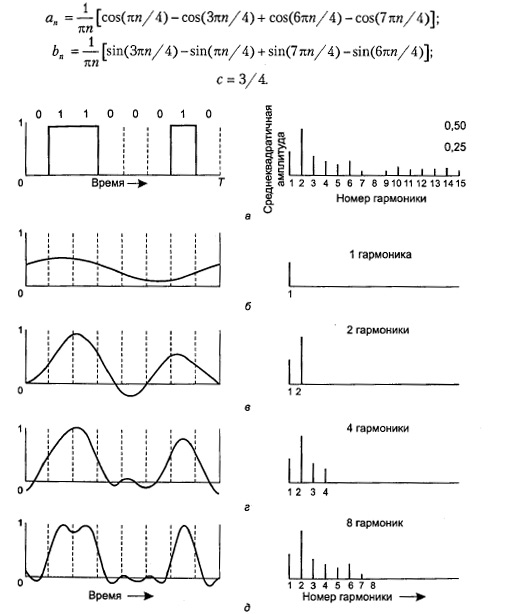
остается только один член ряда: an. Ряд bn исчезает полностью. Аналогично, умножая уравнение (2.1) на cos (2πkft) и интегрируя по времени от 0 до Т, мы можем вычислить значения bn. Если проинтегрировать обе части уравнения, не изменяя его, то можно получить значение константы с. Результаты этих действий будут следующими:

5.2 Сигналы с ограниченным спектром

Чтобы понять, какое отношение все вышеизложенное имеет к передаче данных, рассмотрим конкретный пример – передачу двоичного кода ASCII символа «b». Для этого потребуется 8 бит (то есть 1 байт). Задача – передать следующую последовательность бит: 01100010. На рис. слева изображена зависимость выходного напряжения от времени на передающем компьютере. В результате анализа Фурье для данного сигнала получаем следующие значения коэффициентов:

Среднеквадратичные амплитуды для нескольких первых гармоник показаны на рис. справа. Эти значения представляют интерес, поскольку их квадраты пропорциональны энергии, передаваемой на соответствующей частоте.

Ни один канал связи не может передавать сигналы без потери мощности. Если бы все гармоники ряда Фурье уменьшались при передаче в равной степени, то сигнал уменьшался бы по амплитуде, но не искажался (то есть у него была бы та же самая замечательная прямоугольная форма, как на рис. а). К сожалению, все каналы связи уменьшают гармоники ряда Фурье в разной степени, тем самым искажая передаваемый сигнал. Как правило, амплитуды передаются без уменьшения в частотном диапазоне от 0 до некоей частоты 1/с (измеряемой в периодах в секунду или герцах (Гц)), при этом высокочастотная составляющая сигнала (выше частоты 1/с, называемой частотой среза) заметно ослабляется. Этот диапазон частот называется полосой пропускания. На практике срез вовсе не является таким резким, поэтому обычно в упомянутую полосу пропускания включают те частоты, которые передаются с потерей мощности, не превышающей 50 %.

Полоса пропускания является физической характеристикой среды передачи данных и зависит обычно от конструкции, толщины и длины носителя. Иногда для намеренного уменьшения полосы пропускания, доступной абонентам, в линию включается специальное устройство – фильтр. Например, кабель, используемый в телефонии при небольших расстояниях, имеет полосу пропускания, равную 1 МГц, однако телефонные компании с помощью частотных фильтров урезают ее, предоставляя пользователям лишь 3100 Гц. Такой полосы, впрочем, вполне хватает для отчетливой передачи речи, зато за счет уменьшения расходуемых каждым абонентом ресурсов повышается общая эффективность системы.

Теперь посмотрим, как будет выглядеть сигнал, изображенный на рис., если полоса пропускания канала будет такой, что через него будут проходить только самые низкие частоты (то есть функция g(t) будет аппроксимирована лишь несколькими первыми членами рядов уравнения (2.1)). На рис. 2.1, б показан сигнал на выходе канала, пропускающего лишь первую (основную, f) гармонику сигнала. Аналогично, рис. 2.1, вд показывают спектры и восстановленные сигналы для каналов с более широкой полосой пропускания.

При заданной скорости передачи в битах, равной b бит/с, время, требуемое для передачи, скажем, 8 бит, будет равно 8/b секунд. Таким образом, частота первой гармоники равна b/8 Гц. Обычная телефонная линия, часто называемая речевым каналом, имеет искусственно созданную частоту среза около 3000 Гц. 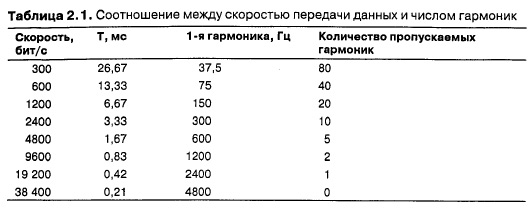Это ограничение означает, что номер самой высокой гармоники, прошедшей сквозь телефонный канал, примерно (срез не очень крутой) равен 3000/(6/8) или 24 000/6.

Для некоторых скоростей передачи данных эти значения показаны в табл. 2.1. Из приведенных данных ясно, что попытка передать по речевому каналу данные на скорости 9600 бит/с превратит сигнал, показанный на рис. 2.1, а, в нечто подобное рис. 2.1, в, что сделает прием исходного потока битов с приемлемым качеством практически невозможным. Очевидно, что у сигналов, передаваемых со скоростью 38 400 бит/с и выше, нет никаких шансов пройти через речевой канал, Даже при полном отсутствии помех на линии. Другими словами, ограничение полосы пропускания частот канала ограничивает его пропускную способность для передачи двоичных данных, даже для идеальных каналов. Однако схемы, использующие несколько уровней напряжений, существуют и позволяют достичь более высоких скоростей передачи данных.

5.3 Максимальная скорость передачи данных через канал

В 1924 году американский ученый X. Найквист (Н. Nyquist) из компании AT&T пришел к выводу, что существует некая предельная скорость передачи даже для идеальных каналов. Он вывел уравнение, позволяющее найти максимальную скорость передачи данных в бесшумном канале с ограниченной полосой пропускания частот. В 1948 году Клод Шеннон (Claude Shannon) продолжил работу Найквиста и расширил ее для случая канала со случайным (то есть термодинамическим) шумом. Мы кратко рассмотрим результаты работы Найквиста и Шеннона, ставшие сегодня классическими.

Найквист доказал, что если произвольный сигнал прошел через низкочастотный фильтр с полосой пропускания Я, то такой отфильтрованный сигнал может быть полностью восстановлен по дискретным значениям этого сигнала, измеренным с частотой 2Я в секунду. Производить измерения сигнала чаще, чем 2# в секунду, нет смысла, так как более высокочастотные компоненты сигнала были отфильтрованы. Если сигнал состоит из V дискретных уровней, то уравнение Найквиста будет выглядеть так:

максимальная скорость передачи данных = 2H log₂ V, бит/с

Так, например, бесшумный канал с частотой пропускания в 3 кГц не может передавать двоичные (то есть двухуровневые) сигналы на скорости, превосходящей 6000 Кбит/с.

Итак, мы рассмотрели случай бесшумных каналов. При наличии в канале случайного шума ситуация резко ухудшается. Уровень термодинамического шума в канале измеряется отношением мощности сигнала к мощности шума и называется отношением сигнал/шум. Если обозначить мощность сигнала S, а мощность шума – N, то отношение сигнал/шум будет равно S/N. Обычно сама величина отношения не употребляется. Вместо нее используется ее десятичный логарифм, умноженный на 10: 10 lg S/N. Такая единица называется децибелом (decibel, dB, дБ). Таким образом, если отношение сигнал/шум 10, это соответствует 10 дБ, отношение 100 равно 20 дБ, отношение 1000 равно 30 дБ и т. д. Производители стереоусилителей часто указывают полосу частот (частотный диапазон), в котором их аппаратура имеет линейную амплитудночастотную характеристику в пределах 3 дБ. Отклонение в 3 дБ соответствует ослаблению сигнала примерно в два раза (потому что log₁₀3 = 0,5).

Главным результатом, который получил Шеннон, было утверждение о том, что максимальная скорость передачи данных в канале с полосой частот F Гц и отношением сигнал/шум, равным S/N, можно вычислить по формуле

максимальная скорость передачи данных = F log₂(l+S/N).

Например, канал с частотной полосой пропускания в 3000 Гц и отношением мощностей сигнала и термального шума в 30 дБ (обычные параметры для аналоговой части телефонной системы) никогда не сможет передавать более 30 000 бит/с, независимо от способа модуляции сигнала, то есть количества используемых уровней сигнала, частоты дискретизации и т. д. Результат, полученный Шенноном и подкрепленный постулатами теории информации, применим к любому каналу с гауссовским (термальным) шумом. Попытки доказать обратное следует считать обреченными не провал. Однако следует заметить, что данная теорема описывает верхний, теоретический предел пропускной способности информационного канала, и реальные системы редко достигают его.

ЗАДАЧА

1. По бесшумному каналу с полосой пропускания 4 кГц каждую 1 мс передаются отсчеты сигнала. Какова будет максимальная скорость передачи данных?

A noiseless channel can carry an arbitrarily large amount of information, no matter how often it is sampled. Just send a lot of data per sample. For the 4 kHz channel, make 8000 samples/sec. If each sample is 16 bits, the channel can send 128 kbps. If each sample is 1024 bits, the channel can send 8.2 Mbps. The key word here is ‘‘noiseless.’’ With a normal 4 kHz channel, the Shannon limit would not allow this.

2. Ширина телевизионных каналов составляет 6 МГц. Сколько бит в секунду может быть передано по такому каналу при использовании четырехуровневых цифровых сигналов? Предполагается, что шума в канале нет.

Using the Nyquist theorem, we can sample 12 million times/sec. Four-level

signals provide 2 bits per sample, for a total data rate of 24 Mbps.

V_max=2Hlog₂V

H – полоса пропускания

V – количество дискретных уровней

5.4 Управляемые носители информации

Назначением физического уровня сети является передача необработанного потока битов от одной машины к другой. Для передачи могут использоваться различные физические носители информации, называемые также средой распространения сигнала. Каждый из них имеет характерный набор полос пропускания, задержек, цен и простоты установки и использования. Носители можно разделить на две группы: управляемые носители, такие как медный провод и оптоволоконный кабель, и неуправляемые, например радиосвязь и передача по лазерному лучу без кабеля. Мы рассмотрим их в следующих разделах.

5.4.1 Магнитные носители

Один из самых простых способов перенести данные с одного компьютера на другой – записать их на магнитную ленту или другой съемный носитель (например, перезаписываемый DVD), физически перенести эти ленты и диски к пункту назначения и там прочитать их. Поскольку такой метод значительно проще применения, скажем, геостационарного спутника связи, он часто оказывается гораздо более эффективным в экономическом отношении, особенно для приложений, в которых высокая пропускная способность или цена за бит являются ключевыми факторами.

Разобраться в данном вопросе нам помогут несложные вычисления. Стандартная кассета с лентой Ultrium вмещает 200 Гбайт. В коробку размером 60x60x60 помещается около 1000 таких кассет, что дает общую емкость 1600 Тбит (1,6 Пбит). Коробка с кассетами может быть доставлена в пределах США в течение 24 часов службой Federal Express или другой компанией. Эффективная полоса пропускания при такой передаче составляет 1600 Тбит/86 400 с, или 19 Гбит/с. Если же пункт назначения находится всего в часе езды, то пропускная способность составит свыше 400 Гбит/с. Ни одна компьютерная сеть пока не в состоянии даже приблизиться к таким показателям.

Если представить себе банк данных на много гигабайт, который должен ежедневно архивировать данные на запасном компьютере (чтобы иметь возможность продолжать работу даже в случае сильного наводнения или землетрясения), то похоже, что никакая технология передачи данных пока и не начала приближаться к производительности магнитных лент.

Если мы теперь взглянем на этот вопрос с экономической точки зрения, то получим сходную картину. Оптовая цена кассеты составляет около $40. Коробка с лентами обойдется в $4000, при этом одну и ту же ленту можно использовать десятки раз. Прибавим $1000 на перевозку (а на самом деле, гораздо меньше) и получим около $5000 за передачу 200 Тбайт или 3 цента за гигабайт. Ни одна сеть на земле не может соперничать с этим. Мораль этой истории такова:

Не думай свысока о скорости передачи данных автомобилем, полным кассет, с грохотом передвигающимся по дороге.

5.4.2 Витая пара

Хотя скорость передачи данных с помощью магнитных лент отличная, однако величина задержки при такой передаче очень велика. Время передачи измеряется минутами или часами, а не миллисекундами. Для многих приложений требуется мгновенная реакция удаленной системы (в подключенном режиме). Одним из первых и до сих пор часто применяемых средств передачи является витая пара. Этот носитель состоит из двух изолированных медных проводов, обычный диаметр которых составляет 1 мм. Провода свиваются один вокруг другого в виде спирали, чемто напоминая молекулу ДНК. Это позволяет уменьшить электромагнитное взаимодействие нескольких расположенных рядом витых пар. (Два параллельных провода образуют простейшую антенну, витая пара – нет.)

Самым распространенным применением витой пары является телефонная линия. Почти все телефоны соединяются с телефонными компаниями при помощи этого носителя. Витая пара может передавать сигнал без ослабления мощности на расстояние, составляющее несколько километров. На более дальних расстояниях требуются повторители. Большое количество витых пар, тянущихся на большое расстояние в одном направлении, объединяются в кабель, на который надевается защитное покрытие. Если бы пары проводов, находящиеся внутри таких кабелей, не были свиты, то сигналы, проходящие по ним, накладывались бы друг на друга. Телефонные кабели диаметром несколько сантиметров можно видеть протянутыми на столбах.

Витые пары могут использоваться для передачи как аналоговых, так и цифровых данных. Полоса пропускания зависит от диаметра и длины провода, но в большинстве случаев на расстоянии до нескольких километров может быть достигнута скорость несколько мегабит в секунду. Благодаря довольно высокой пропускной способности и небольшой цене витые пары широко распространены и, скорее всего, будут популярны и в будущем.

Витые пары применяются в нескольких вариантах, два из которых особенно важны в области компьютерных сетей. Витые пары категории 3 состоят из двух изолированных проводов, свитых друг с другом. Четыре такие пары обычно помещаются вместе в пластиковую оболочку. До 1988 года большинство офисных зданий были оснащены кабелями третьей категории, тянущимися из кабельного центра на каждом этаже в отдельные офисы. Подобная схема позволяла соединять до четырех обычных телефонов или по два многоканальных телефона в каждом офисе с оборудованием телефонной компании, установленном в кабельном центре.

Начиная с 1988 года в офисах стали использоваться более новые витые пары категории 5. Они похожи на витые пары третьей категории, но имеют большее число витков на сантиметр длины проводов. Это позволяет еще сильнее уменьшить наводки между различными каналами и обеспечить улучшенное качество передачи сигнала на большие расстояния. Витые пары категории 5 более приемлемы для высокоскоростной компьютерной связи. Вскоре, вероятно, появятся кабели категорий 6 и 7, способные передавать сигнал с полосой пропускания соответственно 250 и 600 МГц (сравните с полосами в 16 и 100 МГц для категорий 3 и 5).

Все эти типы соединений часто называются UTP (unshielded twisted pair – неэкранированная витая пара), в противоположность громоздким дорогим экранированным кабелям из витых пар корпорации IBM, которые она представила на рынке в 1980 году, но которые так и не стали популярными за пределами фирмы IBM

5.4.3 Коаксиальный кабель

Другим распространенным средством передачи данных является коаксиальный кабель. Он лучше экранирован, чем витая пара, поэтому может обеспечить передачу данных на более дальние расстояния с более высокими скоростями. Широко применяются два типа кабелей. Один из них, 50омный, обычно используется для передачи исключительно цифровых данных. Другой тип кабеля, 75омный, часто применяется для передачи аналоговой информации, а также в кабельном телевидении. В основе такого разделения лежат скорее исторические, нежели технические факторы (например, первые дипольные антенны имели импеданс 300 Ом, и проще всего было использовать уже существующие преобразователи с отношением импеданса 4:1).

Коаксиальный кабель состоит из покрытого изоляцией твердого медного провода, расположенного в центре кабеля. Поверх изоляции натянут цилиндрический проводник, обычно выполненный в виде мелкой медной сетки. Он покрыт наружным защитным слоем изоляции (пластиковой оболочкой).

Конструкция и специальный тип экранирования коаксиального кабеля обеспечивают высокую пропускную способность и отличную помехозащищенность. Максимальная пропускная способность зависит от качества, длины и соотношения сигнал/шум линии. Современные кабели имеют полосу пропускания около 1 ГГц. Коаксиальные кабели широко применялись в телефонных системах, но теперь на линиях большой протяженности их все чаще заменяют оптоволоконными кабелями. Однако коаксиальные кабели все еще широко используются для кабельного телевидения, а также в некоторых региональных сетях.

5.4.4 Волоконная оптика

Быстрое развитие компьютерных технологий вызывает чувство гордости у многих представителей этой индустрии. Первый персональный компьютер фирмы IBM, созданный в 1981 году, работал с тактовой частотой 4,77 МГц. Спустя 20 лет этот показатель вырос до 2 ГГц. Прирост множителя составил 20 за декаду. Не так уж плохо.

За тот же период скорость передачи данных выросла с 56 Кбит/с (ARPANET) до 1 Гбит/с (современная оптическая связь), это означает рост в 125 раз за каждые 10 лет. При этом вероятность ошибки при передаче уменьшилась с 10'5 на бит почти до нуля.

В настоящее время процессоры начинают приближаться к своим физическим пределам. Скорость света преодолеть невозможно, непросто решить и проблему отвода тепловой энергии. Существующая ныне оптоволоконная технология, напротив, может развивать скорость передачи данных вплоть до 50 000 Гбит/с (50 Тбит/с), и при этом много специалистов занято поиском более совершенных материалов. Сегодняшний практический предел в 10 Гбит/с обусловлен нашей неспособностью быстрее преобразовывать электрические сигналы в оптические и обратно, хотя в лабораторных условиях уже достигнута скорость 100 Гбит/с на одинарном волокне.

В гонке компьютеров и средств связи победили последние. Мысль о практически бесконечной полосе пропускания (при ненулевой стоимости, разумеется) еще не усвоена до конца поколением ученыхкомпьютерщиков, приученных мыслить в категориях низких ограничений Найквиста и Шеннона, накладываемых на медный провод. Новая точка зрения должна заключаться в том, что все компьютеры безнадежно медленны, и сетям следует любой ценой избегать вычислений независимо от того, какая часть полосы пропускания при этом будет потеряна. В данном разделе мы рассмотрим технологию передачи данных по оптическому волокну.

Оптоволоконная система передачи данных состоит из трех основных компонентов: источника света, носителя, по которому распространяется световой сигнал, и приемника сигнала, или детектора. Световой импульс принимают за единицу, а отсутствие импульса – за ноль. Свет распространяется в сверхтонком стеклянном волокне. При попадании на него света детектор генерирует электрический импульс. Присоединив к одному концу оптического волокна источник света, а к другому – детектор, мы получим однонаправленную систему передачи данных. Система принимает электрические сигналы и преобразует их в световые импульсы, передающиеся по волокну. На другой стороне происходит обратное преобразование в электрические сигналы.

Такая передающая система была бы бесполезна, если бы свет по дороге рассеивался и терял свою мощность. Однако в данном случае используется один интересный физический закон. Когда луч света переходит из одной среды в другую, например, из стекла (расплавленного и застывшего кварца) в воздух, луч отклоняется (эффект рефракции или преломления) на границе «стекло–воздух». Если угол падения превосходи г некоторую критическую величину, луч света целиком отражается обратно в стекло, а в воздух ничего не проходит. Таким образом, луч света, падающий на границу сред под углом, превышающим критический, оказывается запертым внутри волокна, и может быть передан на большое расстояние почти без потерь.

Только один пойманный луч света, однако поскольку любой луч света с углом падения, превышающим критический, будет отражаться от стенок волокна, то и множество лучей будет одновременно отражаться под различными углами. Про каждый луч говорят, что он обладает некоторой модой, а оптическое волокно, обладающее свойством передавать сразу несколько лучей, называется многомодовым. Однако если уменьшить диаметр волокна до нескольких длин волн света, то волокно начинает действовать подобно волноводу, и свет может двигаться только по прямой линии, без отражений от стенок волокна. Такое волокно называется одномодовым. Оно стоит дороже, но может использоваться при передаче данных на большие расстояния. Сегодняшние одномодовые волоконные линии могут работать со скоростью 50 Гбит/с на расстоянии до 100 км. В лабораториях были достигнуты и более высокие скорости, правда, на меньших дистанциях

5.4.5 Сравнение характеристик оптического волокна и медного провода

Сравнение характеристик оптического волокна и медного провода весьма поучительно. Оптическое волокно обладает рядом преимуществ. Вопервых, оно обеспечивает значительно более высокие скорости передачи, чем медный провод. Уже благодаря этому именно оптическое волокно должно применяться в высококачественных профессиональных сетях. Благодаря низкому коэффициенту ослабления, повторители для оптоволоконной связи требуются лишь через каждые 50 км, по сравнению с 5 км для медных проводов, что существенно снижает затраты для линий дальней связи. Преимуществом оптического волокна также является его толерантность по отношению к внешним электромагнитным возмущениям. Оно не подвержено коррозии, поскольку стекло является химически нейтральным. Это делает оптоволокно идеальным для применения на химических предприятиях.

Это может показаться странным, но телефонные компании любят оптическое волокно еще по одной причине: оно тонкое и легкое. Многие каналы для кабелей заполнены до отказа, так что новый кабель некуда положить. Если вынуть из такого канала все медные кабели и заменить их оптическими, то останется еще много свободного места, а медь можно очень выгодно продать скупщикам цветного металла. Кроме того, оптический кабель значительно легче медного. Тысяча медных витых пар длиной в 1 км весит около 8000 кг. Пара оптоволоконных кабелей весит всего 100 кг при гораздо большей пропускной способности, что значительно снижает затраты на дорогие механические системы. При прокладке новых маршрутов оптоволоконные кабели выигрывают у медных благодаря гораздо более низким затратам на их прокладку.

Наконец, оптоволоконные кабели не теряют свет, и к ним довольно сложно подключиться, что способствует их надежности и сохранности.

Отрицательной стороной оптоволоконной технологии является то, что для работы с ней требуются определенные навыки, которые имеются далеко не у всех инженеров. Кабель довольно хрупкий и ломается в местах сильных изгибов. Кроме того, поскольку оптическая передача данных является строго однонаправленной, для двухсторонней связи требуется либо два кабеля, либо две частотные полосы в одном кабеле. Наконец, оптический интерфейс стоит дороже электрического. Тем не менее очевидно, что будущее цифровой связи на расстояниях более нескольких метров – за волоконной оптикой. Подробнее обо всех аспектах оптоволоконных сетей см. (Hecht, 2001)

5.4.6 Сравнение характеристик оптического волокна и медного провода

5.5 Беспроводная связь

В наше время появляется все большее количество информационных «наркоманов» – людей с потребностью постоянно находиться в подключенном режиме (online). Таким пользователям никакие кабельные соединения, будь то витая пара, коаксиальный кабель или оптическое волокно, не подходят. Им требуются получать данные непосредственно на переносные компьютеры, лэптопы, ноутбуки, электронные записные книжки, карманные компьютеры, палмтопы и компьютеры, встроенные в наручные часы. Короче говоря, они предпочитают пользоваться устройствами, не привязанными к наземным инфраструктурам. Для таких пользователей беспроводная связь является необходимостью. В данном разделе мы познакомимся с основами беспроводной связи, поскольку у нее есть ряд других важных применений, кроме предоставления доступа в Интернет желающим побродить по нему, лежа на пляже.

Существует мнение, что в будущем останется только два типа связи – оптоволоконная и беспроводная. Все стационарные (то есть не переносные) компьютеры, телефоны, факсы и т. д. будут соединяться оптоволоконными кабелями, а все переносные – с помощью беспроводной связи.

При некоторых обстоятельствах беспроводная связь может иметь свои преимущества и для стационарных устройств. Например, если прокладка оптоволоконного кабеля осложнена природными условиями (горы, джунгли, болота и т. д.), то беспроводная связь может оказаться предпочтительнее. Следует отметить, что современная беспроводная связь зародилась на Гавайских островах, где людей разделяли большие пространства Тихого океана и обычная телефонная система оказалась неприменима.

5.6 Электромагнитный спектр

Движение электронов порождает электромагнитные волны, которые могут распространяться в пространстве (даже в вакууме). Это явление было предсказано британским физиком Джеймсом Клерком Максвеллом (James Clerk Maxwell) в 1865 году. Первый эксперимент, при котором их можно было наблюдать, поставил немецкий физик Генрих Герц (Heinrich Hertz) в 1887 году. Число колебаний электромагнитных колебаний в секунду называется частотой, f, и измеряется в герцах (в честь Генриха Герца). Расстояние между двумя последовательными максимумами (или минимумами) называется длиной волны. Эта величина традиционно обозначается греческой буквой λ (лямбда).

Если в электрическую цепь включить антенну подходящего размера, то электромагнитные волны можно с успехом принимать приемником на некотором расстоянии. На этом принципе основаны все беспроводные системы связи.

В вакууме все электромагнитные волны распространяются с одной и той же скоростью, независимо от их частоты. Эта скорость называется скоростью света, с. Ее значение приблизительно равно 3 • 10⁸ м/с, или около одного фута (30 см) за наносекунду. (Можно было бы переопределить, воспользовавшись таким совпадением, фут, постановив, что он равен расстоянию, которое проходит электромагнитная волна в вакууме за 1 не. Это было бы логичнее, чем измерять длины размером сапога какогото давно умершего короля.) В меди или стекле скорость света составляет примерно 2/3 от этой величины, кроме того, слегка зависит от частоты. Скорость света современная наука считает верхним пределом скоростей. Быстрее не может двигаться никакой объект или сигнал.

Величины λ, f, c (в вакууме) связаны фундаментальным соотношением

λ f=c

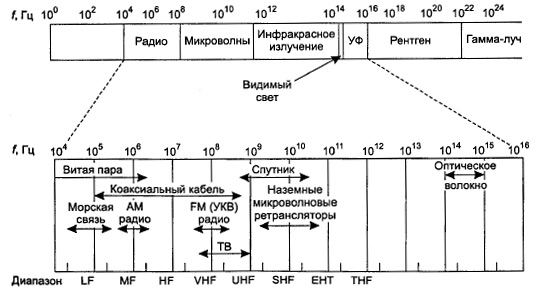
Поскольку с является константой, то, зная f, мы можем определить λ, и наоборот. Существует мнемоническое правило, которое гласит, что 300, если λ измеряется в метрах, f– в мегагерцах. Например, волны с частотой 100 МГц имеют длину волны около 3 м, 1000 МГц соответствует 0,3 м, а длине волны 0,1 м соответствует частота 3000 МГц.

На рис. изображен электромагнитный спектр. Радио, микроволновый, инфракрасный диапазоны, а также видимый свет могут быть использованы для передачи информации с помощью амплитудной, частотной или фазовой модуляции волн. Ультрафиолетовое, рентгеновское и гамма-излучения были бы даже лучше благодаря их высоким частотам, однако их сложно генерировать и модулировать, они плохо проходят сквозь здания и, кроме того, они опасны для всего живого. Диапазоны, перечисленные в нижней части рис., представляют собой официальные названия ITU, основанные на длинах волн. Так, например, низкочастотный диапазон (LF, Low Frequency) охватывает длины волн от 1 км до 10 км (что приблизительно соответствует диапазону частот от 30 кГц до 300 кГц). Сокращения LF, MF и HF обозначают Low Frequency (низкая частота), Medium Frequency (средняя частота) и High Frequency (высокая частота) соответственно. Очевидно, при назначении диапазонам названий никто не предполагал, что будут использоваться частоты выше 10 МГц, поэтому более высокие диапазоны получили названия VHF (very high frequency – очень высокая частота), UHF (ultrahigh frequency – ультравысокая частота, УВЧ), SHF (superhigh frequency – сверхвысокая частота, СВЧ), EHF (Extremely High Frequency – чрезвычайно высокая частота) и THF (Tremendously High Frequency – ужасно высокая частота). Выше последнего диапазона имена пока не придуманы, но если следовать традиции, появятся диапазоны Невероятно (Incredibly), Поразительно (Astonishingly) и Чудовищно (Prodigiously) высоких частот (ITF, ATF и PTF).

Свойства радиоволн зависят от частоты. При работе на низких частотах радиоволны хорошо проходят сквозь препятствия, однако мощность сигнала в воздухе резко падает по мере удаления от передатчика. Соотношение мощности и удаленности от источника выражается примерно так: 1 /г2. На высоких частотах радиоволны вообще имеют тенденцию распространяться исключительно по прямой линии и отражаться от препятствий. Кроме того, они поглощаются, например, дождем. Радиосигналы любых частот подвержены помехам со стороны двигателей с искрящими щетками и другого электрического оборудования.

Благодаря способности радиоволн распространяться на большие расстояния взаимные помехи, вызываемые одновременно работающими пользователями, представляют собой серьезную проблему. Поэтому все государства ведут очень строгий учет владельцев радиопередатчиков, за одним исключением (обсуждаемым далее).

В диапазонах VLF радиоволны LF и MF распространяются вдоль поверхности земли, как показано на рис. 2.10, а. Эти волны можно поймать радиоприемником на расстоянии около 1000 км, если используются низкие частоты, и на несколько меньших расстояниях, если частоты повыше. Радиовещание с амплитудной модуляцией (AM) использует диапазон средних волн (MF), по этой причине, например, передачи Бостонской средневолновой радиостанции не слышны в Нью-Йорке. Радиоволны этих диапазонов легко проникают сквозь здания, вследствие чего переносные радиоприемники работают и в помещениях. Основным препятствием для использования этих диапазонов для передачи данных является их относительно низкая пропускная способность (см. уравнение (23)).

Рис, 2.10. Волны диапазонов VLF, LF и MF огибают неровности поверхности Земли (а); волны диапазона HF отражаются от ионосферы (б)

Радиоволны диапазонов HF и VHF поглощаются землей. Однако те из них, которые доходят до ионосферы, представляющей собой слой заряженных частиц, расположенный на высоте от 100 до 500 км, отражаются ею и посылаются обратно к поверхности Земли, как показано на рис. 2.10, 6. При определенных атмосферных условиях сигнал может отразиться несколько раз. Радиолюбители используют такие диапазоны частот для дальней связи. Военные также осуществляют связь в диапазонах HF и VHF.

ЗАДАЧА:

Радиоантенны обычно лучше всего работают при размере антенны, равном длине волны радиосигнала. Диаметр антенны варьируется в пределах от 1 см до 5 м. Какому диапазону частот это соответствует?

Start with f = c. We know that c is 3 × 10⁸ m/s. For = 1 cm, we get 30 GHz. For = 5 m, we get 60 MHz. Thus, the band covered is 60 MHz to 30 GHz.