Алгоритм нахождения кратчайших путей от заданной вершины х₀

до любой вершины графа (алгоритм Дейкстры)

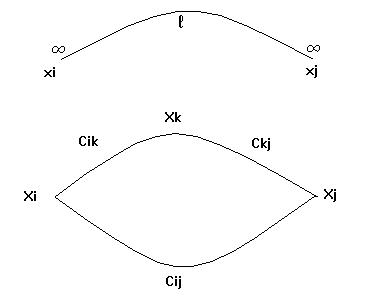
Для решения задачи о кратчайшем пути разработаны различные алгоритмы. Рассмотрим один из них - алгоритм Дейкстры.

1)каждой вершине i ставим в соответствие число l_i  по правилу

x₀->l₀=0,остальным x_i->l_i=D₀ -большое число

2) находим дугу u=(x_i,x_j), для которой l_j-l_i>l(x_i,x_j)

Рисунок 7. Иллюстрация алгоритма

3) заменяем l_j новым значением

l_j->l_j=l_i+l(x_i,x_j), которое будет меньше чем l_j. Заметим, что l_j>0 для всех j<>0.

 Делаем так до тех пор, пока будет  находится дуга, для которой можно уменьшить l_j.

4)    если для каждой u=(x_i,x_j) l_j-l_i<=l(x_i,x_j), то процесс закончен и l_k будут кратчайшими расстояниями от x₀ до x_k.

5)     если нужно найти кратчайшее расстояние между всеми парами вершин графа, то достаточно n-кратного применения алгоритма, выбирая все x_i.

Алгоритм Дейкстры, записанный на ШАЯ, имеет вид

алг кратчайшее( цел N,M,X0,вещ таб X[1:M],Y[1:M],L[1:M],D[1:M])

N-число вершин

M-число дуг

Х0-начальная вершина

X,Y-номера вершин, связывающих дуги

L-длина дуги

D-кратчайшее расстояние

арг N,M,X,Y,L,X0

рез D

начало цел i,j,k,r

k=1;

пока k<=N

нц

D[k]=100000;k=k+1;кц

D[X0]=0;

M1:k=0;r=1;

пока r<=M

нц

i=X[r];j=Y[r];

если D[j]-D[i]>L[r] то

D[j]=D[i]+L[r];k=1 все

r=r+1;

если k>0то k=0;r=1; на M1 все

кц

конец