Динамическое программирование
 

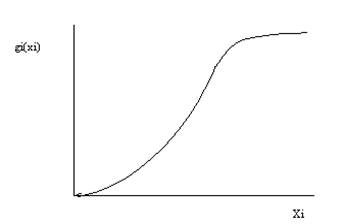
Метод динамического программирования был предложен Беллманом. Решение задач проводится по этапам , с каждым из которых связана только одна управляемая переменная. В основу динамического программирования положен принцип оптимальности, открытый Беллманом, который позволяет получить рекуррентные соотношения, связывающие различные этапы.

Задача формулируется как процесс распределения некоторых ресурсов. Эти ресурсы могут быть употреблены различными способами из-за их ограниченности и столкновения интересов. Каждый способ распределения  называется процессом. В результате употребления всех ресурсов или их части в каком-либо процессе получаем некий доход, который может быть выражен в тех же единицах, что и ресурсы или в других. Размер дохода зависит от количества потребленных ресурсов и от выбранного процесса.

Основные предположения

1) доходы, полученные от разных процессов могут быть оценены общей единицей измерения

2) доход, полученный от любого процесса не зависит от того, какие  количества ресурсов были выделены для других процессов

3) общий доход равен сумме доходов, полученных от отдельных процессов .

Основная задача: распределить ресурсы так, чтобы получить максимальный доход. Пусть имеется N различных процессов, каждому процессу соответствует функция полезности, выражающая зависимость дохода при этом процессе от количества выделенных ресурсов g(xi), где xi-количество ресурсов, выделенных для i-го процесса. Функция полезности имеет следующий вид

Рисунок 15.Функция полезности.

 

1) Небольшое количество выделенных ресурсов не дает доходов

2) Увеличение количества ресурсов приводит к эффекту насыщения.

Независимость процессов и аддитивность доходов позволяет записать общий доход в виде

R(x1,x2,...xN)=g1(x1)+g2(x2)+...gN(xN)    (1)

Задача максимизации возникает по причине ограниченности ресурсов.

   x=x1+x2+x3+...xN, где xi>=0.   (2)

Вместо рассмотрения одной задачи с данным количеством ресурсов и фиксированным числом процессов Беллман предложил рассмотреть целое семейство задач, в которых x может принимать любое больше 0 значение x>0 и N может быть любым целым числом. Сначала какое то количество ресурсов назначается n-му процессу, затем (n-1)-му и т.д. Функция R(x1,...xN)=f(x,N) зависит от x и N. Выделим эту зависимость в явном виде, задав последовательность функций {fN(x)}, определенных для N=1,2,...x>=0 следующим образом

 

fN(x)=max R(x1,x2,..,xN)      (3)

где xi>=0 и Si=1N xi=x.

Функция fN(x) определяет оптимальный доход, получаемый от  распределения x ресурсов по N-процессам. В двух частных случаях  функцию можно записать в явном виде

fN(0)=0 при N=1,2,... (4)

Если gi(0)=0 для любого i, то f1(x)=g1(x) для x>=0.

Найдем рекуррентные соотношения, связывающие fN(x) с fN-1(x) для любых x,N. Пусть xN-количество ресурсов, выделенных для N-го процеса, 0<=xN<=x. Каково бы ни было значение xN, мы знаем, что остающееся количество  ресурсов будет использованы так, чтобы получить максимальный доход от оставшихся (N-1) процессов. Это и есть принцип оптимальности Беллмана: Оптимальное поведение обладает тем свойством, что каковы бы ни были первоначальные состояния и решение в начальный момент, последующие решения должны составлять оптимальное поведение относительно состояния , получающегося в результате первого решения. Так как этот оптимальный доход от распределения количества ресурсов x-xN по N-1 оставшихся процессов по определению есть fN-1(x-xN) , то назначение xN для N-го процесса приводит к  общему доходу. Ясно, что такой выбор xN, который максимизирует эту функцию? Мы получаем основное функциональное уравнение Беллмана

fN(x)=max[gN(xN)+fN-1(x-xN)]

n=2,3,..x>=0,0<=xN<=x. f1(x) определяется по формуле (5).

Основными элементами модели являются:

1) этапы 2) состояние на каждом этапе 3)варианты ,решения на этапе.

Пример:

Судно загружается предметами N-типов, каждый предмет типа i имеет вес Wi и стоимость vi. Грузоподъемность судна- W. Определить максимальную стоимость груза, вес которого не превышает W.

W=5      i  Wi  Vi

N=3      1   2  65

             2   3  80

             3   1  30

Обозначим через ki количество предметов i-го типа. Tогда задача сводится к типу:

   v1k1+v2k2+...+vNkN

w1k1+w2k2++...+wNkN<=W

1) этап j (j=1...N)  ставится в соответствие типу предмета.

2) состояние yj на этапе j выражает суммарный вес предмета.

3) варианты решения kj - описывается количеством предметов типа j.

kj в интервале от 0 до [W/Wj].

Запишем алгоритм для прямой прогонки

f1(x)=max[x1/w1]*v1, где [ ] наибольшее целое <=w

fn(x)=max{knvn+fn-1(x-knwn)}

            kn

где kn пробегает по значениям 0,1,....[x/wn].

Данная задача будет содержать 3 этапа, так как имеется три типа предметов,n=3.

Этап 1

f1(x1)=max[x1/w1]*v1=max{k1v1},w1=2,v1=65,w=5.

k1=0,1,...[x1/w1], x1=0,1,...w

Строим таблицу

x1

k1=0

1

2

f1(x1)

k*1

0

0

-

-

0

0

1

0

-

-

0

0

2

0

65

-

65

1

3

0

65

-

65

1

4

0

65

130

130

2

5

0

65

130

130

2

Для следующих этапов функция рассчитывается по формуле

fn(xn)=max{knvn+fn-1(xn-knvn)}

             kn=0,1,...[xn/wn],xn=0,1,..w

Этап 2

f2(x2)=max{k2v2+f1(x2-k2v2)}, v2=80,w2=3

               k2=0,1,...[x2/w2]   x2=0,1,...w

80*k2+f1(x2-3*k2)

x2

k2=0

1

2

f2(x2)

k2

0

0+0

-

-

0

0

1

0+0

-

-

0

0

2

0+65

-

-

65

0

3

0+65

80+0

-

80

1

4

0+130

80+0

-

130

0

5

0+130

80+65

-

145

1

 

Этап 3

f3(x3)=max{k3v3+f2(x3-k3v3)}

             k3=0,1,...[x3/w3],  x3=0,1,....w    w3=1  v3=30

30*k3+f2(x3-k3)

x3

k3=0

1

2

3

4

5

f3(x3)

k3

0

0

-

-

-

-

-

0

0

1

0+0

30+0

-

-

-

-

30

1

2

0+65

30+0

60+0

-

-

-

65

0

3

0+80

30+65

60+0

90+0

-

-

95

1

4

0+130

30+80

60+65

90+0

120+0

-

130

0

5

0+145

30+130

60+80

90+65

120+0

150+0

160

1

Последняя таблица дает ответ, что оптимальный вариант 1 предмет первого типа и 2 предмета третьего типа.