Элементы теории графов

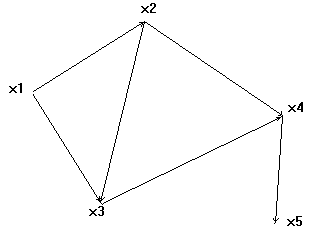
Графом называется пара , состоящая из непустого множества Х  и отображения Г множества х на множество х (Х,Г). Отображением множества Х на множество У называется закон сопоставления каждому элементу х из Х некоторого элемента у из У, т.е. х-->у.

Если одному элементу х сопоставляется несколько элементов у, то отображение называется неоднозначным. В качестве У выступает Х. Элементы множества х обозначаются в виде точек на плоскости, а отображения представляют собой дуги, соединяющие точки. Элементы множества Х преобразуются в виде точек. Поэтому элементы множества Х называют вершинами графа, а пары элементов (х,у) - дугами. Множество дуг можно обозначить U. Тогда граф можно задать так G=(X,U).  Пример графа дан на рисунке 5.

Рисунок 5. Изображение графа

.

Г(х₁)-> {х₂,х₃}  Г(х₂)->{x₄,x₃} Г(x₄)->{x₅} Г(x₃)->{x₄} Г(x₅)->{0}

Можно определить обратное отображение Г^-1 в виде

Г^-1(x₂)={x₁} Г(x₃)={x₁,x₂}

Вершины называются соседними (смежными), если они связаны дугами.

(х₁ и х₃). х₃ и х₅- не смежные.

Путем ориентированного графа называется последовательность дуг, в которой конечная вершина предыдущей дуги является начальной вершиной следующей дуги, за исключением первой и последней дуг.

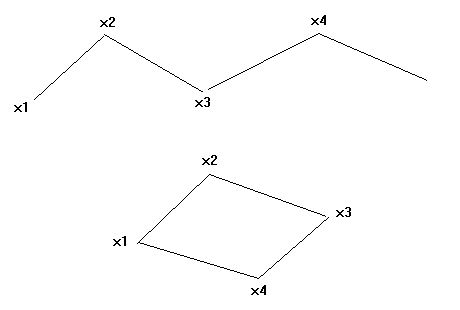
Рисунок 6. Различные варианты графов

Путь называется простым, если ни одна из вершин не встречается дважды. Путь называется элементарным, если ни одна из вершин не встречается дважды. Контуром называется путь, начало и конец которого совпадают.

Если вершинам (или дугам) сопоставлены некоторые числовые характеристики, то граф называется сетью. Пусть длина дуги обозначена l, тогда  длина пути L=S l_i