Геометрический способ решения задачи в случае 2 переменных

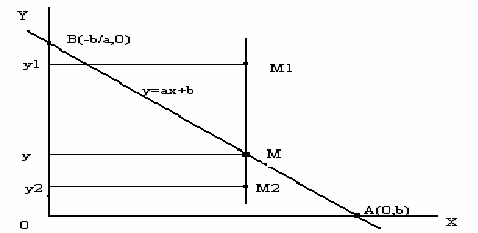
Для линейных уравнений геометрическим образом его является прямая линия на плоскости в случае двух переменных. Ее уравнение можно записать в виде y=ax +b,  где a- тангенс угла наклона прямой, а b- отрезок, отсекаемый на оси y. Прямая делит плоскость на 2 полуплоскости. Рассмотрим какая зависимость между ординатами у1,y,у2, точек М1,м,М2, расположенных над прямой, на прямой и под прямой для одного и того же х. Видно, что для всех точек полуплоскости, расположенной над прямой у1>у, а для всех точек полуплоскости под прямой у2< у, таком образом полуплоскости задаются неравенствами у> ax+b  и y<ax+b.Если считать прямую принадлежащей полуплоскости, то получим неравенства  y>=ax+b и y<=ax+b.

Смотри рисунок 1.

 Рисунок 1. Графическое представление

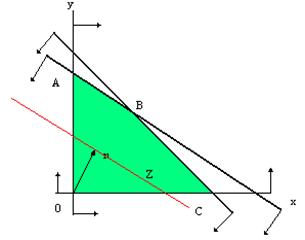
В общем случае уравнение прямой записывается в виде ax+by+c=0. Тогда точки полуплоскостей, получающихся в результате рассечения плоскости прямой описываются неравенствами

                         ax₁+bx₂+c>=0

                         ax₁+bx₂+c<=0,

где обозначение у заменено на х₂, а х на х₁.

Координаты точек, удовлетворяющие заданному неравенству являются решением неравенства. В случае системы из m неравенств из двух неизвестных каждое неравенство определяет некоторую полуплоскость. Так как полуплоскость вместе со своими двумя точками А и В содержит и весь отрезок АВ, то она является выпуклой фигурой. Фигура, состоящая из всех точек, каждая их которых принадлежит всем данным фигурам называется пересечением и в геометрии доказано, что пересечение выпуклых фигур является выпуклой фигурой-многоугольником, который и определяет область допустимых решений системы неравенств. В нашем примере условия неотрицательности ограничивают область первым квадрантом. Другие границы пространства решений изображаются на плоскости прямыми линиями, построенными по уравнениям, которые получаются при замене знаков неравенства на равенство. Области, в которых выполняются соответствующие ограничения в виде неравенств указываются стрелками, направленными в сторону допустимых значений. Геометрическая суть решения сводится к поиску среди множества линий Z=C₁+C₂ такой, которая бы соответствовала бы наибольшему значению Z  и проходила бы через прямоугольник OABC. Чтобы сформулировать правило решения задачи геометрическим способом введем понятие опорной прямой и прямой уровня. Опорной прямой называется прямой, которая имеет с многоугольником решений хотя бы одну общую точку, а все остальные точки многоугольника лежат по одну сторону от нее. Прямой уровня называется прямая, для которой функция Z приобретает одинаковое значение. Вершины многоугольника, через которые проходят опорные прямые, будут искомыми точками. Если задавать Z разные значения, мы получим семейство прямых уровня. Если С₁>0 и C₂>0 то линия уровня С₁x₁+С₂x₂ =0 пройдет через начало координат. Будем перемещать ее параллельно самой себе и следить в какой точке она последней покинет многоугольник. Эта точка ( или линия) и будет оптимальным решением задачи. Смотри рисунок.2.

Рисунок 2. Графический способ нахождения решения

В нашем примере для нахождения значений х₁ и х₂ в точке В нужно решить систему из двух уравнений пересекающихся линий, т.е.

3х₁+4х₂=1700

2х₁+5х₂=1600

Вектор с компонентами dZ/dx₁,dZ/dx₂ (2,4) указывает направление возрастания функции Z, он перпендикулярен линиям уровня и направлен в сторону, противоположную началу координат, так как угловой коэффициент вектора n с координатами (с₁,с₂) к₂=с₂/с₁, а угловой коэффициент функции Z равен к₁=-с₁/с₂ и следовательно линии уровня Z и вектора n перпендикулярны.

Два свойства решения для двумерного случая сохраняются и при переходе к m-мерному случаю:

1)    допустимая область решения всегда является выпуклым многогранником,

2)    оптимальное решение всегда достигается в вершинах или на гранях допустимой области.

Таким образом, можно сформулировать алгоритм геометрического решения

 1.Строим многоугольник решений системы ограничений.

2.Стрoим одну из прямых уровня для произвольного Z  и вектора n(c₁,c₂).

3.Находим опорные прямые, параллельные прямой уровня.

4.Находим координаты х₁,х₂ точек, через которые проходят линии уровня.

5.Находим в этой точке Z.

В общем случае задача линейного программирования состоит в максимизации или минимизации линейной формы  Z=c₁x₁+c₂x₂+...c_nx_n   от n переменных, удовлетворяющих системе  m ограничений

a₁₁x₁+a₁₂x₂+...a_1nx_n<=b₁

a₂₁x₁+a₂₂x₂+...a_2nx_N<=b₂

........................

a_m1x₁+a_m2x₂+...a_mnx_n<=b_m

 и ограничениям положительности

x₁>=0, x₂>=0, .....x_n>=0. В векторном представлении это можно записать в виде

Z=C^TX₀,X₀>=0,A₀X₀<=(=,>=)b.

 Для решения задачу необходимо привести к стандартному виду

1)целевая функция минимизируется

2)все ограничения должны быть записаны в виде равенств с неотрицательными переменными( т.е. все знаки <= заменить на =) и все переменные должны быть >=0.

x₁,x₂,...x_n>=0

 Привести произвольную задачу к стандартному виду можно используя следующие правила:

Для ограничений

1)когда неравенство<=0, то вводится дополнительная переменная

х₁+х₂<=0  ->  х₁+х₂+х₃=0

2)если неравенство >=0, то вводим дополнительную переменную с минусом

х₁+х₂>=0  ->  х₁+х₂-х₃=0

3)для получения неотрицательных переменных обе части неравенства можно умножить

на -1

4)при этом направление знака неравенства меняется на противоположное.

Для переменных

Чтобы х>= 0 было делают замену переменных x_i=x_i'-x_i'', при этом x_i',x_i''>=0.

Подстановка делается во все ограничения и в целевую функцию.

Для целевой функции

1) max F= min(-F)

Пример   z=2x₁+4x₂

         3x₁+4x₂<=1700

         2x₁+5x₂<=1600

Будем минимизировать Z=-2x₁-4x₂ с измененной системой согласно указанных выше правил

3х₁+4х₂+х₃=1700

2х₁+5х₂+х₄=1600

Для решения возникающей системы уравнений можно использовать  симплекс- метод .