Использование теории графов для решения задач линейного программирования

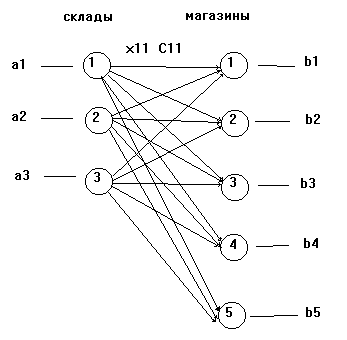
Задачу о транспортных перевозках можно сформулировать графически. Обозначим кружками слева -склады, кружками справа- магазины, соединим их линиями, указывающими направление перевозок и над каждой укажем стоимость и количество перевозимых кроватей. Наличие на складах (объем производства) и спрос укажем входящими и выходящими стрелками. В результате получим рисунок, называемый графом или сетью. Помимо того , что рисунок дает наглядное представление, он позволяет сформулировать и решить задачу с помощью теории графов.

Рисунок 4. Графическое представление задачи

Приведем примеры других задач, которые сводятся к графам и основные типы моделей, возникающих при этом:

    1)проектирование газопровода, соединяющего буровые вышки, находящиеся в заливе со станцией сбора, находящейся на берегу с min стоимостью,

    2)определение кратчайшего пути между двумя городами, проходящего по имеющейся сети шоссейных дорог,

    3)определение max пропускной способности  трубопровода для транспортировки нефтепродуктов,

    4)определение схемы транспортировки нефти из пунктов добычи на перерабатывающие заводы по следующим критериям

        а)по верхнему пределу добычи,

        б)по нижнему пределу для удовлетворения спроса с учетом ограниченной мощности заводов и пропускной способности магистралей.

Оптимизационные задачи на сетях можно описать 4-мя типами моделей:

    1. минимизация сети

    2. нахождение кратчайшего маршрута

    3. определение max потока

    4. минимизация стоимости потока с ограниченными пропускными

способностями коммуникаций.