Алгоритм нахождения max потока методом расстановки меток

Для выполнения алгоритма вводится понятие метка вершины. Каждая вершина может находится в одном из трех состояний:

1)  вершине приписана метка и вершина просмотрена (все смежные вершины просмотрены)

2)  метка приписана, но вершины смежные не просмотрены

3)  вершина не имеет метки

Метки могут быть двух типов

(+x_j,e()),

когда поток допускает увеличение значения вдоль дуги (x_i,y_j), а e- максимальная величина дополнительного потока

(-x_j,e()), когда поток может быть уменьшен вдоль дуги (x_j,x_i).

Шаг 1 (+х₁,d(х_i) d(x_i)=min

[d(x_i),C_ij-f_ij]

2)  x_j принадлежит Г^-1(x_i)       x_i<----àx_j     f_ij>0

Шаг 1 (-x_i,d(x_j)

d(x_j)=min(d(x_i),f_ij)

После совершения шагов вершина х_i будет просмотрена и помечена, а х_j помечены, но не просмотрены.

Шаг 2 повторяем шаг 1 до тех пор, пока не достигнем стока. Либо получится ситуация, когда вершину стока пометить не удается, а других пометок поставить нельзя. В этом случае достигнут max поток в сети.

Шаг 3 (увеличение потока)

полагаем х=t.

Шаг 4 Если вершина Х имеет пометку вида (+z,dх)), то изменяем поток вдоль дуги(z,x) таким значением f(z,x)àf(z,x)+d(t)

Если пометка имеет вид (-z,d(х)), то заменяем поток вдоль дуги (z,x)

f(z/x)->f(z,x)-d(t).

Шаг 5 Если z=s то стираем все пометки и возвращаемся на шаг 1. Но вдоль дуг уже будут другие потоки. Если z<> s, то x=z  и возвращаемся на шаг 4

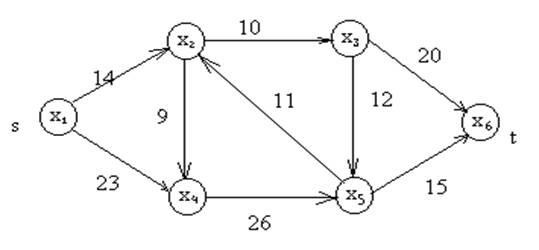
Рисунок 17. Пример задачи

Цифры на графике -максимальные пропускные способности. Необходимо найти мах поток.

1)(+х₁,¥)-вершина

{x_j|x_jÎГ(х₁) и f_ij<C_ij}=x₂,x₄

f_ij=0

Для вершины х₂ пометка следующая:

(+x₁,min(¥,14-0)), т.е. (+х₁,14)

Для х₄ пометка будет (+х₁,23)

Пример обозначения потоковых задач

Введено понятие внешних потоков.

В (    ) задается характеристика дуги, а в [   ]-характеристика узла. Например

(С_к,f_к,h_к,а_к)

к-номер дуги

f_к- реальный поток по дуге

h_к- стоимость передачи единицы потока по дуге

а_к- min поток по дуге

С_к -max поток по дуге

[b_i, b_si, h_si]

b_i- фиксированный внешний поток в узел

b_si- свободный внешний поток в узел

h_si- цена единицы передачи внешнего потока.

 Внешние потоки отражают связь изучаемой системы с внешним миром. Фиксированные внешние потоки во время решения задачи не изменяются, а свободные потоки изменяются. В этом случае выполняется закон сохранения потока: Сумма потоков  втекающих в узел по дугам и внешних потоков равна сумме потоков вытекающих из узла.

Управляемой переменной здесь является потоки. Ограничения накладываются структурой графа, фиксированными внешними потоками, максимальными пропускными способностями.

Свободные потоки можно представить иначе, используя параметры дуг. При этом у узлов будет меньше параметров и они будут переносится на дуги. Для этого вводится свободный узел, в котором не требуется выполнения сохранения потока. Для положительного свободного потока f_si вводится дуга, а для отрицательного свободного потока вводится обратная дуга. Если характеризовать пропускную способность b_si, стоимость-h_si, тогда характеристики графа будут [b_i] и (С_к,h_к).

Все задачи сводятся к задаче минимизации стоимость передачи потока.