Метод решения целочисленных задач.

Особенности решения целочисленных задач

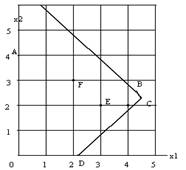
Пример: пусть x₁,x₂-целые и имеем следующую задачу

x₁>=0,x₂>=0-ограничения, наложенные на задачу

2x₁+11x₂<=38

x₁+x₂<=7

4x₁-5x₂<=5

Найти Z=x₁+x₂-max

Рисунок 3. Иллюстрация поиска решения

Выкинем условия целочисленности и решим задачу как обыкновенную. Получим решение В(4 1/3,2 2/3), С(4 4/9,2 5/9), при отбрасывании дробной части получаем решение В(4,2),С(4,2)- лежащее вне области допустимых решений. Настоящее решение E(3,2),F(2,3) лежит в  области допустимых решений. Таким образом стандартные методы не подходят для решения таких задачи. Для решения целочисленных задач разработано три метода:

-метод отсечений Гомори,

на задачу накладываются дополнительные ограничения, которые отсекают нецелочисленные области

-метод ветвей и границ ( комбинаторный метод)- основан на идее перебора всех целочисленных решений

-эвристический метод (случайного поиска) -использует метод Монте-Карло.

Рассмотрим подробно метод Гомори. Сначала к задаче применяется симплекс-метод, игнорируя условие целочисленности. При этом получаются некоторые нецелочисленные решения.

     x₁₁  x₁₂ ....x_1n    a_j<=0,b_i-нецелое

x_k1  a₁₁  a₁₂     a_{1n b1}-оптимальное решение, которое может

x_k2  a₂₁  a₂₂     a_2n b₂ быть нецелочисленным

.......

x_kn  a_m1  a_m2 ... a_mn b_m

Введем и построим дополнительные ограничения по правилу

l_ij=a_ij-[a_ij]=a_ij-t_ij-целая величина,[ ]-целая часть.

t_ij<a_ij<t_ij+1

 ei=b_i-[b_i]=b_i-t_i,где

t_i<b_i<t_i+1

Определим

S_i=l_i1x_l1+l_i2x_l2+...+l_inx_ln-e_i>=0

S_i=S_j=1ⁿ l_ij*x_lj-e_i>=0

Покажем, что при целых значениях x_lj,x_ki величина S_i будет целой

S_i=S_j=1ⁿ (a_ij-t_ij)*x_ij-b_i+t_i

x_ki+S_j=1ⁿ a_ijx_lj=b_i==>S_j=1ⁿ a_ijx_lj-b_i=-x_kj

S_i=-S_j=1ⁿ t_ijx_lj-x_ki+t_i

              -------------- - целая часть, а значит и S_i-целое

и S_i=-e_i, а  e_i<=0.

Этот метод не гарантирует оптимального решения.