Расчет параметров сетевых график

Расчет параметров сетевых графиков

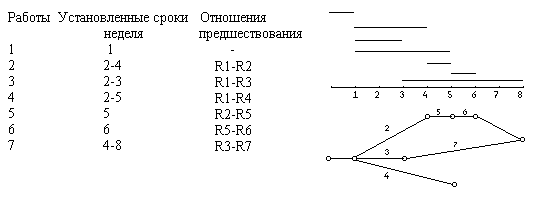
Важнейшим этапом сетевого планирования является анализ по критериям времени. С этой целью рассчитываются ранние и поздние сроки начала и окончания работ, полный резерв времени, критический путь. Для нахождения сроков раннего начала и позднего окончания каждой работы достаточно рассчитать ранние и поздние сроки наступления событий в сетевом графике. Событие совершается в тот момент, когда все предшествующие ей работы полностью выполнены, поэтому время раннего начала совпадает с ранним свершением события непосредственно предшествующего данной работе. Так как существует несколько путей из начального события, то время раннего наступления события характеризуется продолжительностью максимального пути, идущего из начального события. Время раннего наступления событий рассчитывается слева направо, начиная с начала.

T₁рнс=0

Сроки раннего свершения остальных событий определяются по формуле

t_j рнc=max(t_iрнс+t_ij)

t_iрнс- время раннего свершения i- го события, непосредственно предшествующего j- му событию, t_ij- продолжительность работы.

Время раннего свершения конечного события равно продолжительности max пути, идущего из начального события в конечное и этот путь называется критическим. Критическими называются и все события и работы , которые лежат на этом пути. Время раннего свершения конечного события определяет минимальный срок выполнения всего комплекса работ. Время позднего наступления события (пнс) рассчитывается в графике, начиная с конца?.

Сроки позднего свершения остальных событий вычисляются по формуле

t_i пнс= min( t_jпнс-t_ij)

Знание ранних и поздних свершения событий может определять ранние и поздние сроки начала и окончания работ, полный резерв времени для каждой работы и критический путь. Для каждой работы (i,j) определяются следующие параметры:

ранний срок начала работы:t_ijрн=t_iрнс

ранний срок окончания работы: t_ijро=t_ijрн+t_ij

поздний срок окончания работы: t_ij по=t_ij пнс

поздний срок начала работы: t_ijпн=t_ij по-t_ij

полный резерв времени работы:R_ij=t_ijпо-t_ijрн-t_ij равен разнице

Полный резерв времени работы показывает на сколько можно отодвинуть сроки начала работы или увеличить ее продолжительность, не нарушая минимального срока выполнения всего комплекса работ.

Пример. Для графика критический путь будет состоять из работ (1,2), (2,3),(3,4),(4,6) и min срок выполнения работ =15. Критические работы резерва времени не имеют, поэтому чтобы не сорвать срок выполнения всего комплекса работ основное внимание уделяют выполнению критических работ, обеспечивая их материальными ресурсами.

10 'расчет параметров сетевого графика

20 dim x(300),y(300),t(300),l1(200),l2(200)

30 input"Введите два числа:кол-во событий сетевого

графика<200 и кол-во работ<300";n,m

50 for r=1 to m

60 read x(r),y(r),t(r)

70 next

80 l1(1)=0:l2(n)=0

90 for j=2 to n

100 l1(j)=-100000:l2(j-1)=-100000

110 next j

120 k=0

130 for j=1 to m

140 i=r(r):j=y(r)

150 if l1(j)-l1(i)>=t(r) then 170

160 l1(j)=l1(i)+t(r):k=1'вычисление времени раннего наступления

события

170 next

180 if k>0 then 120

190 k=0

200 for r=1 to m

210 i=y(r):j=x(r)

220 if l2(j)-l2(i)>=t(r) then 240

230 l2(j)=l2(i)+t(r):k=1

240 next r

250 if k>0 then 190

260 for i=2 to n

270 l2(i)=l1(n)-l2(i)'вычисление времени позднего наступления

события

280 next i

290 print"параметры сетевого графика": print

300 print"шифр продол-сть РН РО ПН ПО полный резерв"

310 for r=1 to m

320 i=y(r):j=y(r)

330 b=l2(j)-t(r)'вычисление времени позднего начала (ПН) работы

340 s=l1(i)+t(r)'вычисление времени раннего окончания (РО) работы

350 p=l2(j)-l1(i)-t(r)'расчет полного резерва времени

360 print x(r);y(r);t(r);l1(r);c,b,l2(j);p

370 next r:print

380 print"min срок окончания всего комплекса работ Д=";l1(n)

390 'исходные данные(начало,конец,продолжительность)

400 data 1,2,5,1,3,2,2,1,4,4,2,5,1,3,5,6,3,4,4,4,6,5,5,6,2

410 end

Сетевые графики могут быть объединены с графиками Ганта

Рисунок 14. Объединение сетевых графиков с диаграммами Ганта

Особенности составления расписаний рассмотрим на примере: 5 девушек пошли в парикмахерскую делать прически. Длина волос у них разная, поэтому на обслуживание каждой тратится разное время в таблице1

Вид операции Оля1 Галя2 Наташа3 Лена4 Миля5

укладка 1 15 20 10 13 25

сушка 2 20 10 5 30 20

Общая длительность обслуживания будет зависеть от порядка обслуживания.

Например, обслужим их в порядке 31254.

Таблица

N Очередь имя Укладка Сушка

начало конец начало конец

3 Наташа 0 10 10 15

1 Оля 10 25 25 45

2 Галя 25 45 45 55

5 Миля 55 70 70 90

4 Лена 70 83 90 120

Все подружки будут сидеть 2 часа.

Нарисуем график Ганта для этого случая

Время 0 10 25 45

31 11 21

Укладка [-------[-----------[----------------[

32 12

Сушка [---]прост[----------------[

32- 3-я девушка,2-я операция

Если решать задачу простым перебором, то придется просмотреть 5*4*3*2*1=5!=120 вариантов. Поручим это дело машине. Введем массивы

О[1:5] - очередь

А[1:5]- 1 строка табл 1-->время затраченное на укладку

Б[1:5]- 2 строка табл 1 ->время затраченное на сушку

У[1:2,0:5] - половинка табл 2 - укладка

С[1:2,0:5] - вторая половинка табл 2 - сушка

Например, у[1,3]-время начала укладки у Наташи,1-начало,2 -конец.

P=1,2,3,4,5 номер девушки

i=номер девушки в очереди

Тогда О(i)=P

Расчет времени ведется по следующим формулам

Y(1,i)=Y(2,i-1)

Y(2,i)=Y(1,i)+A(P)

Y(1,0) Y(2,0) C(1,0) C(2,0)-

C(1,i)=max( Y(2,i),C(1,i-1))

C(2,i)=C(1,i)+B(P)

Алгоритм время обслуживания (цел таб О[1:5],вещтаб А[1:5],B[1:5],

вещ Т)

арг О,А,В

рез Т

начало цел i,r,вещтаб Y[1:2,0:5],C[1:2,0:5]

i=1;Y(1,0)=0;y(2,0)=0;C(1,0)=0;C(2,0)=0;

пока i<=5

нц

P=O(i);Y(1,i)=y(2,i-1);Y(2,i)=Y(1,i)+A(P)

если Y(2,i)>=C(1,i-1) то

C(1,i)=y(2,i) иначе C(1,i)=C(1,i-1) все--определение max

C(2,i)=C(1,i-1)+B(P);

i=i+1;

кц

T=C(2,5)

конец