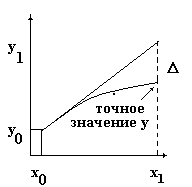2.1.2. Алгоритм Эйлера

     Типичный метод численного решения дифференциального уравнения включает в себя преобразование его в конечно-разностное уравнение. Проанализируем уравнение (2). Положим, что при х=х₀ функция у принимает значение у₀. Поскольку уравнение (2) описывает изменение функции у в точке х₀, то можно найти приближенное значение функции у в близлежащей точке х₁=х₀+Dx, если приращение аргумента Dх мало. В первом приближении предполагается, что функция g(x) (или скорость изменения у) постоянна на отрезке от х₀ до х₁. В этом случае приближенное значение функции в точке х₁=х₀+Dх определяется выражением

Данный метод называется методом касательных или методом Эйлера. Геометрическая интерпретация метода Эйлера имеет следующий вид.

Рис. 1. График точного и приближенного решения

Предположение, что g(x) постоянна на отрезке от x_n до x _n-1, означает, что скорость изменения функции у на отрезке от x _n-1 до x _n постоянна и наклон касательной вычисляется в начальной точке x _n-1 отрезка. В случае, если наклон касательной меняется на некотором отрезке, появляется отклонение от точного решения D. Его можно уменьшить, уменьшая dx. Приближению Эйлера и истинной функции соответствует прямая и кривая рисунка. Запишем алгоритм решения задачи для следующих начальных условий Т₀=83,Т_s=22, R=0.1, t_max=2, Dt=0.1. В этом случае общее число шагов (точек) n=t_max/Dt=200. Тогда программа может иметь следующий вид

10 T=0:DT=0.1:R=0.1:N=2/DT:T1=83:TS=22

1.     Пусть начальная разность температур Т₀-Т_s = 61. Сколько  времени нужно, чтобы разность стала равной 61/2, 61/4, 61/8?

2.     Аналитическое решение уравнения (1) имеет вид

T(t)=T_s-(T_s-T₀)exp(-rt),

где T(t=0)=T_s-(T_s-T₀)=T₀,а  T(t®¥)=T_s.

Вычислите Т в момент t=1  с шагом Dt = 0.05, 0.025, 0.014, 0.005. Выберите реальное r.

Постройте таблицу, содержащую разность между точными и численными решениями уравнения как функцию от Dt. Будет ли эта разность убывающей функцией от Dt? Если шаг уменьшить в два раза, как изменится разность? Нарисуйте график разности как функцию от Dt. Если точки приблизительно расположены на убывающей прямой, разность пропорциональна Dt (при Dt<<1). Если она пропорциональна (Dtⁿ) – то численный метод называется методом n-го порядка. Какой порядок точности у метода Эйлера?

3.     Какой нужно выбрать шаг Dt, чтобы достигнуть точности  0.1% в момент t = 1? Какой должен быть Dt, чтобы точность 0.1% была в точке t = 5?

4.     Уравнение RdQ/dt=V-Q/C описывает заряд конденсатора в RC цепи с напряжением V, t меряется в сек, R = 2000 Ом, C = 10^-6Ф и V = 10 В. Начальное условие Q = 0 при t = 0. Будет ли расти Q (t) со временем, увеличивается ли Q до ¥ или будет насыщение? Напишите программу численного решения методом Эйлера. Какой надо взять шаг Dt, чтобы получить три правильных знака в момент t = 0.005 с. Каковы особенности численного решения при Dt = 0.005, 0.004 и 0.003? Приводит ли малое изменение шага Dt к большому изменению Q? Устойчив ли метод для любого шага?