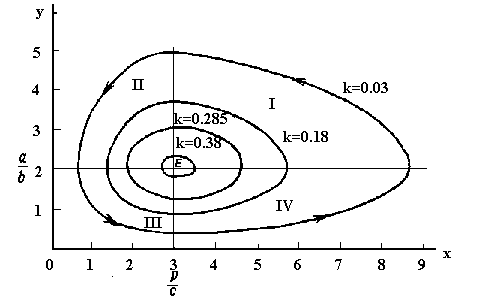
2.2.2. Борьба популяций в теоретической экологии

Рассмотрим взаимодействие двух видов животных, один из которых служит пищей для другого [5]. Пусть животные первого вида- кролики, второго- лисы. Аналогичной задачей является распространение эпидемий с помощью бактерий, здесь можно рассматривать население как животные первого вида, а бактерии- второго вида.

Рассмотрим животных первого вида. Если нет лис, то популяция кроликов будет увеличиваться (другие факторы, влияющие на рост этих видов животных, остаются неизменными, как переменная величина учитывается только число животных). Простейшим предположением является, что скорость роста популяции кроликов пропорциональна размеру популяции. Пусть х - число кроликов, у- число лис в момент времени t. Тогда, если у=0, то dx/dt=ax, a>0 (5).

С другой стороны, не имея пищи, лисы будут вымирать, так что получаем, если х=0, то dy/dt=-py, p>0. (6) Если же имеются и кролики и лисы, то необходимо принять во внимание их взаимодействие. Предположим, что число съеденных кроликов пропорционально величине xy. Тогда необходимо добавить в (6) член, пропорциональный ху, чтобы позволить увеличение числа лис при наличии пищи и вычесть такой же член из (5), чтобы учесть съедаемых кроликов

dx/dt=ax-bxy a, b>0

dy/dt=cxy-py c, p>0. (7)

Мы получили динамическую модель взаимодействия двух видов животных, она описывается системой дифференциальных уравнений первого порядка.

Для решения такой системы могут применяться различные методы. Общий вид полученной системы уравнений можно записать так

dx/dt=F(x, y)

dy/dt=G(x, y) (8)

Подсчитаем количество животных каждого вида в данный момент времени, который можно принять за t=0, и получим x=x₀>0 кроликов и y=y₀>0 лис. Нашей главной задачей является определение численности обеих популяций в будущем. При делении уравнений друг на друга время исключается и получаем уравнение вида

dy/dx=G(x, y)/F(x, y) (9)

Для таких систем уравнений доказаны две теоремы.

Теорема 1: Если в окрестности точки плоскости (х₀,у₀) частные производные функций F и G непрерывны, то существует единственное решение, проходящее через (х₀, у₀) при t=0. Решения либо не зависят от времени, либо описываются гладкой кривой. Кроме того, решение x(t) и y(t) непрерывно зависят от начального положения. Существуют три типа решений: устойчивые, неустойчивые и циклические.

Теорема 2: Поведение траектории вблизи точки равновесия можно определить, рассматривая только линейные члены разложения функций F и G в ряды Тейлора в точке равновесия (которая случается при F=G=0). Решения получаемых линейных уравнений в окрестности точки равновесия имеют то же поведение, что и точные решения.

Все сказанное справедливо и для n уравнений с n неизвестными

dx_i/dt=F_i(x₁, x₂,…x_n), i=1..n (10)

Интересной точкой равновесия является точка E=(p/c, a/b). Исследуем поведение вблизи E. Положим

u=x-p/c и v=y-a/b

Тогда du/dt=dx/dt=-(u+p/c)bv и dv/dt=dy/dt=cu(v+a/b)

Линейные части этих уравнений есть

du/dt=-(bp/c)v, dv/dt=(ac/b)u (11)

Рассмотрим эти уравнения как точные (согласно теореме 2). Дифференцируем первое уравнение и, подставляя dv/dt из второго, получим

d²u/dt²=-apu (12)

Следовательно, движение будет периодическим. Поскольку значение начального момента неважно, начнем с момента, когда u=0. Решение (12) тогда есть u=Asin(Öap t) и из (7) получим v=Bcos(Öap t).Следовательно, u²/A²+v²/B²=1, т.е. траектория есть эллипс (рис. 3).

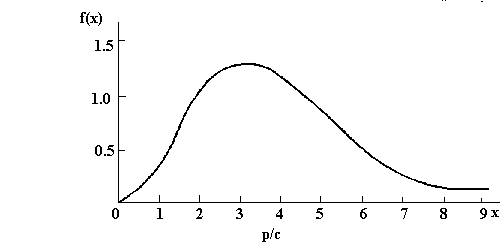
Рис. 3. Траектории x^py^a/e^cxe^bx=k при а=4, b=2, c=1, p=3

Таким образом, вблизи точки равновесия Е траектории суть периодические движения вокруг точки равновесия. В первом приближении эти траектории являются эллипсами с периодом обращения 2p/Öap.

Для нахождения точных траекторий образуем уравнение согласно (9)

dy/dx=y(cx-p)/x(a-by) (13).

Отсюда

(a-by)/y dy/dx+(p-cx)/x=0.

Интегрируя по х, получаем a lg y-by+p lg x-cx=lg k или

x^p/e^cxy^a/e^by=k (14)

Так как k не зависит от времени, то k=x₀^py₀^a/e^cxoe^by⁰.

Следовательно, мы нашли уравнения для траектории, соответствующей данному начальному положению. Функция x^p/e^cx и y^a/e^by могут быть выражены графически (рис. 4).

Всякое значение за исключением экстремального она принимает 2 раза. Следовательно, если в (14) зафиксировать х, то ему соответствуют два значения у и наоборот. Максимальное и минимальное значение принимаются переменной у при x=p/c и переменной x при y=a/b. Причем не существует точки перегиба. Из выражения (7) следует, что dx/dt>0, если и только если y<a/b. Следовательно, в нижней части траектории x увеличивается, а на верхней части уменьшается, таким образом, движение идет против часовой стрелки. Вычислим средние значения х и у.

Поскольку движение циклическое, можно взять среднее по одному циклу.

Рис. 4. f(x)=x^p/e^cx при c=1, p=3

Пусть T- длина цикла. Из (7) имеем 1/x dx/dt=a-by.

ò_o^T1/x dx/dt=ò₀^T(a-by)dt; lg(x(T))-lg(x(0))=aT-bò₀^Tydt=T[a-by] (15)

Но (0, T) есть полный цикл, следовательно, y=a/b. Аналогично x=p/c. Эти средние не зависят от начального положения и совпадают с координатами точки равновесия E.

Для явного получения траектории движения используем Mathcad для того, чтобы прямо решить систему уравнений (7) при следующих начальных условиях a=4, b=2, c=1, p=3.

Задачи для самостоятельной работы

1. Рассмотрим модель двух хищников, каждый из которых имеет свою скорость увеличения a и p. Численность обоих уменьшается пропорционально xy. И их численность описывается системой уравнений

dx/dt=ax-bxy a, b>0

dy/dt=py-cxy p, c>0 (16)

Для этой модели получаем

du/dt=-(bp/c)v, dv/dt=-(ac/b)u и d²u/dt²=apu. (17)

Решение не является периодическим и есть u=Ae^st+Be^-st, где s=Öap. Дифференцируя это и подставив в (16), получим v=-rAe^st+rBe^-st, где r=cs/bp. Из этих формул получаем u²-(v/2)²=4AB. Следовательно, траекториями первого приближения являются гиперболы с центром в E. Используйте Mathcad для получения вида этих траекторий с теми же самыми начальными условиями.

1. На рынке товаров имеется два производителя товаров, один производит х товаров, второй - у товаров. Они обмениваются друг с другом товарами, первый отдает второму долю q (0<q<1) в обмен на такую же долю товаров другого. У каждого остается по p=1-q своего товара и доля q- чужого. Изменение товаров описывается системой уравнений

dx/dt=p/(px+qy+1)-p/2

dy/dt=p/(qx+py+1)+p/2 (18)

Покажите, что, либо производство приближается к равновесию, либо один из производителей покидает рынок. Кто покидает рынок - зависит от начальной продукции обоих производителей.

2. Рассмотрим модель популяций системы паразит –хозяин. Развитие нападающего вида зависит от доступного ему числа пищи. Если принять, что рождаемость хозяев зависит от числа хозяев N_t и что смертность хозяев пропорциональна числу паразитов P_t, то скорость изменения популяций определяется уравнениями

dN_t/dt=(r_n-c₁P_t)N_t

dP_t/dt=(-r_p+c₂N_t)P_t(19)

r_n- собственная скорость увеличения популяции хозяина, которая снижается для данного t в зависимости от численности паразитов P_tлинейно. В отсутствии хозяев паразиты гибнут со скоростью r_p. Последняя компенсируется фактором размножения c₂ при общем числе хозяев N_t. Разделив уравнения друг на друга, получим

dN_t/dP_t=(r_n-c₁P_t)N_t/(-r_p+c₂N_t)P_t_.

Отсюда получаем

R_plnN_t-c₂N_t+r_nlnP_t-c₁P_t=const (20).

Равенство соответствует набору замкнутых кривых. Достижение равновесия происходит, когда

dN_t/dt=dP_t/dt=0 и соответствует значениям N=r_p/c₂ и P=r_n/c₁. Учтем конкуренцию хозяев, изменив уравнение следующим образом

dN_t/dt=(r_n-c₁P_t-bN_t)N_t

Получите решение с помощью Mathcad график зависимости P_t от N_t.