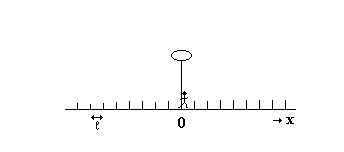
4.1. Одномерная модель случайных блужданийПьяница может двигаться от фонарного столба только по прямой направо либо налево (рис. 5) . Все шаги одинаковы по длине и равны l. Направление движения не зависит от предыдущих шагов. Пьяница делает шаг вправо с вероятностью р и шаг влево с вероятностью q=1-p. Пусть n1- число шагов вправо, а n2- число шагов влево. Полное число шагов N=n1+n2.
Рис. 5. Одномерные случайные блуждания пьяницы Тогда полное смещение от фонарного столба (координата 0) после N шагов равно x=(n1-n2)*l, где –Nl<=x<=Nl. Определим вероятность того, что после N шагов пешеход окажется на расстоянии x от столба. Среднее смещение <xN> и дисперсия <Dx2N> даются формулами <xN>= SNl x=-Nl xPN(x) и<Dx2N>=<x2N>-<xN>2, (27) где <x2N>= SNlx=-Nl x2 PN(x) и PN(x) есть вероятность того, что после N шагов пешеход окажется на расстоянии x от столба. Усреднение проводится по всем блужданиям из N шагов. Задача имеет аналитическое решение, полученное по марковской теории цепей, вида <xN>=(p-q)Nl и < x2N>=4pqNl2. (28) В симметричном случае p=q=1/2 значение <xN>=0. Программа, реализующая случайное блуждание приведена ниже 5 CLS 10 SCREEN 920 LINE(0,175)-(640,175) 30 CIRCLE(320,150),540 LINE (320,155)-(320,170) 50 FOR I=0 TO 640 STEP 10 60 LINE(I,172)-(I,177) 70 NEXT 75 FOR D=1 TO 100 77 X=0 80 FOR I=1 TO 100 90 A=RND(1) 100 IF A>0.5 THEN X=X+10 ELSE X=X-10 110CIRCLE(320+X,175),2,I MOD 15 115 FOR I=0 TO 30000: NEXT 120 NEXT 130 PRINT X 140 NEXT Задание на самостоятельную работу Сравните точное и имитационное решение, совпадают ли они? |