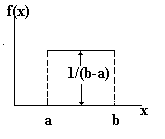|
6.1 Равномерное распределение Функция плотности вероятностей равномерного распределения на промежутке [a, b] имеет вид f(x)= 1/(b-a) для a<x<b и 0 иначе(39) График равномерного распределения изображен на рис. 16.
Здесь х - случайная величина, определенная на интервале [a, b]. Это самое простое непрерывное распределение с функцией плотности вероятностей постоянной на интервале [a, b] и равной нулю вне его. Оно часто применяется в имитационных методах, так как простое и используется для получения других распределений. Кумулятивная функция распределения F(x) равномерно распределенной случайной величины X есть F(x)=òax1/(b-a)dx=(x-a)/(b-a), 0 £ F(x)<1. (40) Для имитации равномерного распределения на интервале [a, b] сначала генерируются случайные числа r, равномерно распределенные в [0, 1], затем вычисляют х по формуле x=a+(b-a)*r, 0 £ r £ 1. (41) Каждое случайное число однозначно определяет реализацию равномерно распределенной случайной величины Х. Программа генерирования равномерного распределения, заданного на интервале [a, b], имеет вид
10 INPUT A,B 20 FOR I=1 TO 100 30 R=RND(1) 40 X=A+(B-A)*R 50 PRINT X 60 NEXT Методы генерирования других вероятностных распределений основаны на обратном преобразовании и на использовании центральной предельной теоремы.
|