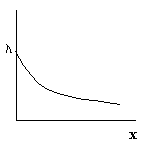6.2. Экспоненциальное распределение

     Когда вероятность наступления события в малом интервале времени Dt очень мала и не зависит от наступления других событий, то интервалы времени между последовательными событиями распределены по экспоненциальному закону (рис. 17). Оно имеет плотность вероятности

f(x)=le^-ax с математическим ожиданием m=1/l и дисперсией s=1/l² .

Рис. 17. Экспоненциальное распределение

Если в какой-либо ситуации с очередями появление клиентов имеет пуассоновское распределение с параметром l, то интервалы времени между их появлениями имеют экспоненциальное распределение с параметром 1/l. Этому закону распределения подчиняются многие явления, например, длительность телефонных переговоров, срок службы многих электронных деталей, время поступления заказов на предприятие, время прибытия самолета в аэродром и т.д. Для генерирования случайных чисел, распределенных по экспоненциальному закону, используем обратное преобразование. Если случайная величина h имеет плотность распределения f_h(x), то распределение случайной величины x

x=ò_-¥^hf_h(x)dx (42)

является равномерным в [0, 1]. Следовательно нам нужно найти функциональную зависимость исходной случайной величины h и равномерно распределенной в [0, 1] величины x , т.е. h=j(x). Если уравнение (42) разрешить относительно h, то найдем j. Если f_h(x)=le^-lx ,то xi=ò₀^hi le^-lx dx и интегрируя , получаем h_i=-1/l*ln(1-x_i).Поскольку распределение величины x_i  имеет тот же вид, что и распределение (1-x_i), то последнее выражение можно записать в виде 

h_i=-1/l*lnx_i (43)

и оно может быть использовано для генерации случайной величины h_i. Тогда длина интервала между (i-1)-ым и i-м событиями задается формулой (43), а моменты поступления заявок в потоке определяются согласно формуле

t₁=t₀+h₁,t₂=t₁+h₂,..., t_k=t_k-1+h_k. (44)

Программа, генерирующая такие величины, имеет вид

10 INPUT “Введите параметр l“; L

20 A=RND(1)

30 X=-LN(A)/L