|
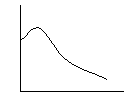
6.3. Пуассоновское распределение Распределением Пуассона можно описать целый ряд реальных процессов. Если взять серию из n независимых испытаний по схеме Бернулли ( да- нет, успех- неудача и т. п.) с малой вероятностью появления событий в каждом из них, то с ростом n вероятность того, что мы будем наблюдать появление событий х раз, подчиняется пуассоновскому закону распределения ( рис. 18)
Рис. 18. Распределение Пуассона
Распределение Пуассона имеет плотность вероятности f(x)=lxe-l/x! с математическим ожиданием m=l и дисперсией s=l. Этим распределением, например, описываются многие явления на определенном отрезке времени, например, количество пожаров, авиакатастроф, ураганов, крушений морских судов и т. д. Распределение Пуассона относится к числу дискретных (т.е. таких, при которых переменная может принимать лишь целочисленные значения, включая нуль) с математическим ожиданием и дисперсией, равными l. В теории вероятностей показано, что если моменты появления событий на некотором временном интервале имеют экспоненциальное распределение, то число появлений событий, приходящееся на каждый интервал, будет распределено по закону Пуассона. Отсюда следует метод вычисления значений переменных, подчиняющихся закону Пуассона - генерируются экспоненциально распределенные моменты наступления событий с математическим ожиданием 1, которые потом суммируются до тех пор, пока итог не превысит величину l. Т.е., производится генерирование случайных значений переменной ri, равномерно распределенных в интервале от 0 до 1, до тех пор, пока не станет справедливым соотношение Pi=0 x ri ³ e-l > Pi=0 x+1 ri. (45) Этот метод реализуется следующей программой 10 INPUT “Введите l“; L 20 A=EXP(-L) 30 S=1.0 40 RN=RND(1) 50 S=S*RN 60 IF(S-A)<0 THEN 90 70 X=X+1.0 80 GOTO 40 90 PRINT X Когда вероятность некоторого события для одного временного интервала такая же, как для любого другого, а осуществление какого-либо события не оказывает влияния на вероятность его повторного появления, имеется веское основание ожидать распределение Пуассона. Дополнительные основания для этого мы получаем, если в любом интервале времени имеет место высокая вероятность появления нулевого числа событий и если среднее число событий в каждом временном интервале мало. |