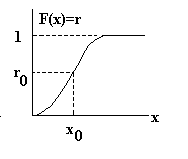|
6. Стандартные распределения случайных величин и их получение При рассмотрении дискретных или непрерывных случайных процессов вводят функцию F(x) , называемую кумулятивной функцией распределения величины X. Эта функция задает вероятность того, что случайная величина X принимает значение, не превосходящее числа х. Если случайная величина дискретна, т.е. X принимает конечное число значений, то функция F(x) является ступенчатой. Если F(x) непрерывна, то ее можно продифференцировать и получить функцию f(x)=dF(x)/dx. Функция f(x) называется функцией плотности вероятностей. Кумулятивную функцию распределения можно определить как F(x)=P(X<=x)=ò-¥xf(t)dt, (34) где F(x) изменяется на отрезке (0,1), а f(t) представляет собой значение функции плотности вероятностей случайной величины Х при X=t. Кумулятивная функция распределения дискретной случайной величины Х задается аналогично F(x) в виде F(x)=P(X<=x)=St=0xf(t), (35) где f(t)-частота или функция вероятностей, которая определяется для целых значений аргумента t по формуле f(t)=P(X=t), t=0, 1, 2,... (36) При генерировании случайных величин, имеющих различные функции распределения, в качестве исходного используются равномерно распределенные случайные величины. Их будем обозначить через r, 0 £ r £ 1, F(r)=r. Методы генерирования случайных величин равномерно распределенных на [0, 1] даны нами ранее в разделе 3. Если требуется генерировать случайные числа xi из некоторой статистической совокупности с функцией плотности вероятностей f(x), то сначала строят кумулятивную функцию распределения F(x)(рис. 14). 1. Строим график или таблицу интегральной функции распределения на основе ряда чисел, отражающих исследуемый процесс, значения случайной переменной откладываются по оси х, а значение вероятности (от 0 до 1) по оси у. 2. С помощью генератора случайных чисел выбираем случайное число в пределах от 0 до 1. 3. Проводим прямую до пересечения с кривой F(x) и снимаем значение х по оси х- оно берется как выбранное. 4. Повторяем процесс столько раз, сколько необходимо.
Рис. 14. Кумулятивная функция распределенияПусть имеем систему, в которой за каждый 10-минутный период число клиентов нуждающихся в обслуживании соответствует распределению, приведенному в табл. 6. Таблица 6
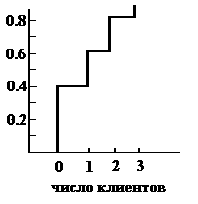
Предположим, что мы хотим провести эксперимент для 5 периодов времени. Строим график распределения кумулятивной вероятности (рис. 15).
Рис. 15. Распределение кумулятивных вероятностейГенерируем 5 двузначных целых чисел из интервала 00-99 и делим их на 100. Каждое из получившихся чисел используем для определения числа клиентов, появляющихся в данный момент времени. Если эти числа, например, равны 09, 54, 42, 80 и 20, то получаем следующую табл. 7. Таблица 7
Для непрерывной функции F(x), так как F(x) изменяется на промежутке [0,1], как показано на рис. 15, то чтобы получить случайные числа с этим распределением, можно также генерировать равномерно распределенные числа r и полагать F(х)=r. Величина х однозначно определяется из этого соотношения. Следовательно, для конкретного значения r, скажем r0, можно найти величину х, в данном случае х0, связанную с r0 обратной функцией к F х0=F-1(r0), (37) где F-1(r)-обратное отображение величины r, заданной на единичном интервале, в область изменения х. Математически этот метод можно выразить следующим образом: если мы генерируем равномерно распределенные случайные числа и ставим их в соответствие данной функции F(x),т.е. r=F(x)=ò-¥xf(t)dt, то P(X £ x)=F(x)=P[r £ F(x)]=P[F-1(r) £ x] (38) и, следовательно, F-1(r) есть случайная величина с функцией плотности вероятностей f(x). Это равносильно выражению величины х через значение r с помощью (37). Такая процедура называется методом обратного преобразования. |