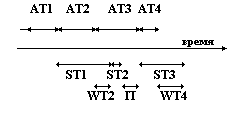
7.1. Элементарные сведения из теории массового обслуживания

Рассмотрим пример построения модели для системы массового обслуживания. Общим для таких моделей является необходимость пребывать в состоянии ожидания обслуживания. Феномен ожидания является следствием вероятностного характера возникновения потребностей в обслуживании и разброса показателей соответствующих обслуживающих систем. Ни время возникновения потребности в обслуживании, ни продолжительности обслуживания поступившего в обслуживающую систему клиента заранее не известно. Цель изучения режима функционирования обслуживающей системы при существенном факторе случайности состоит в том, чтобы взять под контроль количественные показатели функционирования системы массового обслуживания, например, среднего времени пребывания в очереди, времени простоя системы обслуживания из-за отсутствия заявок на обслуживание. Чем дольше ожидание, тем меньше простой и наоборот. Варьируя их, можно достигнуть компромисса. Рассматриваемые модели основаны на теории вероятности и теории случайных процессов. Взаимодействие заявки с обслуживающей системой рассматривается только с точки зрения регистрации продолжительности интервала времени, требуемого для полного обслуживания заявки с момента ее поступления в обслуживающую систему. Т.е. интерес представляют отрезки времени, разделяющие последовательные поступления заявок на обслуживание. При описании потока входящих требований используется распределение вероятностей моментов поступления требований и распределение времени обслуживания требований. При фиксированных параметрах потока требований, заявок, клиентов и заданном объеме обслуживающего оборудования длина очереди является функцией времени.

Поэтому процесс образования очереди будет стохастическим, так как он состоит из случайных событий. При построении функции распределения вероятностей для длины очереди нужно учесть особенности, присущие процессу образования очередей:

1) порядок, в соответствии с которым заказы поступают и занимают свое место в очереди;

2) количество обслуживающих единиц, исполняющих заказы и стратегию обслуживания, т.е. ограничения, наложенные на возможности и потребности обслуживания;

3) последовательность обслуживания - порядок очереди;

4) характер обслуживания и его длительность.

Cистемы массового обслуживания классифицируются с использованием обозначений Кендалла-Ли вида (a/b/c):(d/e/f),

где символы a, b, c, d, e, f связаны с существенными элементами модельного представления процессов массового обслуживания.

a-распределение моментов поступления заявок на обслуживание, b- распределение времени обслуживания (или выбытий обслуженных клиентов), с- число параллельных узлов обслуживания, d – дисциплина очереди, e- максимальное число допускаемых в систему требований (число требований в очереди + число требований, принятых на обслуживание), f- емкость источника, генерирующего заявки на обслуживание. Для a и b приняты следующие обозначения:

М- пуассоновское распределение моментов поступлений заявок на обслуживание или выбытий из системы обслуженных клиентов (или экспоненциальное распределение интервалов времени между моментами последовательных поступлений или продолжительностей обслуживания клиентов),

D- фиксированный (детерминированный) интервал времени между моментами последовательных поступлений в систему заявок на обслуживание или детерминированная (фиксированная) продолжительность обслуживания,

E_k- распределение Эрланга или гамма-распределение интервалов времени между моментами последовательных поступлений требований в обслуживающую систему или продолжительностей обслуживания (при этом k –параметр распределения),

GI- распределение произвольного вида моментов поступления в систему заявок на обслуживание (или интервалов времени между последовательными поступлениями требований),

G- распределение произвольного вида моментов выбытия из системы обслуженных клиентов (или продолжительностей обслуживания).

Например, (M/D/10):(GD/N/¥) означает систему массового обслуживания с пуассоновским входным потоком, фиксированным временем обслуживания и 10 параллельными узлами, дисциплина очереди не регламентирована, независимо от числа поступающих требований данная система (очередь +обслуживаемые клиенты) не может вместить более N требований, т.е. остальные не принимаются, источник ¥ емкости.

При решении такого сорта задач возможны две ситуации:

1) число заказов слишком велико, что приводит к большому времени ожидания в очереди и говорит о недостаточном количестве станций обслуживания;

2) недостаточное число заказов, что приводит к большому времени простоя оборудования и говорит об избытке оборудования.

Поскольку оба требования являются взаимоисключающими, то целью решения задачи являются установление оптимального соотношения между потерями, вызванными простоем оборудования и потерями из-за ожидания в очереди.

Примером, который часто приводится в литературе, служит моделирование системы массового обслуживания с одной станцией обслуживания, обслуживание в порядке поступления, время обслуживания и время между поступлениями распределены по экспоненциальному закону. Если мы возьмем некоторый интервал времени между поступлениями i-го и (i+1) требований и обозначим его ATi, а время обслуживания i-го требования –STi, то время ожидания (WTi) и простой станции (IT) можно изобразить графически, как это сделано на рис. 20.

Рис. 20. Одноканальная система массового обслуживания

Рассмотрим самый простой вид потока заявок - стационарный пуассоновский поток, который имеет свойства стационарности, ординарности и отсутствия последействия. Поток является стационарным, если его вероятностные характеристики не зависят от сдвига во времени, т.е. вероятность, что на интервале t происходит некоторое количество событий, зависит от длины интервала и не зависит от его положения на оси t. Поток является ординарным, если в каждый момент времени может поступать только одна заявка. Отсутствие последействия означает независимость событий друг от друга, т.е. длина интервала времени до момента поступления следующей заявки не зависит от того, поступила ли в начале этого интервала заявка или нет.

Рассмотрим процесс образования очереди на единственной станции- найдем среднюю длину очереди и вероятность появления очереди заданной длины при случайных потоках заказов. Пусть скорость обслуживания не зависит от числа заказов в очереди и заказы обслуживаются по очереди. Используем следующие обозначения:

P_n(t)- вероятность образования очереди из n заказов к моменту t,

lDt- вероятность появления в очереди нового заказа в промежутке времени от t до t+Dt, где l - средняя скорость появления заказов,

mDt-вероятность того, что в интервале времени от t до t+Dt завершается исполнение заказа, находящегося на обслуживании, где m- средняя скорость обслуживания,

L_s-среднее число находящихся в системе клиентов (заявок)

L_q-среднее число клиентов в очереди на обслуживание

W_s- средняя продолжительность пребывания клиента в системе

W_q- средняя продолжительность пребывания клиентов в очереди.

По определению [11]

L_s=S_n=0^¥ np_n, L_q==S_n=c^¥ (n-c)p_n, где с- число узлов обслуживания.

Между L_s и W_s (L_q и W_q) существует строгая взаимосвязь. В частности, если частота поступлений в систему заявок равна l, то

L_s=lW_s, L_q=lW_q.

Если не все заявки могут попасть в блок ожидания, то вводят l_эфф, учитывающее действительно допускаемые в систему требования, т.е. эффективная частота поступлений. Тогда L_s=l_эффW_s, L_q==l_эффW_q

В общем случае l_эфф=bl, 0<b<1. В любом случае можно установить зависимость от L_s и L_qдля l_эфф. По определению средняя продолжительность пребывания в системе равна средней продолжительности пребывания требований в очереди плюс среднее время обслуживания. Если средняя скорость обслуживания-m и средняя продолжительность обслуживания 1/m, то W_s=W_q+1/m. Умножая на l, получаем L_s=L_q+l/m. Это справедливо и для l®l_эфф. При этом l_эфф=m(L_s-L_q). Далее основное внимание будет направлено на формулы для P_n , так как из них можно получить все остальные в следующей очередности

P_n®L_s=S_n=0^¥ np_n®W_s=L_s/l®W_q=W_s-1/l®L_q=lW_q.

Рассмотрим пример, пусть с=1 и среднее количество поступлений -3 в час, а скорость обслуживания –8 в час. Вероятность того, что в системе окажется n требований-Pn определяется на основе наблюдений и данные помещены в табл. 11.

Таблица 11

n	0	1	2	3	4	5	6	7	³8
Pn	0.615	0.234	0.088	0.033	0.012	0.005	0.002	0.001	0

Вычислим L_s, W_s, W_q, L_q.

L_s=S_n=0^¥ np_n=0*0.625+1*0.234+2*0.088+3*0.033+4*0.012+5*0.005+6*0.002+

+7*0.001==0.6 требования. Так как l=3, то W_s=L_s/l=0.6/3=0.2 часа. Учитывая, что m=8, имеем W_q=W_s-1/m=0.2-1/8=0.075 часа, т.е. среднее количество находящихся в очереди клиентов равно L_q=lW_q=3*0.075=0.225.

Вычислите среднее количество находящихся в очереди требований , используя Pn- ответ L_q==S_n=2^¥ (n-1)p_n=0.225.

Вычислите среднее количество клиентов, которое обслуживается системой –ответ L_s-L_q=l/m=0.375.

В теории массового обслуживания показано, что поведение вероятности P_n(t) будет описываться дифференциальными уравнениями

dP_n(t)/dt=lP _n-1(t)+mP _n+1(t)-(l+m)P_n(t), (n>0)

dP₀(t)/dt= -lP₀(t)+mP₁(t) (51)

Они в неявном виде отражают связь между временем ожидания и временем обслуживания и являются исходным пунктом для решения задач теории очередей. В частном случае P_n(t)=P_n=const решение имеет простой вид

P₀=1-(l/m), P_n=(l/m)ⁿ(1-l/m) , (52)

где Р_n -вероятность появления очереди длины n. Отношение l/m называется интенсивностью нагрузки – средний объем обслуживания в единицу времени. Для среднего числа находящихся в системе клиентовполучается формула

L_s==S_n=0^¥ np_n =(l/m)/(1-l/m), l/m<1. (53)

Пусть число поступающих заказов в день равно l=10, а скорость обслуживания m=20 заказов в день. Тогда l/m=1/2. Подставляя это значение в формулы, получим

P_n=(1/2)ⁿ(1-1/2) и L_s=(1/2)/(1-1/2)=1 (54)

Тогда вероятность появления очереди из 0,1,2… заказов в любой момент времени будет иметь вид табл. 12

Таблица 12

N	0	1	2	3
P_n	1/2	¼	1/8	1/16

С увеличением интенсивности нагрузки l/m средняя длина очереди быстро возрастает и при l/m->1 становится бесконечной. Уравнение для n перестает быть справедливым при l/m=1. Подставляя несколько значений l/m в формулу, можно найти как изменяется средняя длина очереди в зависимости от l/m (табл. 13).

Таблица 13

Интенсивность нагрузки	½	¾	7/8	15/16
Средняя длина очереди	1	3	7	15

Обозначим r=l/m, тогда W_s=1/[m(1-r)], L_q=r²/(1-r), W_q=r/[m(1-r)].

Рассмотрим пример, пусть на мойку автомобили поступают по закону Пуассона со средней интенсивностью 5 автомобилей в час. Продолжительность обслуживания подчиняется экспоненциальному закону со средним значением 10 автомобилей в час. Узел обслуживания один. Таким образом l=5, m=60/10=6 автомобилей в час, таким образом, r=l/m=5/6<1 и достигается стационарный режим. Вычислим, какое количество стоянок нужно оборудовать на мойке.

L_q=(5/6)²/(1-(5/6))=4.14»4 автомобиля. Но L_q-это математическое ожидание, т.е. может быть больше или меньше этого количества. Допустим, цель обеспечить одновременно 80% клиентов стоянкой. Это эквивалентно выполнению условия p₀+p₁+…+p_s³0.8. Используя формулу для p_n, можно записать (1-r)+(1-r)r+…+(1-r)r^s³0.8. Учитывая, что

(1-r)+(1-r)r+…+(1-r)r^s=(1-r)(1+r+…+r^s)= (1-r)[(1-r^s+1)/(1-r)]=(1-r^s+1),

получаем r^s+1£0.2. Логарифмируя при r=5/6, имеем (s+1)log(5/6)£log0.8.

Так как log(5/6)<0, то деление на log(5/6) меняет знак неравенства, т.е. для s получаем s³log0.2/log(5/6)-1=7.8»8 площадок. Можно вычислить долю времени бездействия мойки – вероятность того, что на мойке не окажется ни одного автомобиля p₀=1-r»0.17, т.е. 17% времени простаивает. Для оценки качества обслуживания полезно знать среднее время пребывания автомобиля на станции (от момента прибытия до момента завершения мойки)=W_s=1/[m(1-r)]=1/[6(1-5/6)]=1 час.

Вычислите вероятность то, что прибывший автомобиль будет ждать обслуживания- ответ 0.8333.

Вычислите вероятность того, что при наличии 6 мест для стоянки для прибывающего автомобиля не найдется места –ответ p _n³7=r⁷=0.279.

Для системы массового обслуживания вида (M/M/1): (GD/N/¥) для вероятностей были получены следующие формулы

P_n=[(1-r)/(1-r^N+1)]rⁿ, для r¹1 и n=0, 1,…N

P_n=1/(N+1) для r=1.

L_s=[r{1-(N+1)r^N+Nr^N+1}]/[(1-r)(1-r^N+1)] для r¹1

L_s=N/2 для r=1.

Рассмотрим пример, пусть мойка имеет 5 площадок для стоянки. Службу интересует количество клиентов, которое она теряет из-за ограниченности числа площадок. Это эквивалентно нахождению разности между l и l_эфф.

l_эфф=l(1-p_N), откуда l-l_эфф=lp_N_.Здесь N=5+1=9, r=5/6 и p_N=[(1-(5/6))/(1-(5/6)⁷](5/6)⁶=0.07774, N=6, т.е. частота возникновения ситуаций, когда все 5 стоянок заняты, равна 5*0.07774=0.387 автомобилей в час, при 8-часовом рабочем дне это означает потерю 3 клиентов в среднем. Определим среднее время пребывания на мойке, вычислив L_s и W_s.

L_s={(5/6)[1-7*(5/6)⁶+6(5/6)⁷]}/{(1-5/6)[1-(5/6)⁷]}=2.29 автомобиля.

Так как вероятность того, что требования не имеют возможности присоединиться к очереди равна p_N (т.е. вероятности, что в системе уже N требований) доля требований, которым разрешено войти в блок ожидания равно P{n<N}=1-p_N_.Отсюда l_эфф=l(1-p_N), W_q=L_q/l_эфф=L_q/l(1-p_N), L_s=L_q+l_эфф/m=L_q+l(1-p_N)/m, W_s=W_q+1/m=L_s/l(1-p_N). Таким образом, l_эфф=m(L_s-L_q)=l(1-p_N). С учетом l_эфф=l(1-p₆)=5(1-0.07774)=4.613, получаем W_s=L_s/l_эфф=2.29/4.613=0.496 часа. Таким образом, при введении ограничения на количество мест для стоянки (N=6) среднее время ожидания сократилось на полчаса по сравнению с ¥ очередью. Это достигнуто за счет «потери» в среднем 3 автомобилей в день из-за недостаточности мест для стоянки.