|
7.3. Имитация задач теории массового обслуживания Раccмотрим одноканальную однофазовую модель. В ней система состоит из одной станции, на которую поступают заявки, образующие очередь. Если станция свободна, то она приступает к обслуживанию той заявки из очереди, которая стоит первой. Промежуток времени между появлениями двух последовательных заявок и время обслуживания считаются случайными величинами с заданными функциями распределения. Введем следующие обозначения WT- среднее время ожидания заявки в очереди IDT- среднее время простоя системы в ожидании очередного требования WTi-время ожидания i-ой заявки IDTi-время простоя системы в ожидании i-той заявки ATi-интервал между появлениями i-той и i+1-ой заявками Sti-время обслуживания i-той заявки, i=1,2,3,…m F(AT)-функция распределения плотности вероятностей интервала времени между двумя последовательными заявками F(ST)-функция распределения плотности вероятностей времени обслуживания. WT=1/mSi=1mWTi=TWT/m, IDT=1/mSi=1m IDTi=TIDT/m (58) Блок-схема программы приведена на рис. 22. В блоке 1 обнуляется время появления первой заявки, время ее ожидания, время простоя системы в ожидании ее прихода, полное время ожидания и простоя и фиксируется факт появления первой заявки. Блок 2 генерирует относительное время появления следующей заявки. Оно отсчитывается от момента прихода предыдущего требования. В блоке 3 из полученной величины отнимается время ожидания предыдущей заявки. Эта разность определяет новое значение относительного времени прибытия нового требования. Его отсчет ведется теперь от момента начала обслуживания
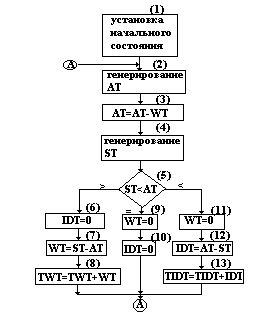
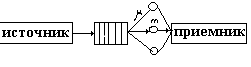
Рис. 22. Блок-схема расчетов по одноканальной однофазовой модели массового обслуживания Рассмотрим работу многоканальной системы массового обслуживания с неограниченной очередью (рис. 23) [18]
В данной системе возможны два события: 1) поступление заявок из источника на обслуживание (если один из приборов свободен), либо в очередь; 2) окончание обслуживания очередной заявки, поступление ее на приемник и выбор следующей заявки из очереди (если очередь не пуста). Блок управления моделью определяет, какое из событий настанет раньше и присваивает системному времени значение, равное времени наступления этого события. Затем управление передается на блоки, имитирующие работу отдельных устройств, и выполняются действия, связанные с данным событием. Например, при поступлении очередной заявки из источника необходимо: 1) сгенерировать время поступления следующей заявки; 2) если все каналы заняты - увеличить длину очереди на одну заявку; 3) если есть свободный прибор, то пометить его как занятый и сгенерировать время окончания обслуживания заявки. Обозначим t - модельное время, n - длина очереди, k – число занятых каналов,m – общее число каналов, ns- число обслуженных заявок, a- псевдослучайная величина, распределенная равномерно на отрезке [0,1], tp- время поступления очередной заявки в систему, ts[1:m]- упорядоченный по возрастанию массив времен окончания обслуживания заявок на занятых каналах, n1 и n2 - первый и второй моменты распределения длины очереди. Считаем, что время между поступлением заявок распределено экспоненциально с параметром l, а время обслуживания также распределено экспоненциально с параметром m. Моделирование прекращаем после обслуживания 10 заявок. По определению, первый и второй моменты распределения длины очереди равны n1=Si=0¥ i*P(n =i); n2 = Si=0¥ i2*P( n=i), (59) где P(n=i) –вероятность того, что длина очереди равна i. В качестве оценки вероятности P(n=i) будем использовать отношение времени, которое длина очереди была равна i , к общему времени моделирования. Для исходных данных l=5, m=2, m=3 блок-схема алгоритма приведена на рис. 24.
Задачи для самостоятельной работы
1. Время между последовательными прибытиями покупателей равномерно распределено в интервале от 1 до 20 минут. Для 50 % покупателей время обслуживания -8 минут, для остальных-14 минут. Какие генераторы нужно взять? Определите суммарное время ожидания покупателей и время простоя системы за 4 часа работы магазина. 2. По блок-схеме рис. 25 напишите программу и определите вероятности P(n=i), n1 и n2. Постройте таблицу значений t, tp, ts(1), ts(2), ts(3), k, n, ns и график зависимости n от t. 3. Имеется одноканальная СМО с очередью ограниченной длины. Время между поступлением заявок распределено равномерно на отрезке [0,2], время обслуживания имеет экспоненциальное распределение с параметром m=1. Длина очереди n=1. Если очередь заполнена, то поступившее вновь требование покидает СМО без обслуживания. Моделирование закончить после обслуживания заданного числа заявок. Построить заданные характеристики для длины очереди. 1. Имеем многоканальную СМО с отказами без очереди. Если все каналы заняты, заявка, вновь поступившая в систему, покидает систему без обслуживания. Время между поступлением заявок распределено экспоненциально, с параметром l=1. Количество каналов m=2. Время обслуживания заявок на каждом приборе распределено равномерно на отрезке [0, 1]. Моделирование закончить при достижении заданного модельного времени Т. Постройте заданные характеристики для количества занятых каналов. Блок – схемы алгоритмов для решения этих задач можно найти в [16, 17].
|