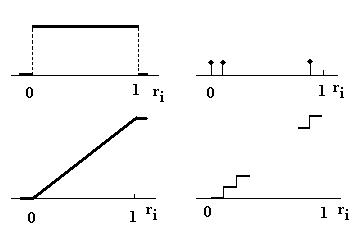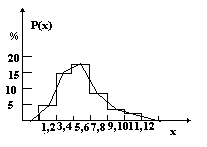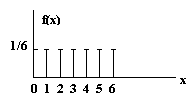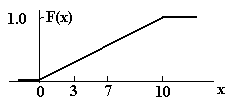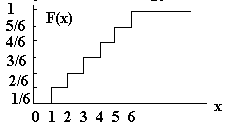Приложение

Элементы теории вероятности и математической статистики

Случайность и вероятность

В жизни не все события строго детерминированы, т.е. нельзя заранее точно сказать, что какое-то событие свершится. Описанием таких событий занимается теория вероятностей и математическая статистика. Чтобы определить понятие вероятности случайного события, введем понятие исхода, пространства событий и события. С точки зрения теории вероятностей эксперимент представляет собой «действие», результат которого изменяется случайным образом. В зависимости от природы эксперимента число результатов эксперимента - исходов может быть конечным или бесконечным. Например, бросая игральную кость, мы имеем возможность 6 исходов. Пространством событий называется множество всех возможных исходов эксперимента. Для кости это {1, 2, 3, 4, 5, 6}.

Событие - совокупность исходов, принадлежащих пространству событий. Можно, например, рассматривать событие, состоящее в том, что при бросании кости выпадет 6. В этом случае наступление такового события соответствует исходу 6. Если событие состоит из того, что при двух бросаниях сумма очков будет равна 5, то оно реализуется всякий раз, когда двумя последовательными исходами являются (4, 1), (3, 2), (2, 3) и (1, 4).

Вероятность некоторого события Е, обозначаемая как P{E}, представляет собой неотрицательное действительной число, не превосходящее 1, равное доле испытаний (при большом их числе), исходы которых совпали с Е. Если n - общее число испытаний (экспериментов), а m - число экспериментов, исходом которых явилось событие Е, то вероятность P {E} определится как

P{E}=lim _n®¥m/n и 0£P{Е}£1

При P {E} = 0 событие невозможно, при P {E} = 1 оно достоверно.

Для вероятностей доказаны следующие законы.

Закон сложения вероятностей

P {E+F} = P {E} + P {F} - P {EF} (1)

Здесь обозначено P {E+F} = P {EÈF} - вероятность реализации или E, или F (объединение E и F), P {EF} = P {EÇF} - вероятность реализации обеих событий одновременно (пересечение E и F).

Согласно закону сложения вероятность E или F равна вероятности E плюс вероятность F минус вероятность E и F.

Если события E и F взаимно исключаются, т.е. наступление одного означает отсутствие другого, то P {EF} = 0. В этом случае

P {E + F} = P {E} + P {F}

Закон условной вероятности определяет вероятность события E при условии наступления события F.

P {E/F} = P {EF}/ P {F}, P {F}>0 (2)

Два события E и F называются независимыми, если P {E/F} = P {E}, таким образом из закона (2) следует, что E и F независимы, когда

P {EF} = P {E} P {F}, т.е. вероятность одновременного наступления событий равно произведению вероятностей событий E и F.

Случайные величины и распределение вероятностей

Исходы эксперимента представляют собой случайные величины, если им можно приписать значения действительных чисел. Для бросания костей соответствующие случайные величины представляют собой множество исходов 1, 2, 3, 4, 5, 6. Для бросания монеты исходы орел и решка можно представить в виде случайной величины, приписав значение 0 исходу орел и значение 1 - решке. Таким образом, в некотором смысле можно считать случайную величину функцией, принимающей действительные значения и отображающей пространство событий на действительную прямую.

Случайная величина может быть дискретной или непрерывной. Дискретная принимает определенные значения в отдельных точках прямой, непрерывная - любые значения на некотором непрерывном отрезке прямой (рис. 28).

Какими параметрами можно охарактеризовать случайную величину? Допустим, фирма решила изучить то, как сотрудники пропускают работу в течение года. Пусть для 50 сотрудников получены следующие данные за год

563795645615647443967385645515358872413435009 12 2478

В общем случае это случайная величина, которая принимает дискретные значения. Полученные данные являются сырыми, неклассифицированными. В таком виде они неудобны для того, чтобы изучить характеристики случайной величины. Их представление можно улучшить, упорядочивая их по величине от минимального значения 0 до максимального 12.

число дней пропусков 0 1 2 3 4 5 6 7 8 9 10 11 12

число исходов 2 3 2 6 8 10 7 7 3 4 0 0 1, всего 50

Для построения графика данные нужно разбить на классы, для определения необходимого числа классов используют эмпирическую формулу

m = 1 + 3.3 log N,

где m - число классов, N - полное число членов в распределении.

Рис. 28. Распределение непрерывной и дискретной случайной величины и их кумулятивные вероятности

Для нашего случая имеем:

m = 1 + 3.3 * (log 50) = 1 + 3.3 * 1.7 = 6.6, т.е. нужно разбить на 6 - 7 классов. Разобьем промежуток от 0 до 12 на следующие классы и одновременно запишем число служащих в каждом классе

1 - 2 5

3 - 4 14

5 - 6 17

7 - 8 9

9 - 10 4

11 и выше 1

Собранные данные обычно суммируются в виде распределения относительных частот (гистограммы), такая гистограмма приведена на рис.

29. Если мы имеем дело с дискретной переменной, то записываем частоты появления каждого из ее возможных значений. Если переменная непрерывная, разбиваем весь диапазон ее значений на равные интервалы (группы) и записываем частоты появления каждой группы. Тогда относительная частота для каждой группы равна частному от деления наблюдаемого числа событий данной группы на общее число событий.

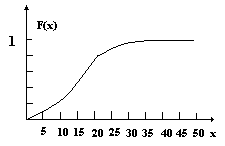
Рис. 29. Гистограмма распределения пропусков сотрудников

Построим кумулятивное распределение суммированием пропусков служащих, которое примет вид рис. 30.

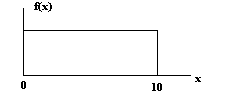
Рис. 30. Кумулятивная функция

Часто требуется выразить общие характеристики распределения вероятностей через некоторые рациональные меры, по которым можно сделать выводы о свойствах случайной величины. Этими мерами являются математические ожидания определенных функций от рассматриваемой случайной величины. Пусть х – случайная величина, а h(x) – некоторая функция от х. Назовем F{h(x)} математическим ожиданием значения h(x) по отношению к распределению вероятностей х. Тогда

E{h(x)}= ò_-¥^¥h(x)f(x)dx, х – непрерывная величина

=S_x h(x)P(x), х –дискретная величина.

Для общей характеристики свойств одномерной случайной величины обычно используются две меры. Это математическое ожидание E{x} или m и дисперсия или среднеквадратическое отклонение s. Математическое ожидание является мерой положения распределения относительно начала координат, а дисперсия- мерой разброса распределения относительно его математического ожидания. Подставляя h(x) =x в определение, имеем

E{x}=ò_-¥^¥xf(x)dx=ò_-¥^¥xdF(x), х –непрерывная величина

= S_x xP(x), х- дискретная величина.

Когда экспериментальные данные разбиты на группы, среднее (математическое ожидание) и дисперсию можно вычислить по формулам

Среднее=m=S_i=1^kM_iF_i/n

Дисперсия=s=(S_i=1^kM_i²F_i-nm²)/(n-1),

где n- полный объем выборки, n=S_i=1^kF_i;

k- число групп (интервалов);

M_i-средняя точка i-го интервала или ( для дискретных данных ) значение i-й группы;

F_i-частота появления i-й группы или i-го интервала.

Для нашего примера имеем

m=263/50=5.3

s=s²=1/49(3*1+2*4+6*9+8*16+10*25+7*36+6*49+3*64+4*81+144)-263/(50*49)=5.421

Чем меньше дисперсия в данных, тем более представительно среднее для всех членов в распределении.

Со случайной величиной x связывают также функцию f(x), которую можно использовать, чтобы поставить в соответствие этой величине некоторую вероятностную меру. Эту функцию называют плотностью распределения вероятностей.

Если x представляет собой непрерывную случайную величину, заданную на интервале (- ¥, + ¥) , то f(x) должна удовлетворять условиям f(x)³0 и

ò_-¥^¥f(x)dx=1

Если x - дискретная случайная величина, то ее плотность вероятности P(x), определяющая вероятность, что x примет некоторое заданное значение, должна удовлетворять условиям: P(x)³0 для всех x и S_xP(x)=1.

Рассмотрим примеры.

Если f(x)=a при 0<x<10, иначе 0, то

график функции f(x) будет иметь вид рис. 31.

Рис. 31. Вид графика f(x)

Таким образом, чтобы она была плотностью вероятности, должно быть выполнено условие: ò₀¹⁰adx=1=ax|₀¹⁰=10a

откуда: a=1/10, так как a > 0, то f (x) ³ 0.

Пример 2

Вероятность выбросить кость P (x) = 1/6 для x = 1, 2, 3, 4, 5,6.

Тогда график функции примет вид рис. 32.

Рис. 32. Вид графика функции f(x)

Другой полезной мерой вероятности является распределение вероятностей случайной величины или кумулятивная вероятность. Пусть F (x) есть распределение вероятности непрерывной случайной величины x, - ¥ <x <¥. Тогда для любого a функция F(a) определяет вероятность того, что x £ a через плотность вероятности f(x)

F(a)=P{x<a}=ò_-¥^af(x)dx

Следовательно, F(a) есть площадь под кривой f(x) на интервале - ¥ <x < а. Функция распределения вероятностей F(a) обладает следующими свойствами:

lim_a_®¥F(a)=lim_a_®¥ò_-¥^af(x)dx=1

lim_a_®-¥F(a)=lim_a_®-¥ò_-¥^af(x)dx=0

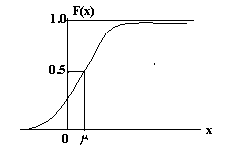
Типичная функция распределения имеет вид (рис. 33).

Рис. 33. Распределение вероятности (кумулятивная функция)

Ордината функции F(x) непосредственно определяет вероятность того, что x меньше некоторого фиксированного значения.

Из соотношения f(x) и F(x)следует, что:

f(x)=dF(x)/dx

Таким образом, закон распределения вероятностей случайной величины x полностью определяется либо f(x), либо F(x). Для дискретного случая нужно заменить f(x) на P(x) везде и перейти к суммам, а дифференцирование заменить конечными разностями.

Распределение вероятностей случайной дискретной величины имеет вид ступенчатой функции, так как плотность вероятности определена только для дискретных значений.

Пример 3. Для плотности вероятности в непрерывном случае

F(x)=1/10 при 0<x<10 и 0 –иначе.

Функция распределения на интервале 0 £ x £ 10 определится следующим образом

F(x)=ò₀^xf(u)du=ò_o^x(1/10)du=x/10, 0<x<10.

Ёе график представлен на рис. 34.

Рис. 34. График функции F(x)

Для дискретной случайной величины x с плотностью вероятности, задаваемой табл. 14

Таблица 14

X	1	2	3	4	5	6
P(x)	1/6	1/6	1/6	1/6	1/6	1/6

имеем:

F(x)=S_u=1^u=x1/6=x/6 для x=1,2,3,4,5,6,

отсюда имеем следующий рис. 35.

Рис. 35. График функции F(x).

Различные виды распределения вероятностей

1. Дискретное распределение вероятностей

Простейший вид плотности вероятности получается в результате реализации схемы независимых испытаний Бернулли. Испытание Бернулли имеет два исхода: 0 или 1. Пусть случайная величина принимает два значения 0 или 1. Соответствующую плотность вероятности можно записать так

P{x=0}=p и P{x=1}=q=1-p, где 0<q<1.

Рассмотрим случай n независимых испытаний Бернулли, в которых p - постоянно.

Вероятность определенной комбинации исходов с k неудачами и (n-k) успехами равно p^kq^k (0 £ k £ n) согласно закону независимых испытаний. Например, для n=5 вероятность того, что исходом первого испытания будет неудача, а остальными - успех, будет pq⁴. Рассмотрим вероятность того, что число неудач в n независимых испытаний равно k, где n - фиксировано. При вычислении данной вероятности необходимо учитывать все различные состояния, в которых зафиксировано k неудач (независимо от порядка их появления в n испытаниях). Существует (ⁿ_k)=n!/(n!(n-k)!) различных сочетаний. Поскольку вероятность появления каждой комбинации равна p^kqⁿ^-k, то по закону сложения вероятностей получаем:

P{x=k}=(ⁿ_k)p^kqⁿ^-k , k=0,1,2,…n

Это соотношение называется биноминальным распределением с параметрами n и p. Оно удовлетворяет определению плотности вероятности, так как P {x=k} ³ 0 для всех k = 0, 1, 2, ...n

и S_k=0ⁿP{x=k}=S_k=0ⁿ(ⁿ_k)p^kqⁿ^-k=(p+q)ⁿ=1

2. Отрицательное биноминальное распределение (Паскаля)

Значение вероятности случайной величины определяется числом независимых испытаний, при котором происходит фиксированное число неудач. Пусть j и c –число испытаний и фиксированное число неудач. Вероятность того, что при j испытаниях будет иметь место c неудач, является произведением двух вероятностей: вероятности (с-1) неудач в (j-1) испытаний равной (^j-1_c-1)p^c^-1 q^j^-c и вероятности неудачи в j-м испытании равной p. Плотность вероятности описывается выражением

P{x=j}= (^j-1_c-1)p^c q^j^-c , j=c, c+1, c+2…

3. Частным случаем распределения Паскаля является геометрическое распределение, получаемое при с=1, т.е.:

P{x = j} = p q^j^-1, j = 1,2,3...

оно описывает время, протекающее до наступления определенного числа неудач.

4. Распределение Пуассона

Рассмотрим случайную величину x, принимающую только целые, больше нуля значения k = 0, 1, 2 ... Распределение с плотностью

P{x = k} = l^kе^-l/k!, k = 0, 1, 2,....,

где l > 0, называется распределением Пуассона и часто используется в теории массового обслуживания. Допустим, что в биноминальном распределении p ® 0, n ® ¥ так, что np ® l > 0. Тогда плотность вероятности биноминального распределения станет

P{x=k}=(ⁿ_k)(l/n)^k(1-l/n)^n-k®(l^kе^-l)/k!

Можно показать, что при n ® ¥ это выражение стремится к распределению Пуассона. Таким образом, если n велико, а p мало, так что l = np > 0, пуассоновское распределение аппроксимирует биноминальное.

Непрерывные распределения вероятностей

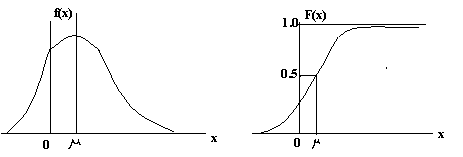
5. Нормальное распределение вероятности имеет плотность, определяемую формулой

f(x)=(1/Ö2ps²)exp(-(x-m)²/2s²⁾,-¥<x<¥

где m и s - заданные параметры.

Соответствующая формула распределения имеет вид:

F(x)=ò_-¥^¥(1/Ö2ps²)exp(-(y-m)²/2s²)dy

Типичные графики f(x) и F(x) показаны на рис. 36.

Рис. 36. Вид графиков f(x) и F(x)

Функция f(x) симметрична относительно x = m.

Выражение F(x) табулировано на основании стандартного нормального закона распределения вероятностей с плотностью

j(z)=(1/Ö2p)exp(-z²/2), -¥<z<¥

и параметрами m = 0 и s = 1. Cоответствующая функция распределения имеет вид

F(z)=ò_-¥^¥(1/Ö2p)exp(-y²/2)dy.

Путем подстановки z = (x-m) / s нормальное распределение с произвольными параметрами x и s сводится к стандартному виду. Нормальное распределение можно аппроксимировать к биноминальному виду. Можно показать, что при заданном фиксированном p и n ® ¥

S_k=a^b(ⁿ_k)p^kq^n-k®1/(Ö2p)ò _(a-_m-1/2)^(b-m+1/2)exp(-y²/2)dy,

где: m = np и s=Önpq.

6. Экспоненциальное распределение, плотность которого выражается формулой

f(x) = m e^-
mx, x>0

где m > 0 - заданный параметр, и имеет график плотности вида рис. 17. Экспоненциальное распределение для непрерывного случайного аналогично геометрическому для дискретного случая. Если в геометрическом распределении случайная величина представляет число испытаний до первого отказа, то в экспоненциальном в непрерывном случае соответствующим аналогом будет промежуток до первого отказа. Можно доказать, что при p ® 0 и времени испытания t® 0 геометрическое распределение в пределе стремится к экспоненциальному. Если случайная величина, подчиняющаяся закону Пуассона, представляет число отказов в единицу времени, то случайная величина, распределенная по экспоненциальному закону, определяет промежуток времени между двумя последовательными отказами.

5. Гамма – распределение

Сумма n независимых случайных величин, распределенных по одному и тому же экспоненциальному закону, описывается гамма - распределением (Эрланга), плотность которого определяется формулой

f(x)=[m(mx)^n-1 e^-mx]/(n-1)!, x>0

При n = 1 эта формула сводится к плотности экспоненциального распределения.