2.3. Понятие о нечетком выводе

До сих пор мы считали, что каждое правило работает всегда и каждый факт либо абсолютно истинен, либо абсолютно ложен. Но на практике не всегда такая модель себя оправдывает, так иногда удобнее считать некоторые факты применимыми с какой-то вероятностью, так возникает стохастическая (вероятностная) модель.
Пример.
F(Иван, Серж)  - 80 % - 0,8. Иван – отец Сержа с вероятностью 80%.
F(Серж, Алекс) – 90% - 0,9. Серж – отец Алекса с вероятностью 90%
F(X,Y) ÙF(Y,Z) →GF(X,Z) – 100% - 1
Цель(терминальное условие) – GF(Алексей, Сергей).
В данном случае мы нельзя дать утвердительный или отрицательный ответ на запрос, а можно только оценить вероятность – имеет ли место требуемый факт.
Так в данном примере, очевидно, что GF(Алексей, Сергей) с вероятностью 0,9*0,8=0,72; т.е. верно на 72%.
Решение подобных задач называется нечетким выводом. Нечеткий вывод широко применяется при проектировании экспертных систем, решении задач распознавания образов и т.д.
Пример. Распознавание почтовых индексов.
Почтовый индекс состоит из семи типовых линий (рис. 2.4.).

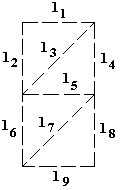
Рис. 2.4. Почтовый индекс

После сканирования индексов, тем или иным способом вычислена вероятность того, что проведена та или иная линия p(l1),…,p(l7). Тогда можно вычислить вероятность наличия каждой цифры p(0),…., p(9).
С учетом следующего образца (рис. 2.5.), можно задать правила следующего вида.

Рис. 2.5. Образец заполнения почтового индекса

l3 Ù l4 Ù l8   → 1      0,97               (1)
l3 Ù l4          → 1      0,75               (2)
l4 Ù l8         → 1       0,6                 (3)
l3 Ù l8         → 1        0,5                (4)
Пусть:
p (l3) = 0,9         p (l4) = 0,9               p(l8) = 0,95,
тогда:
по первому правилу:
p(1) = 0,9 ∙ 0,9 ∙ 0,95 ∙ 0,97 = 0,95 ∙ 0,81 ∙ 0,97 ≈ 0,75
по второму правилу:
p(1) = 0,9 ∙ 0,9 ∙ 0,75 = 0,81 ∙ 0,75 ≈ 0,6
по третьему правилу:
p(1) = 0,9 ∙ 0,95 ∙ 0,6 = 0,54 ∙ 0,95 ≈ 0,51
по четвертому правилу:
p(1) = 0,9 ∙ 0,95 ∙ 0,5 ≈ 0,43
Таким образом
p(1) = 0,75  (определяется по максимуму)
За истинный принимается наиболее вероятно-распознанный символ, например, в том случае, если его вероятность превышает определенный порог.