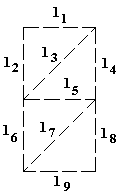3.4. Понятие о нечетком выводе на продукциях

В продукционных моделях, также как и в логических, существует возможность организации нечеткого вывода.
Если в обычных детерминированных моделях предполагается, что каждое правило является либо применимым или неприменимым, то в нечетких моделях для каждого состояния задана таблица вероятностей применения тех или иных правил. Можно высчитать вероятности достижения целей с помощью применения определенных последовательностей правил, можно определить самое вероятное решение, или найти решение, удовлетворяющее заданному вероятностному порогу (p>a, 0<=a<=1).
Пример. Опишем на продукциях задачу распознавания почтовых индексов (задача, аналогичная описанной в 2.3).
Предположим, что после сканирования получаем данные о том, с какой вероятностью какие линии проведены (шаблон на рис ?).

Рис. 3.1. Почтовый индекс

Сформулируем, например, следующие правила.
l3, l4, l8 → 1    0,97     (1)
l3, l4     → 1    0,75      (2)
l4, l8     → 1    0,6       (3)
l3, l8     → 1    0,5       (4)
Терминальные условия соответствуют цифрам от 0 до 9. Результат распознавания – наиболее вероятный символ, если его вероятность превышает определенное пороговое значение.
Пусть:
p (l3) = 0,9         p (l4) = 0,9               p (l8) = 0,95,
тогда:
по первому правилу:
p (1) = 0,9 ∙ 0,9 ∙ 0,95 ∙ 0,97 = 0,95 ∙ 0,81 ∙ 0,97 ≈ 0,75
по второму правилу:
p (1) = 0,9 ∙ 0,9 ∙ 0,75 = 0,81 ∙ 0,75 ≈ 0,6
по третьему правилу:
p(1) = 0,9 ∙ 0,95 ∙ 0,6 = 0,54 ∙ 0,95 ≈ 0,51
по четвертому правилу:
p(1) = 0,9 ∙ 0,95 ∙ 0,5 ≈ 0,43
Таким образом
p(1) = 0,75  (определяется по максимуму)

Примечание. Сравнивая данный материал с изложенным в 2.3, легко видеть, что для задачи распознавания почтовых индексов применение логических и продукционных моделей фактически идентично.