4.4.1. Понятие синтагматических цепей
В этой модели отражаются понятия и отношения (причем не только парадигмастические, но и меняющиеся со временем). Это позволяет описывать не только понятия, но и конкретные ситуации.
Синтагмой назовем выражение вида (x r y), где x, y – понятия или имена (понятия определяют целые классы объектов, а имена – конкретные экземпляры). r – отношение между понятиями или именами x и y. Понятия могут быть элементарными (первичными) или представлять собой другие синтагмы, образуя вложенность.
Пример. Опишем ситуацию. Автомобиль Волга с номером A364/70Rus движется по направлению к городу Томску.
Имеем четыре понятия: x1 – автомобиль, x2 – марка автомобиля, x3 – город, x4 – «Волга», два имени: i1 – A364/70RUS, i2 – Томск. А также четыре отношения: r1 – иметь имя, r2 – иметь признак, r3 – иметь значение, r4 – двигаться к.
Описание: Y1=((x1 r1 i1)r2(x2 r3 x4))r4(x3 r1 i2)
Синтагму можно представить в виде графа (рис. 4.3):
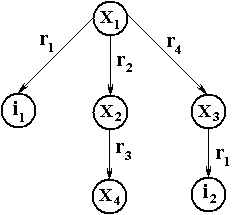
Рис. 4.3. Представление синтагматической цепи в виде графаПримечание. Любое отношение в естественном языке имеет обратное к себе, причем оба эти отношения имеют один и тот же смысл. Например, для отношения иметь имя, обратное – быть именем. Ориентация отношений чисто субъективный вопрос, однако она связана с формулировкой отношения.
В синтагматической цепи допустимо использование логических связок.
Пример. К городу Томску движется автомобиль Нива некрасного цвета. Вводим дополнительные понятия: x5 – Нива, x6 – цвет, x7 – красный.
Тогда ситуация Y2=((x1 r2 (x2 r3 x5)) r2 (x6 r3 x7)) r4 (x3 r1 i2).
Автомобиль Нива движется движется навстречу автомобилю №A364/70RUS: Вводим новое отношение R5 – двигаться навстречу.
Тогда ситуация Y3=(x1 r2 (x2 r3 x5)) r5 (x1 r1 i1)
Полностью ситуация, представленная в трех примерах описывается следующим образом: Y=Y1ÙY2ÙY3.
Можно также использовать и квантификаторы.
Пример. Почти всегда автомобиль, следующий из Томска в Кемерово, проезжает через Юргу.
Вводим квантификатор- почти всегда, имена: i3 – Тайга, i4 – Кемерово, отношения r6 – через, r7 – из.
Y4=(((x1 r7 (x3 r1 i2)) r4 (x3 r1 i4)) r6 (x3 r1 i3))
Примечание. В синтагматических цепях можно описать все элементы естественного языка, таким образом, это полный реляционный язык, соответственно дескрипторные языки и RX-коды не полны.4.4.2. Фреймы.
Рассмотрим выражение Y1 из примера в предыдущем пункте:
Y1=((x1 r1 i1)r2(x2 r3 x4))r4(x3 r1 i2)
Напомним, что таким образом описана ситуация «автомобиль Волга с номером A364/70Rus движется по направлению к городу Томску».
Подставим вместо имени i1 некоторую неизвестную переменную z1, тогда мы получим выражение, подразумевающее любую Волгу (номер cтанет не известен). Вместо i2 мы можем подставить переменную z2, тогда получим движение к любому городу. Если подставим переменную z3 вместо понятия x4, то получим автомобиль любой марки. Таким образом, получаем разные уровни фреймов. Переменные z1, z2 и z3 называются слотами, для каждого слота cуществует множество значений. Фреймы позволяют описывать общие случаи, а при подстановке вместо переменной конкретного понятия или имени конкретизируется ситуация.
Фреймовые модели очень широко применяются там, где следует автоматизировать процесс распознавания конкретной ситуации, прежде всего в системах ситуационного управления, т.е. в системах, которые просчитывают необходимое действие, поставленное в соответствие конкретной ситуации, которую следует распознать (пример – электронный диспетчер в аэропорту). На основе классических (неинтеллектуальных) методов построить такие системы фактически невозможно. Неэффективным оказывается и применение логических и продукционных моделей.
Отчасти с идей фреймов перекликается методология функционального программирования (самый распространенный функциональный язык – Лисп (Lisp) – list processor –n обработчик списков). Основные объекты Lisp-программы – список (содержит данные) и функция (вырабатывает конкретной результат). Программа практически представляет иерархию вложенных вызовов функций. Функциональное программирование и язык Лисп будут рассмотрены в восьмой главе.