Часто для построения требуемых ЭС недостаточно ЛППП. В этом случае находят применение более сложные модели, так называемые неклассические логики. Проведем краткий обзор этих логик.
2.4.1. Логики высших порядков.
В ЛВ кванторы отсутствуют вовсе, поэтому ее иногда называют логикой нулевого порядка. В ЛППП кванторы связывают переменные. В логики второго порядка сами предикаты могут быть связаны кванторами, и соответственно допускается вложенность предикатов.
"P(x) [Q (P(x), a) → S (b)]
В логике k-го порядка допускается вложенность предикатов глубины k, при этом предикаты глубины k-1 и менее могут быть связаны кванторами.2.4.2. Модальные логики.
Модальные логики представляют собой расширения ЛППП путем введения дополнительных элементов - квантификаторов (в отличии от кванторов, не связывающих переменные). В частности существуют.
A) Логика возможного.
,
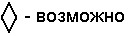
B) Логика веры .
,
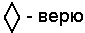
C) Логика времени
,

D) Другой вариант логики времени (добавляются также квантификаторы G – всегда в будущем, H -всегда в прошлом, F – иногда в будущем, P – иногда в прошлом).Другие логики.
Пример. Опишем на языке логики времени утверждение «иногда в прошлом рабочий день Сергея продолжался до 23 часов».
Введем предикат Q(x, y) - рабочий день x продолжается дон часов.
Тогда, P [Q(Сергей, 23)].
Модальные логики и логический вывод на модальных логиках, в настоящее время находят все более широкое применение.2.4.3. Многозначные логики.
В многозначных логиках высказывания и предикаты могут принимать не 2 значения (истина или ложь), а более. Существует множество таких логик, находящих все большое применение. Рассмотрим здесь трехзначную логику Лукашевича и четырехзначную логику параллельных миров (логику возможных миров).
В логике Лукашевича возможно три истинностных значения: 0 – ложно, 1 – возможно, 2 – истинно.
Используются дополнительные квантификаторы
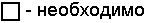
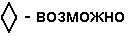
Таблицы истинности определены следующим образом: