Дескрипторные модели

Простейшие модели естественных языков – дексрипторные модели. В этих моделях отражаются только понятия и имена, которые в терминах модели называются дескрипторами.
Модель действительно очень проста: фраза на естественном языке моделируется простым перечислением дескрипторов, которые иногда называются ключевыми словами. Дескрипторная модель часто применяется в информационно поисковых системах (ИПС).

4.2.1. Понятие об ИПС.
Название этих систем говорит само за себя – это системы, предназначенные для поиска информации в документальных базах данных, в том числе в глобальных сетях, например, в Интернете. Практически всем широко известны следующие примеры ИПС: rambler, yandex, yahoo, google, hotbot и т.д.
Поиск в таких системах производится по некоторым ключевым словам, которые являются дескрипторами.
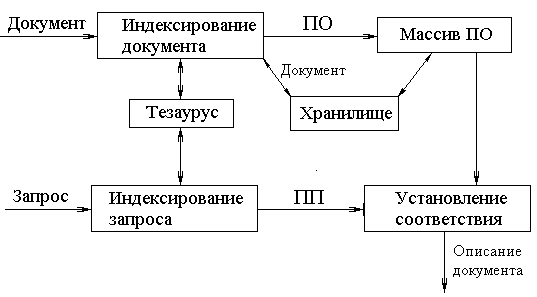
Структурная схема дескрипторной ИПС приведена на рис. 4.1

Рис. 4.1. Структурная схема дескрипторной ИПС

Здесь, ПО – поисковые образцы документов, ПП – поисковое предписание; и то и другое есть некоторый набор дескрипторов. Тезаурус содержит набор всевозможных дескрипторов, т.е. представляет собой массивный словарь. Хранилище содержит сам набор документов или ссылок на документы (ссылки используются при поиске в сетях), среди которых осуществляется поиск. При внесении документа в хранилище, вводится набор дескрипторов (ключевых слов), описывающих его. Набор ключевых слов помещается в тезаурус, а документ или его описание – в хранилище, связанное с массивом поисковых образцов (в нем для каждого документа хранятся ссылки на дескрипторы). При обработке запроса вводятся ключевые слова, на основе которых с использованием тезауруса формируется поисковое предписание. Далее происходит сверка поискового предписания с поисковыми образами, устанавливается соответствие и выдается документ или его описание, позволяющее найти документ. Методы сравнения поисковых образов и поисковых предписаний описаны в следующих пунктах данного параграфа.
Дескрипторной модели имеют два основных недостатка
A) Возможность ложной координации дескрипторов из-за неоднозначности понятий естественного языка. Например, дескриптор «ПРОЛОГ» может означать пролог к книге или одноименный язык программирования, дескриптор «ключ» – ключ от двери, родник, уникальный атрибут в реляционной таблице и т.д.
B) Неоднозначность из-за о.тсутствия определения ролей. Например, имеем фразу: «мать любит дочь». Возможно два толкования (грамматического разбора):

Иногда вводят в архитектуры систем возможности определения ролей, но в этом случае модель поиска уже не может называться дескрипторной, а механизмы поиска значительно усложняются.

4.2.2. Линейная модель работы ИПС.
Считаем, что в системе имеется t дескрипторов (иначе говоря объем тезауруса равен t). Тогда любой документ (точнее его поисковый образ)  можно идентифицировать с помощью битового (двоичного) вектора (x1,…..,xt), где xj=1, если j-й дескриптор присутствует в описании документа, в противном случае xi=0.
Если в системе d документов, то вся информация может быть представлена с помощью матрицы Cdt:

i-я строка матрицы является описанием i-го документа.

Запрос (точнее его поисковое предписание) также можно представить в виде битового вектора
- количество дескрипторов, которые одновременно присутствуют и в запросе и в i-м документе. Эта величина называется критерием релевантности i-го документа относительно запроса .
=(r1,….,rd) - вектор релевантностей для запроса .
Результатом поиска обычно признаются документы, релевантность которых выше заданного порога r*, который должен зависеть от числа дескрипторов в запросе и в документе, что не очень удобно.
Выражение для  можно записать в матричной форме: =C.
Пример. Пусть в системе имеется 6 дескрипторов и 2 документа имеющих описания (1,1,1,0,0,0) и (1,1,1,1,1,1). Подается запрос =(1,1,1,0,0,0). Тогда  r1=r2=3, хотя очевидно, что 1-й документ лучше соответствует запросу.
Другой критерий: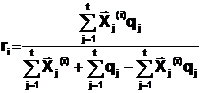  

Для нашего примера в этом случае r1=1, r2=1/2.
Как видим, второй критерий более совершенен, что объясняется учетом не только совпадений дескрипторов в описаниях, но и несовпадений.
К сожалению, в силу человеческого фактора, однотипные документы часто характеризуют разными ключевыми словами, и это необходимо учесть в поисковой модели. Целесообразно учитывать степень похожести дескрипторов и документов.
Вычислим матрицы A, D:
Att=СTtdCdt,    Ddd= CdtCTtd.
Элемент ajm матрицы A показывает количество одновременных присутствий j-го и m-го дескрипторов в описаниях документов, а элемент dik матрицы D– количество общих дескрипторов в i-м и k-м документах. Таким образом, матрица A показывает степень похожести дескрипторов, а матрица D – степень похожести документов. С помощью определения порогов a* и d* эти матрицы приводятся к бинарному виду:
Пусть:

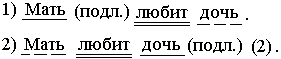
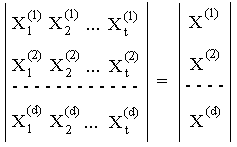
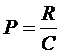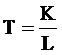aij ≤ a*=> aij'  = 0
aij > a* => aij = 1
dij ≤ d*=> dij'  = 0
dij > d* => dij = 1

Имеем смысл использовать критерий:
R=D'(C (A' Q))
Фактически в этом случае все похожие дескрипторы автоматически добавляются к запросу, по расширенному запросу производится поиск, а затем к множеству полученных документов добавляются похожие.

4.2.3. Понятие о многоуровневом поиске
Основной причиной отсутствия возможностей применения линейной модели в крупных ИПС является очень большое количество понятий в естественных языках, вследствие чего матрицы разрастаются до таких размеров, что мощности ЭВМ не хватает, чтобы выполнять их обработку. В связи с этим на практике в универсальных ИПС применяются различные варианты многоуровневого поиска.
Для двухуровневого случая выбираются группы похожих документов с помощью неприведенной матрицы D и создаются описание для групп документов. А внутри каждой группы уже описывается сам документ. Поиск осуществляется в 2 этапа: сначала ищется нужная группа документов, а затем внутри этой группы сам документ. Очевидно, что уровней иерархии может быть сколько угодно, различными могут быть и принципы разделения на группы.

4.2.4. Основные характеристики ИПС
Основными характеристиками ИПС являются полнота и точность поиска.
Полнота поиска выражается отношением

,

где С – число подходящих документов, R – число таковых документов, выданное системой.
Точностью поиска называется отношение

,

где L – число документов, выданных системой, а K – число таковых документов, действительно соответствующих запросу.
На практике полнота, как правило, обратно пропорциональна точности.