Сетевые модели представления знаний

Сетевые модели – частный случай реляционных. В естественном языке понятия связаны некоторыми отношениями. Эти отношения на самом деле не являются разрозненными, а образуют некую единую сеть взаимосвязей, которая отражается в сетевых моделях. Иногда к сетевым причисляют формы представления знаний, не относящиеся к реляционным языкам, но предполагающие структуризацию в виде сети (например, нейронные сети).

4.5.1. Понятие семантической сети
Начнем с неформального определения. Под семантической сетью понимается простой ориентированный граф, вершины которого соответствуют понятиями (или именами) естественного языка и помечены знаками соответствующих понятий, а ребра соответствуют отношениям между ними и помечены знаками соответствующих отношений.
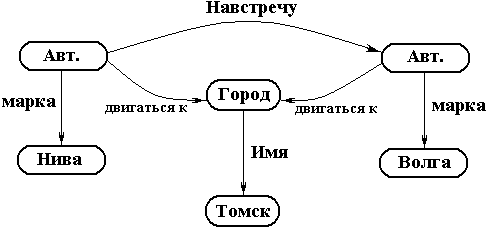
Пример 1. Автомобили Нива и Волга движутся навстречу друг к другу по направлению к городу Томску.
Семантическая сеть, соответствующая данному примеру представлена на рис. 4.4.

Рис. 4.4. Семантическая сеть

Теперь приведем формальное определение. Семантической сетью называется пятерка ((X, O), A, R, f, g),
где  (X,0) – простой ориентированный граф (X – множество вершин, O – множество ребер, т.е. фактически упорядоченных пар вершин),
A – множество понятий и имен,
R – множество отношений,
f: X→A – функция разметки вершин (каждой вершине ставится в соответствие одно и только понятие),.
g: O →  функция разметки ребер (каждому ребру ставится в соответствие непустое подмножество понятий).
Семантические сети часто используются при решении задач распознавания образов (сюда относятся  задача распознавания печатных знаков, распознавание звуков человеческого голоса и т.д.).
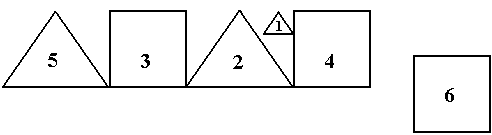
Пример 2. Пусть есть следующее изображение (рис. 4.5.):

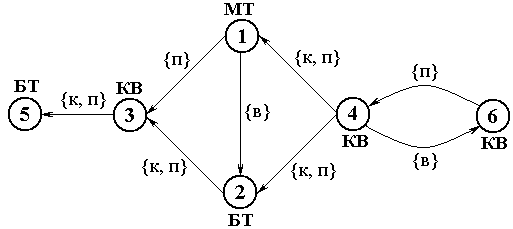
Рис. 4.5. Изображение.

Его можно смоделировать с помощью следующей семантической сети (рис. 4.6.):

Рис. 4.6. Семантическая сеть.

Здесь, А={КВ, МТ, БТ}, R={в, к, п}.
КВ – квадрат, МТ – малый треугольник, БТ – большой треугольник, в – выше, к – касаться, п – правее.
В виде семантической сети можно представить не только исходные данные, но и запрос. Задача состоит в том, чтобы определить имеется ли в исходной сети фрагмент, соответствующий запросу и если таковой имеется, то выделить его.
Алгоритмы поиска в семантической сети применимы и в ИПС.

4.5.2. Структура интеллектуальной системы доступа к данным на основе семантической сети.
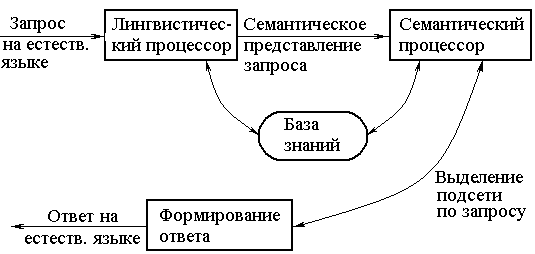
Так называемая, интеллектуальная система доступа к данным, по сути, является разновидностью ИПС. Ее структурная схема дана на рис. 4.7..
.

Рис. 4.7. Структура интеллектуальной системы доступа к данным

База знаний хранится  в виде массивной семантической сети. Блоки формализации запросов и формирования ответов основаны на приближенных моделях естественных языков, либо отсутствуют вовсе ( в этом случае запрос формируется пользователем в виде семантической сети).

4.5.3. Задача поиска кратчайшего обхода образца в семантической сети.
Семантическая сеть ((X1, O1), A1, R1, f1, g1) называется подсетью семантической сети ((X, O), A, R, f, g), если
A) X1  X, O1  O (множества вершин и ребер подсети являются подмножествами соответствующих ребер сети);
B) "xi, xjX1 [((xi, xj)O)→((xi, xj)O1)] (если две вершины, присутствующие в подсети соединены ребром в сети, то это ребро присутствует и в подсети);
С) "xiX1 f1(xi)=f(xi) (в подсети сохраняется разметка вершин);
D) "(xi, xj)O1 g1((xi, xj))=g((xi, xj)) (в подсети сохраняется разметка ребер).
Примечание. Из определения видно, что подсеть фактически можно задать подмножеством вершин, т.к. ребра и разметка сохраняются.
Запрос к семантической сети представляется также в виде семантической сети.
Пример. Какие фигуры находятся правее и касаются квадрата, находящегося, в свою очередь, правее и касающегося треугольника.

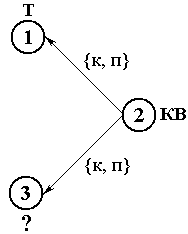
Рис. 4.7. Запрос

Формально вводится отображение φ(a):a - > P(A) , которое задает множество суперпонятий, например
T→{МТ, БТ}, ГФ→{КВ, МТ, БТ},
т.е. понятию «Т» (треугольник) соответствуют понятия MT (малый треугольник) и БT (большой треугольник), все квадраты и треугольники соответствуют понятию «ГФ» (геометрическая фигура).
Процесс поиска сводится к тому, что запрос (образец) отображается в семантическую сеть, и производится поиск всех образов (подсетей), по которым и определяется ответ.
Отображение hY: X1→X2 называется частичным изоморфизмом семантической сети ((X1, O1), A1, R1, f1, g1) на семантическую сеть ((X, O), A, R, f, g) с критериальным множеством YX, если для "xi, xjX1 выполняются следующие условия:
A) (xi, xj)O1 => (hY(xi), hY(xj))O (каждому ребру в исходной сети должно соответствовать ребро в образе);
B) f1(xi)<>a0 => f(hY(xi))φ(f1(xi)) ( a0 – это вершина, помеченная вопросом, остальные вершины должны задавать некие суперпонятия, которые должны содержать по крайней мере те понятия, которыми помечены их образы);
С) g1(xi, xj) g(hY(xi), hY(xj)) (если в исходной сети ребро помечено некими метками, то соответствующее ребро в образе должно содержать, по крайней мере, те же метки);
D) Если xi, xjYX1 => [(hy(xi)=hy(xj))→(xi=xj)]. (разные вершины исходной сети, принадлежащие критериальному множеству Y отображаются в разные образы).
Подсеть называется релевантной образцу по критерию hY, где hY – отображение образца на семантическую сеть, если hY является частичным изоморфизмом.
Однако иногда требуется не просто выделить релевантную образцу подсеть, а установить соответствие между маршрутами, которые могут описывать конкретные ситуации.
Неформально под маршрутом в семантической сети называется последовательность типа вершина-ребро-вершина и т.д., каждое из которых называется звеном, причем звенья могут быть как положительной, так и отрицательной ориентации. Изображением маршрута называется последовательность пометок вершин и ребер, входящих в маршрут. Поскольку на ребре может быть несколько пометок, то у одного и того же маршрута может быть несколько изображений. Для ребер отрицательной ориентации в изображении предусмотрена специальная пометка T.
Пример маршрута и изображения
маршрут
1 -4 – 6 + 4 + z
изображение 1
МТ кТ  КВ пТ КВ п КВ п БТ
изображение 2
МТ кТ КВ вТ КВ п КВ к БТ
Полным обходом образца называется маршрут в образце, проходящий по каждому ребру столько раз, сколько пометок на ребре. Изображением полного обхода образца называется изображение соответствующего ему маршрута такое, что для каждого ребра каждая пометка встречается хотя бы один раз.

Пример.
2 + 3 – 2 + 1 – 2  - полный обход образца,
КВ к ? пТ КВ п Т кТ КВ – изображение полного обхода образца.
Говорят, что подсеть релевантна образцу в соответствии с критерием hp (hp – отображение), если одно из изображений одного из маршрутов в подсети покрывается изображением полного обхода образца. Под покрытием в данном случае понимается, что пометки ребер в изображениях совпадают, а пометкам вершин должны соответствовать либо аналогичные пометки, либо пометки, являющиеся подпонятиями соответствующих суперпонятий.
Пример.
КВ к ? кТ КВ п Т пТ КВ
//полный обход образца и покрываемый им маршрут
Доказана следующая теорема. Если некоторая подсеть релевантна образцу в соответствии с критерием hp, то она релевантна ему и в соответствии с критерием hY, при пустом критериальном множестве (Y=ǿ (20) ) .
С точки зрения эффективности выгоднее искать не какой-то произвольный обход образца, а кратчайший из них по количеству ребер. Алгоритм построения такового здесь не рассматривается из-за его сложности.

4.5.4. Понятие о логическом выводе на семантических сетях.
Часто существуют отношения, в явном виде не заданные в сети, часто вместо отношения задана его редукция. Под редукцией здесь понимается решение уравнения   R = R+, где R+ – положительное транзитивное замыкание отношения.
Такая ситуация связана с тем, что, во-первых, пользователю просто физически тяжело выявить все отношения, а во-вторых, семантические сети на практике и так достигают очень больших размеров, что дальнейшее требование памяти становится неприемлемым. Человек в повседневной жизни практически никогда не хранит информацию обо всем, то он может ее восстановить, пользуясь причинно-следственными связями. Так математик зачастую вроде бы помнит наизусть сложные доказательства, но на самом деле он помнит не текст доказательства, а его внутреннюю логику. Существует смысл и семантические сети научить восстанавливать связи, неуказанные в явном виде.
Будем считать, что отношения могут быть:

Идея восстановления состоит в том, чтобы хранить логические  правила, справедливые для отношений, тогда можно воспользоваться системой автоматизированного логического вывода.
Пример. Отношение правее.
((X n y) Ù (y n Z))  => (X n Z)
Опишем проблему с формальной точки зрения.  Пусть имеется некоторая теория T, содержащая множество аксиом типа riÙrj→rk. Будем считать, что вершины x и z семантической сети связаны эксплицитным отношением rk, если в сети  существует маршрут  и в теории T может быть доказана теорема .
Обычно используется логика высказываний, в которой скорость вывода значительно выше, чем в ЛППП.
На первый взгляд эта модель кажется универсальной. На самом деле все же возникают значительные трудности.
A) Пользователю нелегко задать все логические правила.
B) Любая формальная теория, в том числе и теория T, неполна в соответствии с теоремой Геделя, т.е. неизбежны случаи, когда существование эксплицитного отношения будет невозможно ни доказать, ни опровергнуть.